Numbers, units and arithmetic
Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Saturday, 20 April 2024, 1:34 AM
Numbers, units and arithmetic
Introduction
This free course, Numbers, units and arithmetic, will help you to revise whole numbers, decimals and fractions, both positive and negative. You should know when and how to add, subtract, multiply and divide. Although you may have a calculator, you still need to do simple calculations in your head or on paper. Such calculations could be to estimate the size of an answer, as a check for your calculator work.
This OpenLearn course provides a sample of level 1 study in Mathematics.
Get careers guidance
This course has been included in the National Careers Service to help you develop new skills.
Learning outcomes
After studying this course, you should be able to:
- write whole numbers and decimals in place-value columns and compare their sizes
- multiply and divide whole numbers and decimals by 10, 100, 1000 and so on
- indicate given fractions on a diagram and find equivalent fractions for a given fraction
- mark numbers on a number line
- choose appropriate units for a given purpose.
1 The size of numbers
Numbers are used to specify a quantity or amount. For example, people give their ages as a number of years: ‘I am 51 years old’ or ‘I am five and a half’. Votes in elections may be described in thousands. Temperatures are measured in positive and negative degrees Celsius. Numbers smaller than one may be expressed as fractions or decimals. This section considers whole numbers, decimals, fractions and negative numbers and reminds you of the essence of a number – how ‘big’ it is.
1.1 Whole numbers
Whole numbers arise from counting: for example the number of sheep in a field or the number of votes in an election.
Our everyday number system is the decimal system, where the position of a digit within the number determines whether it represents units, tens, hundreds, thousands etc.
For example, the number 1375 means one thousand three hundred and seventy-five. The position of the 3, third from the right, means that it represents 3 hundreds.
A thousand thousand, 1 000 000, is called a million and a thousand million, 1 000 000 000, is called a billion. (A British billion used to be a million million, but now the US convention of a thousand million is normally used.) To compare two numbers, it sometimes helps to write them, or think of them, in columns:
| Millions | Hundred Thousands | Ten Thousands | Thousands | Hundreds | Tens | Units |
The position of a digit in the columns is called its place value.
Example 1
A lottery organiser announces that this week’s winnings will be over two million pounds. After the draw, the organisers announce that the winnings were £2 201 995. Was the announcement correct?
The issue is whether the figures represent a number greater than two million, or not. Write the two numbers in a number column table. Start with two million.
Answer
| Millions | Hundred Thousands | Ten Thousands | Thousands | Hundreds | Tens | Units |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 0 | 1 | 9 | 9 | 5 |
Now look at the numbers from the left. Both numbers have a 2 in the millions column, so move to the next place. The first number has a 0 in the next column (i.e. hundred thousands) whereas the second number has a 2. So the second number is larger, the announcement was correct and more than two million pounds was paid out.
In practice you probably won’t want to write the headings in the columns each time. But do keep their meanings in mind.
Try some yourself
Activity 1
Can you answer the following questions:
(a) Write ‘twenty thousand one hundred and forty-four’ as a number.
(b) Say (or write) the number 31 002 103 in words.
Answer
Your answers should be
(a) The number is 20 144 (or it could be written 20,144).
(b) Thirty-one million two thousand one hundred and three.
1.2 Using the place value
Writing numbers in place-value columns gives an easy way of multiplying by 10, 100, 1000 and so on. Have a look at the place value table again.
| Millions | Hundred Thousands | Ten Thousands | Thousands | Hundreds | Tens | Units |
Notice that moving all the digits one column to the left in the table (and adding a zero to the units column) is the same as multiplying by ten; for instance, ten tens are a hundred, ten hundreds are a thousand. If you move two columns to the left, you multiply by a hundred; for instance, a hundred tens are a thousand. Moving three columns to the left is equivalent to multiplying by a thousand, and so on.
Example 2
After local government re-organisation a new council expects to receive cash payments in ten instalments from about 26 000 households. In order to negotiate the cash collection at post offices it needs to know how many payments are made altogether in a year. How many are there likely to be?
Answer
The total number of payments is the number of households times the number of payments per household, i.e. 26 000 × 10. This can be worked out by moving all the digits of 26 000 one place to the left, and adding a zero at the end:
| M | H Th | T Th | Th | H | T | U | ||
| 2 | 6 | 0 | 0 | 0 | ||||
| = | 2 | 6 | 0 | 0 | 0 | 0 | ||
| Digits moved one place to the left | Extra zero added | |||||||
So 26 000 × 10 = 260 000.
A total of 260 000 cash payments should be expected.
Try some yourself
Activity 2
Write each of the following three numbers in numerals and then place them in ascending order:
eight hundred and eight thousand
two million and twenty-four
nine thousand nine hundred and ninety-eight
Answer
Written in numerals, the numbers are:
808 000, 2 000 024, 9 998
So, in ascending order, we have:
9 998, 808 000, 2 000 024.
Activity 3
Multiply 2490 by 100.
Answer
2490 × 100 = 249 000
Notice that the digits have moved 2 places to the left and two zeroes have been added at the right.
Activity 4
Now try to answer these questions:
(a) Place the following numbers of votes in an election in order, with the smallest first:
9 999, 5 001, 49 020
(b) Multiply 9 494 by 100.
Answer
Your answers should be:
(a) 5 001, 9 999, 49 020.
(b) 949 400.
1.3 Number lines
It is often useful in mathematics to think of numbers stretched out along the imaginary number line. The diagram below shows part of the number line.
As you move to the right along the number line, the numbers increase.
This concept will be useful for picturing other numbers, as well as whole numbers.
1.4 Decimals
Quantities can be smaller than one (such as 0.5 kg) or take values between whole numbers (such as a height of 1.65 metres). Numbers smaller than one are expressed as decimals or as fractions. Decimals are often easier to work with (especially when using a calculator). Decimals are explained in this section, and fractions following that (Section 1.7).
Decimals can be indicated on the number line in between whole numbers. 0.5 and 1.65 are indicated on the figure below.

Decimals arise when whole numbers are divided by ten, a hundred etc.
Example 3
What is 3579 cents in dollars? (There are 100 cents in a dollar ($).)
Answer
You need to divide 3579 by 100. To multiply a number by 100, you shift the digits two places to the left (and add zeros to fill the spaces). To reverse the process, i.e. to divide by 100, move the digits two places to the right. To show this, you need to mark the end of the units column, and this is done by means of a decimal point.
| Th | H | T | U | |||||
| 3 | 5 | 7 | 9 | |||||
| = | 3 | 5 | 7 | 9 | ||||
| Digits moved two places to the right | ||||||||
So the answer is 35.79, or in words, thirty five point seven nine (not seventy nine).
So 3579 cents = $35.79.
Try some yourself
Activity 5
When dividing by 1000, move the digits 3 places to the right (past the decimal point). Divide 202.15 by 1000. What is 202.15 metres in kilometres?
Answer
0.20215. So 202.15 metres are 0.20215 kilometres.
1.5 Decimals and place value
What do the digits to the right of the decimal point mean? The first column to the right of the decimal point is obtained by dividing the units by 10; this is the ‘tenths’ column. Similarly the next column contains the hundredths, and so on. So here is the extended place value table:
| ... | Thousands | Hundreds | Tens | Units | Tenths | Hundredths | Thousandths | ... |
A tenth is 0.1 or 1 divided by 10, i.e. .
A hundredth is 0.01 or 1 divided by 100, i.e. .
A thousandth is 0.001 or 1 divided by 1000, i.e. .
So 0.101 is one tenth plus one thousandth or .
Notice that you need to include the zeros after the decimal point in numbers like 0.05 or 0.005, just as you do before the decimal point in numbers like 50 or 500, in order to indicate the place value of the 5. Also, note that often there is a 0 before the decimal point for numbers smaller than one. Whether it is written as 0.1 or .1 the value is still the same (one tenth). 0.1 is more usual when writing, .1 is more usual on calculators. In general, adding the zero before the decimal point is a clearer way of writing the number – the decimal point will then not be missed.
Example 4
Two people go to a ‘pick your own’ orchard and gather a large bag of apples each. They weigh the bags and find the first weighs 6.85 kg and the second weighs 6.58 kg. Which is heavier?
Answer
The point at issue is which number is larger, 6.85 or 6.58. To determine this, write the digits in a place value table and then compare the values in each column:
| Units | Tenths | Hundredths | |
| 6 | 8 | 5 | |
| 6 | 5 | 8 |
Again, work from the left. The digits in the units column are the same, so look at the next column. The first number has 8 tenths and the second number has 5 in this column (5 tenths), so the first number is bigger which means that the first bag is heavier.
Try some yourself
Activity 6
What is 370.76 grams in kilograms? There are 1000 grams in a kilogram.
Answer
370.76 ÷ 1000 = 0.37076.
So 370.76 g = 0.37076 kg.
Activity 7
Place the following numbers of kilometres in order, with the smallest distance first:
1.013 1.103 1.0103 1.0129
Answer
Writing the numbers out in columns with the decimal points lined up (as in a place value table), gives:
1.013
1.103
1.0103
1.0129
Working from the left shows that 1.0103 is the smallest, follwed by 1.0129. So in ascending order they are:
1.0103, 1.0129, 1.013, 1.103.
Activity 8
Place the following measurements in ascending order:
0.1704 metres 0.1074 metres 0.0714 metres 0.0741 metres
Answer
Writing the numbers out in columns with the decimal points lined up (as in a place value table), gives:
0.1704
0.1074
0.0714
0.0741
Working from the left, shows that 0.0714 is the smallest, followed by 0.0741. So in ascending order (in metres) they are:
0.0714, 0.0741, 0.1074, 0.1704.
1.6 Fractions
A fraction is written as one number over another (such as ) and means the top number divided by the bottom number. The top number, 3, is called the numerator and the bottom number, 10, is called the denominator. Whole numbers can be written as fractions with the denominator 1. Thus, 2 can be written as . The same fraction may be written in different ways, depending upon the context.
The top of a fraction is called the numerator.
The bottom of a fraction is called the denominator.
Click on the tabs below and note that all of the shaded areas represent the same fraction of the circle: one third of it. So
Fractions which are equal in value but are written with different numerators and denominators are called equivalent fractions.
You can find equivalent fractions for any given fraction by multiplying top and bottom by the same whole number.
Decimals are themselves a special form of fractions (0.3 is ). There are situations where it is simpler to use fractions. For example, if you wanted to divide a circle into six equal pieces, you think of the fraction . There is no exact decimal equivalent of (because dividing 6 into 1.0000 … produces a never-ending string of 6s: 0.1666 …). Recipes often ask for fractions, such as ‘half a pint of milk’ or a cooking time of ‘three-quarters of an hour’.
Example 5
What fraction of the circle is shaded in the diagram below?
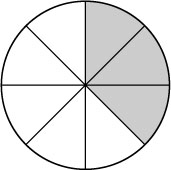
Answer
The fraction is . The circle is divided into 8 equal sections, so each section is . Three of them are shaded so the shaded part is of the circle.
However there are other equivalent fractions which represent the same shaded area, obtained by multipying the numerator and the denominator by the same whole number, e.g. .
Try some yourself
Activity 9
The diagram below shows an oatmeal cake marked into 12 equal portions. I want to give my sister a third of the cake. Where could I cut the cake, and what would be left over?
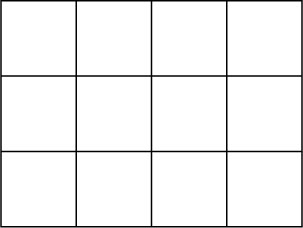
Answer
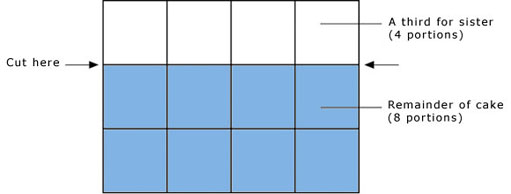
(There are several other ways of cutting the cake into one-third (4 portions) and two-thirds (8 portions).)
Activity 10
Which two of the following fractions are equivalent to each other?
Answer
Only and are equivalent fractions, since .
(Notice that neither , which is , nor , which is , are equivalent to .)
1.7 Simplest form of a fraction
The fraction , is the simplest form of all its equivalent fractions, because it cannot be ‘simplified’ further (by dividing top and bottom by the same whole number called a common factor); or , on the other hand, can be simplified to by dividing top and bottom by 2 and 4 respectively.
A fraction is in its simplest form if the numerator and the denominator have no common factors.
6 can be written as 2 × 3. 2 and 3 are called factors of 6.
15 can be written as 5 × 3. 5 and 3 are factors of 15.
3 is a common factor of 6 and 15. Hence . This is the simplest form of .
Example 6
(a) Find some equivalent fractions for .
(b) What is the simplest form of ?
Answer
Multiply or divide top and bottom by the same whole number to give an equivalent fraction.
(a) Some examples are
(b) Top and bottom are divisible by 5. So
3 and 4 have no common factors so is the simplest form.
You can indicate fractions along the number line by marking points between the whole numbers. The numbers and are shown below.

Note may also be written as 1.5 or as .
Try some yourself
Activity 11
For each of the following shapes, indicate the fraction of the whole shape represented by the shaded parts:

Answer
(a) 1 part is shaded out of 4 (equal parts). So the fraction is
(b) 7 parts are shaded out of 12 (equal parts). So the fraction is
(c) 3 parts are shaded out of 7 (equal parts). So the fraction is
1.8 Negative numbers
Numbers can be positive or negative, i.e. greater than or less than zero. Negative numbers have several uses; for example, to measure temperatures below zero, such as −3°C (‘minus 3 degrees Celsius’). They are also used to represent debts and overdrawn accounts: a bank balance of −£84.33 means ‘overdrawn by £84.33’.
Negative numbers are shown on the number line to the left of 0. The animation below shows −8, −7, −6, etc.
The numbers always increase as you move to the right along the number line, wherever you start from. 1 is to the right of −2, so 1 is greater than −2. 1° is warmer than −2° and a bank balance of £1 is more than one of −£2 (two pounds overdrawn).
Try some yourself
Activity 12
Copy the number line below, and mark the following points on your copy:
Answer

Activity 13
What are the numbers marked A, B and C on the number line below?

Answer
A is (or −1.6),
B is (or −0.6),
C is (or 1.2).
1.9 Negative number notation
It is worth mentioning notation at this point. You may have noticed that the minus sign used to denote a negative number is shorter, closer to the number and raised, compared with the minus sign used to denote subtraction. It is important to distinguish between the two, and it can help to think of −3, say, as ‘negative 3’ rather than ‘minus 3’. In the calculation 8 − 3 (8 subtract 3), the minus sign is an operator, an instruction to subtract; in −3, the sign is part of the number. The two types of minus sign are distinguished on many calculators. If you have a calculator handy, look at the key pad to see if you have two keys. They are often labelled ![]() and
and ![]() .
.
Try some yourself
Activity 14
Contour lines on a map show all the points at a given height above sea level. The lines are drawn for each height at 50-metre intervals, and points below sea level are shown by negative heights. The diagram below shows a peak with six such contour lines. The lines for −100, 0 and 100 have been labelled. Copy the diagram and label the other three contour lines.
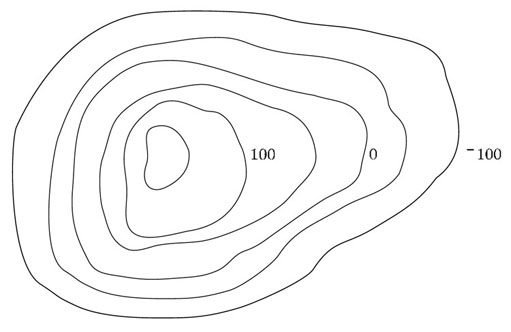
Answer
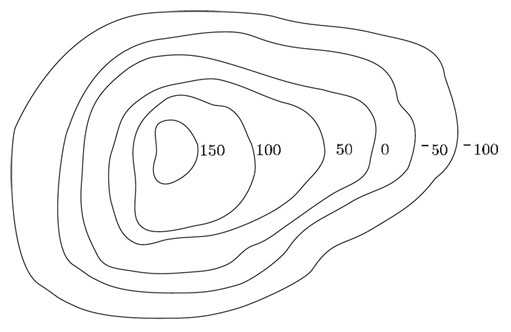
You might like to make some notes on this section before moving on to the next section.
2 Units of measurement
Numbers are used to count things (such as 54 sheep in a field) or, together with units of measurement, to quantify something (such as a 2-litre water bottle or a 3-year waiting list for an operation). This section reminds you of some units of measurement and considers appropriate units to use. We also need to make comparisons between quantities given in different units.
2.1 Which units to use
It is important to choose appropriate units, both to have a sense of the size you are talking about and also to avoid having to deal with very large or very small numbers.
For example using the UK decimal system, where £1 = 100p (one pound is equivalent to 100 pence), you would probably use pence for prices less than a pound: 50p rather than £0.50 and pounds for larger amounts, e.g. £2.50 instead of 250p.
For distance, mass and liquid measures, the metric system of units is often used. For example, the distance a cyclist cycles in a day is likely to be given in kilometres (sometimes written as the symbol km), a person’s height in metres (m) and a waist measurement in centimetres (cm). The prefixes ‘kilo’ and ‘centi’, together with ‘deci’ and ‘milli’, are used throughout the metric system. Some common prefixes are shown in Table 1.
| Prefix | Symbol | Meaning | Factor |
|---|---|---|---|
| micro- | μ | one millionth | 0.000001 |
| milli- | m | one thousandth | 0.001 |
| centi- | c | one hundredth | 0.01 |
| deci- | d | one tenth | 0.1 |
| kilo- | k | thousand | 1000 |
| mega- | M | million | 1 000 000 |
| giga- | G | thousand million | 1 000 000 000 |
So 1 centimetre = metre or 1 cm = m.
This is the same as saying there are 100 centimetres in 1 metre or 100 cm = 1 m.
For mass, kilograms (kg), grams (g) or milligrams (mg) are usually used and a metric tonne is used for very large masses (1000 kg). The word ‘mass’ is scientifically more precise than ‘weight’, although people usually talk about weight rather than mass. For liquid capacity, litres (l), decilitres (dl), centilitres (cl) or millilitres (ml) are used.
Units in action
Example 7
Imagine a friend is planning a new kitchen in her house. In the kitchen showroom she noticed that the measurements of most of the kitchen units were given in millimetres. One worktop, for instance, is 575 mm deep. What units should she use to measure the large room in the house where the new kitchen will be located?
Answer
She could measure in millimetres, but that would give large numbers. It is difficult to visualise the room in terms of millimetres – 1 mm is approximately the thickness of a piece of wire. Can you imagine how many of those would fit along one wall! But thinking of it in terms of metres may be easier. A single bed is about one metre wide so you could visualise how many would fit side by side along each wall. This will help check measurements. So she might measure each side of the room in metres (e.g. 2.82 m by 4.25 m). To avoid using decimals, she could have used centimetres instead (giving 282 cm by 425 cm). Either of these would be sensible. It would be unhelpful (to say the least!) to quote the dimensions in kilometres (e.g. 0.00282 km by 0.00425 km).
Try some yourself
Activity 15
Suggest appropriate units for each of the following:
(a) the age of the kitten when it is weaned;
(b) the distance between one train station and the next;
(c) the amount of one ‘active’ ingredient of a prescribed pill;
(d) the cost of leaving the light on continuously for 24 hours.
Answer
(a) The age of a young kitten would be measured in weeks or days.
(b) The distance between train stations could be measured in kilometres (or miles).
(c) The active ingredients of a pill are usually measured in milligrams.
(d) The cost of leaving a light on for 24 hours will vary according to the type of bulb and the price of electricity, but it is likely to be measured in pence.
Activity 16
Choose appropriate units for each of the following, using metric units where possible:
(a) your height;
(b) your weight;
(c) the length of time to boil an egg;
(d) the capacity of a large pan.
Answer
(a) Your height could be measured in metres, e.g. 1.55 m, or centimetres, e.g. 155 cm. It may be that you only know your height in feet and inches, e.g. 5 ft 1 in.
(b) Your weight might be given in kilograms, e.g. 58.06 kg, or perhaps in stones and pounds, e.g. 9 st 2 lb.
(c) The length of time to boil an egg is usually given in minutes, e.g. 3 min.
(d) Pans are described in terms of the amount of liquid they hold, measured in litres (or pints), e.g. a 2‑litre pan.
2.2 Converting units
A great advantage of the metric system of units is that conversion between units within the system is particularly easy. For example, ‘£1 is worth 100p’ is converting one pound into pence. To convert pounds to pence, you multiply by 100. So £2 is 200p, and £2.63 is 263p. (Remember that to multiply by 100, you move the digits two places to the left in the place value table.)
To convert from pence to pounds, you need to reverse this process, i.e. to divide by 100 (moving the digits two places to the right) so that 845p becomes £8.45. In the same way, any of the metric units can be converted simply by multiplying or dividing by ten, a hundred or a thousand. For example, the statement ‘1 m = 1000 mm’ tells you that to convert from metres to millimetres you multiply by 1000.
The general rule when converting units is: to convert from a larger unit (e.g. metres) to a smaller one (e.g. millimetres), multiply; to convert from a smaller unit to a larger one, divide.
Example 8
The measurements of the kitchen units in the example above were given in millimetres – a unit was 575 mm deep. What is this in metres?
Answer
To convert millimetres to metres, divide by 1000. So to convert 575 mm to metres, move the digits three places to the right:
575.0 ÷ 1000 = 0.575.
So the answer is 0.575 m.
There is no handy metric system for time. There are 60 seconds in a minute, 60 minutes in an hour, 24 hours in a day and 7 days in a week; a month may be 28, 29, 30 or 31 days long and a year may contain 365 or 366 days.
Try some yourself
Activity 17
A person’s height is given as 1.65 m. What is this in centimetres?
Answer
1.65 m is 165 cm (multiply by 100).
Activity 18
Try the following conversions:
(a) Express 675 mm in centimetres.
(b) Express 45.2 km in metres.
(c) Express 3.5 kg in grams.
(d) Express 167.2 mm in metres.
Answer
(a) To convert millimetres to centimetres, divide by 10. So 675 mm is 67.5 cm.
(b) 45.2 km is 45 200 m (multiply by 1000).
(c) 3.5 kg is 3500 g (multiply by 1000).
(d) 167.2 mm is 0.1672 m (divide by 1000).
Activity 19
A kitchen unit is 1200 mm long, 600 mm high and 350 mm deep. Write these measurements in metres.
Answer
To convert millimetres to metres, divide by a thousand, i.e. move the numbers three places to the right in the place value table. In terms of metres, the kitchen unit is then 1.2 m long, 0.6 m high and 0.35 m deep.
We will now provide more detail on converting units using interactive activities.
2.3 Measuring mass
The basic SI unit for mass is the kilogram, symbol kg
The tonne (t) which is equivalent to 1000 kg and is a metric unit is often used alongside the SI units.
The animation below illustrates how to convert between the most commonly used units of mass, the metric tonne (t); the kilogram (kg); the gram (g); the milligram (mg) and the microgram (μg).
For example, to convert 480 kg into t, divide by 1000.
So 480 kg = 480 ÷ 1000 t = 0.48 t.
Try some yourself – use the calculator to type in the amount and then choose the units you want to convert. Then choose the operation (multiply or divide) and the factor. Then select check to see if your answer is correct.
2.4 Measuring length
The basic SI unit for length is the metre, abbreviation m.
The animation below illustrates how to convert between the most commonly used units of length, kilometres (km); metres (m); centimetres (cm); millimetres (mm) and micrometres (μm).
For example, to convert 6.23 km into cm, multiply by 1000 to convert into m, and then mulitply by 100 to convert the measurement into cm.
So 6.23 km = 6.23 × 1000 m = 6230 m = 6230 × 100 cm = 623 000 cm.
Try some yourself – use the calculator to type in the amount and then choose the units you want to convert. Then choose the operation (multiply or divide) and the factor. Then select check to see if your answer is correct.
2.5 Measuring capacity
The basic metric unit for capacity is the litre, usually denoted by the symbol l (though sometimes an uppercase L is used to avoid confusion with the number 1).
In the SI system, units such as cubic metres (m3), cubic centimetres (cm3) and cubic millimetres (mm3) are used. These two systems are linked because:
1 ml = 1 cm3
The animation below illustrates how to convert between the most commonly used units of capacity:
Notice that to convert cubic centimetres to cubic millimetres, you need to multiply by 1000, NOT 10. To see this, imagine that you have a box which has internal measurements 1 cm by 1 cm by 1 cm. So, its volume is 1 cubic centimetre.
Now imagine filling it with tiny cubes, each side of which was 1 mm, so the volume of each tiny cube is 1 mm3. You would be able to fit 10 rows each with 10 tiny cubes in the bottom of the box, that is 100 tiny cubes altogether.
But these cubes would only fill the depth of the box to 1 mm. So you would be able to get 10 layers (each with 100 tiny cubes) into the box overall.
So there would be 1000 tiny cubes in the box.
In other words 1 cm3 = 1000 mm3.
Can you explain why 1 m3 = 1 000 000 cm3?
The argument is similar to that above for cm3 and mm3, except that there are 100 cm in a m, so a cubic metre (a 1 m by 1 m by 1 m cube) has 100 by 100 by 100 little cubic cm in it.
Example 9
Convert 500 cm3 into litres.
Answer
To convert 500 cm3 into l, divide by 10 to convert into cl, and then divide by 100 to convert the measurement into l.
So, 500 cm3 = 500 ÷ 10 cl = 50 cl = 50 ÷ 100 l = 0.5 l.
Try some yourself – use the calculator to type in the amount and then choose the units you want to convert. Then choose the operation (multiply or divide) and the factor. Then select check to see if your answer is correct.
2.6 Comparing measurements
In order to compare quantities, it is best to express them in the same units.
Example 10
Three children have just measured their own heights in metric units. Isaac says ‘My height is 1098’, Jasmine says ‘My height is 112’ and Kim says ‘Mine is 1.1’. What units were they using? Who is the tallest?
Answer
First decide what units the children were using and then convert all the measurements to the same units. It is reasonable to guess that the heights are between 1 and 2 metres. (A height between 10 cm and 20 cm would mean they were not yet born, whereas a height between 10 m and 20 m would make them as tall as a house!) So Isaac has given his height in millimetres and his height in metres is 1098 ÷ 1000 = 1.098 m. Jasmine has given her height in centimetres, so her height in metres is 112 ÷ 100 = 1.12 m. Kim’s height is in metres already, so Kim is 1.1 m tall. So, the heights in metres are:
| Isaac | 1.098 |
| Jasmine | 1.120 |
| Kim | 1.100 |
(Inserting a 0 to the right of Jasmine’s 1.12, and two 0s to the right of Kim’s 1.1, has no effect on the value but is useful for comparisons as here.)
Comparing from the left, all have 1s in the units column. Isaac has a 0 in the tenths column, but Jasmine and Kim have 1s in the tenths column. So Jasmine and Kim are both taller than Isaac. In the hundredths column, Jasmine has 2 and Kim has 0. So Jasmine is the tallest.
Try some yourself
Activity 20
Place the following masses in order, with the lightest first:
2125 mg 1.9 g 0.02 kg
Answer
To compare these masses, convert them all to the same units (it doesn’t matter which unit you choose, so long as all are converted to the same). Choosing grams gives 2.125 g, 1.9 g and 20 g. Placing these in order gives:
1.9 g, 2.125 g, 20 g.
In the original units, this is
1.9 g, 2125 mg, 0.02 kg.
Activity 21
Place each of the following sets of quantities in order, smallest first.
(a) X = 0.5 l Y = 490 cl Z = 510 ml
(b) X = 20p Y = £0.02
(c) X = 0.039 kg Y = 4 g Z = 30 000 mg
Answer
(a) First convert to centilitres, say:
X is 50 cl; Y is 490 cl; Z is 51 cl.
So the order is X, Z, Y.
(b) First convert to pence, say:
X is 20p; Y is 2p.
So the order is Y, X.
(c) First convert to grams, say:
X is 39 g; Y is 4 g; Z is 30 g.
So the order is Y, Z, X.
3 Arithmetic
Although you may have a calculator at your disposal, you need to be able to carry out some calculations (usually with simpler numbers) in order to check your calculator work. Actually handling numbers, on paper or in your head, helps you to understand the nature of the calculations you perform on your calculator and gives you a deeper understanding of the underlying mathematical processes. In some cases, it really is quicker and easier to carry out a calculation by hand rather than key it into your calculator. However, do use your calculator for more cumbersome arithmetic.

The arithmetic system works not only for positive whole numbers but also for fractions, decimals and negative numbers. It can also be used when letters represent unknown numbers (algebra). It is therefore important to understand the principles for whole numbers, so you can extend these ideas to include different types of numbers.

3.1 Arithmetic with whole numbers
When you are adding or subtracting whole numbers, an important thing to keep in mind is the place value of the figures. It is often a good idea to set out the numbers in columns before doing the arithmetic.
Example 11
(a) There are 4985 people living in a village and 93 people living in a nearby hamlet. How many people live in the village and the hamlet in total?
(b) Of the total number of people in the village and hamlet, 1352 are under voting age. How many people are eligible to vote?
Answer
(a) There are 5078 people altogether.
An alternative method is to note that 93 is 7 less than 100. So add 100 to 4985 (5085) and subtract 7 (5078).
(b) 3726 people are eligible to vote.
Try some yourself
Activity 22
Carry out the following calculations, without using a calculator.
(a) A million pound lottery prize minus a three hundred pound administrative charge.
(b) The sum of cheques for £25 and £1029, to pay into a bank account.
Answer
(a) £999 700 remains.
(b) The total is £1054.
3.2 Multiplying and dividing
To multiply and divide by 10, 100, 1000, etc., write the digits in their place value columns. To multiply, move the digits to the left (replacing the numbers on the right with zeros) and to divide move them to the right (putting in a decimal point, and any zeros necessary for the place value).
Multiplication and division by whole numbers in general can be carried out by combining this technique with a knowledge of the multiplication tables up to 10.
Example 12
A machine in a factory puts tops on bottles at the rate of 1 every second.
(a) How many bottles does it top in a 10 hour working day?
(b) How many bottles does it top in a 30 day month, at 10 hours a day?
Answer
(a) There are 60 seconds in a minute and so it puts on 60 tops a minute. There are 60 minutes in an hour so it puts on 60 × 60 tops in an hour, which gives 3600.
There are many ways to do this e.g. think of 60 × 60 as 6 × 10 × 6 × 10, which is 6 × 6 × 10 × 10, i.e. 36 × 100, giving 3600 as before.
However you tackle it, the important thing is to remember the place values of the numbers.
So it tops 3600 bottles an hour. In 10 hours it tops 3600 × 10 = 36 000 bottles.
It tops 36 000 bottles in a 10 hour day.
(b) To find out how many bottles it tops in 30 days, multiply 36 000 by 30.
This is 36 000 × 3 × 10 = 1 080 000.
So the factory machine tops 1 080 000 bottles a month (just over a million).
The factory puts on 1 080 000 bottle tops in 30 days.
Try some yourself
Activity 23
Candles are sold in boxes of 40. How many candles are there in 30 boxes?
Answer
One box has 40 candles.
10 boxes have 40 × 10 candles = 400 candles.
30 boxes have 40 × 3 × 10 candles or 40 × 10 × 3 or 400 × 3 or 1200 candles.
Activity 24
(a) A doctor prescribes 3 pills a day and the prescription is to last for 4 weeks. How many pills should the pharmacist supply?
(b) Apples are sold in a pack of 7 for 95 p or singly 14 p each. Which is the better buy?
Answer
(a) There are 7 days in a week, so 4 weeks is 7 × 4 = 28 days.
The number of pills required is 28 × 3 = 84.
(b) The apples in packs cost p each.
Dividing 95 by 7 gives ,
which is less than the 14p per apple sold singly.
Alternatively, you could compare the cost of 7 apples: 7 apples at 14p each would cost 98p, which is more than 95p. So the apples in the pack would appear to be the better buy. (However, if you do not want 7 apples, and are likely to leave some of them to rot, you would be better off just buying the number of apples you want!)
Activity 25
Describe, in your own words, the effect of multiplying any number by (a) 1, (b) 0.
Answer
(a) Multiplying by 1 gives an answer the same as the original number. (There are many possible ways of wording this. You may have said it ‘leaves the number unchanged’ or ‘has no effect’.)
(b) Multiplying by 0 always gives 0.
Activity 26
Place the following times in order, shortest first:
four weeks; 29 days; 360 hours.
Answer
Convert all the times to days, say:
four weeks is 4 × 7 = 28 days;
29 days is already in days.
To convert 360 hours to days, divide by 24.
Writing it as you may spot that you can divide top and bottom by 12 to give = 15.
(Or you can divide 360 by 12 and then by 2 to give the same result as dividing by 24.
Alternatively you may say 10 days is 240 hours, 5 days is 120 hours, so 15 days is 360 hours.)
So, in order:
360 hours, 4 weeks, 29 days.
3.3 Division
Division is probably the most awkward of the four arithmetic operations. Since you may have a calculator, you do not need to be able to carry out complicated divisions by hand, but you do need to carry out simple divisions in order to check your calculator calculations. Division is the reverse process of multiplication. The quantity 12 ÷ 3 tells us how many times 3 goes into 12. Since 4 × 3 = 12, 12 ÷ 3 = 4.
Example 13
Small candles are sold in boxes of 40. How many boxes do you need in order to have 1000 candles?
Answer
To solve the problem, you need to know how many times 40 goes into 1000.
There are several ways to do this. One is to divide 1000 by 40:
So its value is unchanged if top and bottom are multiplied or divided by the same number.
Here, notice that top and bottom are both divisible by 10.
So you need 25 boxes of candles.
Alternatively, you might say 1 box gives 40, so 10 boxes give 400, 20 boxes give 800, 5 boxes give 200, so 25 boxes give 1000.
Try some yourself
Activity 27
(a) Divide a £27 000 jackpot prize equally among 9 people in the syndicate.
(b) Divide a £27 000 jackpot prize equally among 900 people in the syndicate.
Answer
(a) 27 000 ÷ 9 = 3000.
They get £3000 each.
(b)
.
They get £30 each.
3.4 Order of calculations
You may have noticed that sometimes the order in which calculations are carried out seems to matter and sometimes it does not. When using a calculator, it is very important to know the order in which it will do calculations. It is not always the order in which you enter them.
Although written English is read from left to right, this is not the case for all written languages (Chinese is read top to bottom, right to left). With mathematics, the order of the written operations does not always indicate the order in which they should be carried out.
Example 14
(a) Multiply 3 by 365. How many days are there in 3 years?
(b) Divide 366 by 3 to find out how many days there are per term, in a 3-term leap year.
(c) Does it matter if you interchange the numbers in each of the sums you did above?
Answer
(a) Multiplying by 365 is quite hard work, whereas multiplying by 3 is comparatively easy. Since 3 lots of 365 are the same as 365 lots of 3, it makes no difference whether you multiply 3 by 365 or multiply 365 by 3.
3 × 365 = 365 × 3 = 1095.
Since 3 × 365 = 1095, there are 1095 days in 3 years, provided one is not a leap year. If it were there would be 1096.
(b) 366 ÷ 3 = 122. So there will be 122 days.
(c) 3 × 365 = 365 × 3
So you can interchange the numbers in (a).
But 366 ÷ 3 does not give the same answer as 3 ÷ 366.
So you cannot interchange the numbers in (b).
To see that dividing 3 by 366 is not the same as dividing 366 by 3 note the following:
gives a value of over a hundred, whereas is much less than 1.
When you multiply two numbers together, it makes no difference which number you write first.
When you divide one number by another, it does matter which number you write first.
If you add two numbers, the order does not matter,
3 + 2 = 2 + 3,
but the same is not true with subtraction,
3 − 2 ≠ 2 − 3.
(≠ means ‘is not equal to’.)
When adding two numbers together, it makes no difference which number you write first.
When subtracting one number from another, it does matter which number you write first.
Try some yourself
Activity 28
Look at the rules in the boxes above.
Write in your own words the rules for multiplying and dividing, adding and subtracting two numbers, giving an example of each.
Answer
When adding two numbers together, or multiplying two numbers together, it makes no difference which number you write first. You get the same answer either way round.
e.g. 3 + 4 = 4 + 3, and 3 × 4 = 4 × 3.
When subtracting one number from another or dividing one number by another, it does matter which number you write first. You get different answers the other way round.
e.g. 8 − 4 = 4 is not the same as 4 − 8 = −4; and 8 ÷ 4 = 2 is not the same as 4 ÷ 8 = 1/2.
Activity 29
Is the following statement true or false?
When adding three numbers together, it doesn’t matter in which order you add them.
Answer
True. For example 2 + 3 + 4 is the same as 4 + 2 + 3.
3.5 Several calculations and using brackets
Sometimes you may want to make several calculations in succession, and the order in which the calculations are performed may or may not be significant. For example, if you want to add 12 + 7 + 13, it makes no difference which of these two processes you adopt:
add the 12 and 7 first, to give 19, and then the 13, to give 32;
or
add the 7 and 13 first, to give 20, and then add this to 12 to give 32 again.
Brackets can be used in a calculation to mean ‘do this first’.
Although (7 + 13) + 12 is the same as 7 + (13 + 12), sometimes the order of calculation does make a difference:
(7 − 12) + 13 is not the same as 7 − (12 + 13).
Example 15
Calculate (7 + 3) × 2 and 7 + (3 × 2).
Answer
To find (7 + 3) × 2, first do the calculation in brackets to get 7 + 3 = 10.
Then multiply by 2 to get 10 × 2 = 20.
For the second calculation, to find 7 + (3 × 2), first calculate 3 × 2 to give 6.
Then add to 7 to give 13. So (7 + 3) × 2 ≠ 7 + (3 × 2).
Try some yourself
Activity 30
Carry out the following calculations, without your calculator.
(a) 3 × (60 + 70).
(b) (3 × 60) + 70.
(c) (70 − 60) ÷ 5.
Check your answers using your calculator.
Answer
(a) 3 × (60 + 70) = 3 × 130 = 390.
(b) (3 × 60) + 70 = 180 + 70 = 250.
(c) (70 − 60) ÷ 5 = 10 ÷ 5 = 2.
With or without brackets
Brackets are not always given in a calculation, and there are rules which tell you in which order to do the calculations in the absence of brackets. The following is the order that scientific calculators normally use.
Calculations are performed in the following order:
Brackets;
Powers (e.g. squaring or cubing a number);
Division and Multiplication (performed in the order written, left to right);
Addition and Subtraction (performed in the order written, left to right).
If you have a calculator handy, check that it follows these rules.
Example 16
Calculate 10 + 3 × 7.
Answer
Multiplication is done before addition (unless brackets tell you otherwise) so
10 + 3 × 7 = 10 + 21 = 31.
Sometimes brackets are implied in division. For example,
Try some yourself
Activity 31
Insert brackets in the following calculations to emphasise the order in which a scientific calculator would perform them, then do the calculations by hand and on your calculator, with and without the brackets, as a check.
(a) 3 × 60 + 70.
(b) 10 − 15 ÷ 5.
(c) 20 − 2 × 8.
(d) 3 + 16 − 10.
(e) 3 × 10 ÷ 5.
Answer
(a) 3 × 60 + 70 = (3 × 60) + 70 = 180 + 70 = 250.
(b) 10 − 15 ÷ 5 = 10 − (15 ÷ 5) = 10 − 3 = 7.
(c) 20 − 2 × 8 = 20 − (2 × 8) = 20 − 16 = 4.
(d) 3 + 16 − 10 = (3 + 16) − 10 = 19 − 10 = 9.
(e) 3 × 10 ÷ 5 = (3 × 10) ÷ 5 = 30 ÷ 5 = 6.
Activity 32
In which of the calculations in Activity 31 does the order of the calculations make a difference?
Answer
The order makes a difference in calculations (a), (b) and (c) of Activity 31.
Activity 33
(a) Calculate
(b) Does the calculation in part (a) represent an exception to the ‘division before addition’ rule?
Answer
(a)
= 24 ÷ 8 = 3
(b) No, because there are implicit brackets around each of the top and bottom line of the fraction. When you write one number over another, you should treat the expressions above and below the line as if they were each in brackets. So the fact that the additions in part (a) were carried out before the division does not represent an exception to the ‘division before addition’ rule; it simply follows the ‘brackets before division’ rule.
Activity 34
The target score in a game of darts is obtained by subtracting the score of the three darts thrown in a player’s turn from the current target score on the board. In the game of ‘301’, the target score starts at 301. If a player’s first three darts are a double 19, a single 20 and a treble 17, what is the new target score?
Answer
The player scores 2 × 19, 20 and 3 × 17, which gives 38 + 20 + 51 = 109.
301 − 109 gives a new target score of 192.
Activity 35
Are the following statements true or false?
(a) When carrying out an addition and a multiplication, such as 2 + 3 × 4, it doesn’t matter whether you do the addition or the multiplication first.
(b) Putting brackets into an expression can change the order of the calculations.
Answer
(a) False. Carrying out the addition first gives 2 + 3 = 5, then multiplying by 4 gives 20. Carrying out the multiplication first gives 3 × 4 = 12, then adding to 2 gives 14 (which is the correct procedure here).
(b) True. For example writing brackets around 2 + 3 in the expression 2 + 3 × 4 gives (2 + 3) × 4 = 20, whereas without the brackets you should carry out the multiplication first to give 14.
3.6 Arithmetic with decimals
Arithmetic with decimals is much the same as arithmetic with whole numbers, but continue to take care with place value.
Addition and subtraction with decimals
Addition and subtraction can be carried out with decimals just as for whole numbers. Take care to write the numbers in their correct columns and keep the decimal points in line under each other.
Example 17
(a) Add 303.035 kg and 7.77 kg.
(b) Subtract 7.77 kg from 303.035 kg.
Answer
Remember to supply a ‘0’ at the end of 7.77 to keep the number of decimal places the same.
(a) The answer is 310.805 kg.
(b) The answer is 295.265 kg.
(With an awkward subtraction like this, a useful check is to add 7.77 to 295.265 to make sure that you get back to 303.035.)
Try some yourself
Activity 36
Without using your calculator, find the following:
(a) 100.001 + 10.1
(b) 100.001 − 10.1
Answer
(a)
(b)
Activity 37
Suppose you went shopping with a friend and your combined bill came to £85. You knew that you had spent £47.65. What was your friend’s share of the bill?
Answer
Your friend’s share of the bill is £85 − £47.65 = £37.35. There are many ways to do this subtraction. Setting out as a formal sum is one approach, but counting on (as an assistant may do to give change) is another (from £47.65 a further 35 p is needed to make £48, then £2 to make £50 and £35 to make £85 gives £37.35).
3.7 Multiplying and dividing with decimals
Multiplication and division of decimal numbers are carried out just as with whole numbers, except that now you can carry out the division even when one number does not divide exactly into the other. You also need to take care about the position of the decimal point. So check your answer is sensible.
Example 18
(a) If somebody’s hair grows at the rate of 0.4 cm a week, how much will it grow in 52 weeks or one year?
(b) How long would it take to grow their hair 10 cm?
(c) How long would it take to grow their hair 3 cm?
Answer
(a) In 52 weeks it grows 52 × 0.4 cm.
To multiply by 0.4, multiply by 4 and shift the digits one place to the right,
52 × 4 = 208. So 52 × 0.4 = 20.8.
So the hair will grow 20.8 cm in a year.
(0.4 is just under a half and half of 52 is 26, so the answer is sensible.)
Notice that multiplying by 0.4 gives an answer smaller than 52.
(b) You need to know how many times 0.4 cm goes into 10 cm, so divide 10 by 0.4,
10÷ 0.4 = = (multiply top and bottom by 10).
Now carry out the division: 100 ÷ 4 = 25.
So it would take 25 weeks to grow 10 cm.
(Check: 10 cm is about half of the previous answer of 20.8 cm which took a year, so will take about half a year. 25 weeks is near enough half a year, so the answer is sensible.)
(c) There are several ways of doing this. You might do it formally as
Carrying out the division gives 7.5.
Alternatively you might do it more informally: it grows 4 cm in 10 weeks,
and 3 cm is three-quarters of 4 cm,
so the answer is three-quarters of 10 weeks,
i.e. × 10 = 7.5 weeks.
Therefore it would take 7.5 weeks to grow 3 cm.
(Check: 3 cm is a bit less than a third of 10 cm which takes 25 weeks, so will take a bit less than a third of 25 weeks. 7.5 weeks is near enough a third of 25 weeks, so the answer is sensible.)
Try some yourself
Activity 38
Evaluate each of the following:
(a) 7.9 × 0.8
(b) 82.3 × 40
(c) 7.20 ÷ 0.8
(d) 62.30 ÷ 40
Answer
(a) 7.9 × 0.8 = 6.32
(multiply by 8 then shift the digits one place to the right).
(b) 82.3 × 40 = 3292
(multiply by 4 then shift the digits one place to the left).
(c)
(d)
Activity 39
Use your answer to Activity 38 above to evaluate the following.
(a) Special cheese is £7.90 per kilo. How much does 0.8 kilos cost?
(b) Petrol is 82.3p per litre. How much does 40 litres cost?
(c) The till receipt showed the cheese cost £7.20, and you bought 0.8 kilos. How much was it per kilo?
(d) The bill was £62.30 for 40 small children’s party hats. How much were they each? Was there an error in the bill or a discount?
Answer
(a) 0.8 kilos of cheese costs 0.8 × £7.90 = £6.32.
(b) 40 litres of petrol costs 40 × 82.3p = 3292p = £32.92.
(c) The cheese costs £7.20 ÷ 0.8 = £9 per kilo.
(d) Each hat costs £62.30 ÷ 40 = £1.5575 each, but they must be a whole number of pence each so only two decimal places are meaningful. Hence there was either an error or some discount.
3.8 Order of decimal calculations
The same rules about the order of calculations apply to decimals as apply to whole numbers.
Calculations are performed in the following order:
Brackets;
Powers (e.g. squaring or cubing a number);
Division and Multiplication (performed in the order written, left to right);
Addition and Subtraction (performed in the order written, left to right).
Example 19
Calculate 3.5 + 0.7 × 8 ÷ (4.6 − 2.6).
Answer
Brackets first: 4.6 − 2.6 = 2.0, so calculate 3.5 + 0.7 × 8 ÷ 2.0.
Multiply next: 0.7 × 8 = 5.6, so calculate 3.5 + 5.6 ÷ 2.0.
Divide next: 5.6 ÷ 2 = 2.8, so calculate 3.5 + 2.8.
Lastly add: 3.5 + 2.8 = 6.3.
So the answer is 6.3.
Try some yourself
Activity 40
Without using your calculator, find the following.
(a) 75.6 ÷ 0.6
(b) 75.6 × 0.6
(c) 100.001 + 75.6 ÷ 0.6
(d) (100.001 + 10.1) × 60
Answer
(a)
(b) 75.6 × 0.6 = 75.6 × = 7.56 × 6 = 45.36.
(c) Carrying out the division first, use the result of part (a) to give:
100.001 + 75.6 ÷ 0.6 = 100.001 + 126
= 226.001.
(d) Carry out the addition in brackets first:
(100.001 + 10.1) × 60 = 110.101 × 60 = 1101.01 × 6 = 6606.06.
Activity 41
Try dividing 10 by 3, first without using your calculator, and giving your answer as a decimal. What is the difficulty? What answer does the calculator give?
Answer
10 ÷ 3 gives
and so on.
Each time you divide by 3 you get a remainder 1, which gives 10 in the next column, so the decimal carries on forever. This is called a recurring decimal, because the 3 recurs repeatedly.
A scientific calculator gives 3.333333333 (it rounds to 10 digits).
Activity 42
Is the following statement true or false?
Multiplying one number by a second number always gives an answer greater than the first number.
Answer
False. For example, multiplying 7.9 × 0.8 in Activity 38(a) gave 6.32, which is less than 7.9. In general multiplying a positive number by a number less than one gives a smaller number.
3.9 Addition and subtraction with fractions
Addition and subtraction with fractions can be quite awkward, particularly when fractions are mixed with whole numbers and when the fractions have different denominators. In such cases you may need to use your calculator. However try to gain confidence in handling simple fractions.
To add two fractions with the same denominator, just add the numerators. For example,
Just as 3 eggs plus 2 eggs is 5 eggs, so 3 eighths plus 2 eighths is 5 eighths.
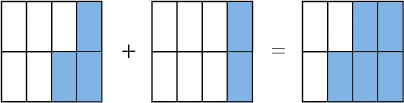
To subtract one fraction from another, where the denominators are the same, just subtract one numerator from the other. For example,
Just as 5 oranges minus 3 oranges is 2 oranges, so 5 twelfths minus 3 twelfths is 2 twelfths,
but is the same as . So the simplest answer is .

However, if the denominators are different, the calculation is a bit more awkward. The first thing to do is to rewrite the fractions as equivalent fractions where the denominators are the same.
A useful mathematical technique with things you can’t immediately handle is to put them in a form where you can handle them.
Example 20
Evaluate
Answer
You cannot add quarters and eighths directly. You need to change them into the same thing.
It is possible to change quarters to eighths.
is equivalent to : .
So make the denominators the same, i.e. both 8.
Try some yourself
Activity 43
Evaluate each of the following.
(a)
(b)
(c)
(d)
Answer
(a)
(b)
(c)
(d)
3.10 More difficult fraction sums
Sometimes you have to find equivalent factions for all fractions in the sum in order that the denominators are the same.
To add or subtract fractions, use equivalent fractions to make the denominators the same and then add or subtract the numerators.
Example 21
Evaluate .
Answer
You cannot change halves to thirds or vice versa, but you can change them both to sixths.
and . So .
Try some yourself
Activity 44
Is the following statement true or false?
Adding the same number to the top and bottom of a fraction gives you an equivalent fraction.
Answer
False. For example adding 2 to the top and bottom of gives . But is not equivalent to .
Activity 45
Explain in your own words how to add two fractions, as if to someone who does not know how to do it.
Answer
There are obviously many different ways of explaining this. For example one student said:
‘First look at the bottom number of each fraction. If these are the same, then this is also the bottom number of the answer. To get the top number in the answer, add the two top numbers in the given fractions.
‘If the bottom numbers are different, multiply the top and bottom of the first fraction by the bottom number of the second. Then multiply the top and bottom of the second fraction by the bottom number of the first. Now the two fractions have the same bottom number so they can be added as above.’
Your wording may have been very different but it should have given instructions for the case when the denominators are the same and when they are not. Note that the method described here will always work, when bottom numbers are different, although in some cases a quicker method is possible.
3.11 Multiplication of fractions
Multiplication by a whole number is really just repeated addition, 4 × 3 is 4 times 3:
In the same way,
Just add the numerators since the denominators are the same.
You may have noticed that the answer is the same as if you had multiplied the numerator of by 4:
Now look at an example where two fractions are multiplied.
Example 22
Isaac and Jasmine are helping themselves to some pizza. Isaac takes of the pizza and gives of this portion to Jasmine. How much pizza does Jasmine get?
Answer
She gets of , which just means .
Isaac’s portion is of the pizza. Divide the (i.e. ) into 4 portions and Jasmine gets 3 of them. Each piece is of the whole pizza, and three of these pieces constitute of the whole pizza. So the answer is that Jasmine gets three twelfths of the pizza. The calculation to which this corresponds is
Notice that , so an equivalent answer is that Jasmine gets a quarter of the pizza.
Notice that in the example above, when multiplying two fractions together you could just multiply the numerators and multiply the denominators, i.e.
This is true in general.
To give the answer in its simplest form, divide top and bottom by the common factor 3 to give
You can confirm from the diagram above that Jasmine’s share is a quarter of the whole pizza. There is a quicker way of getting to the answer in its simplest form, known as cancelling. Look again at the fraction
Divide top and bottom by 3, and show this by crossing off, or cancelling, the threes,
To multiply fractions, multiply the denominators together and the numerators together, cancelling any factors which the numerators and denominators have in common.
Try some yourself
Activity 46
Evaluate each of the following.
(a)
(b)
(c) of 2
(d) of
Answer
(a) (Cancel by 3 and 11)
(b) (Cancel by 5 and 3)
(c) of 2 means
(d) of means
Activity 47
A school contains 720 pupils. are girls. How many girls are there in the school?
Answer
You want of 720 or . So there are 270 girls in the school.
Alternatively of 720 is 90. So of 720 = 3 × 90 = 270.
Activity 48
If you divide a cake into 12 equal pieces and then eat 3 pieces, what fraction of the cake is left?
Answer
You have eaten (or ) of the cake. So there is (or ) of the cake left.
Activity 49
A recipe specifies a cooking time of hour and suggests checking and basting of the way through the cooking time. After how long should you check it?
Answer
Half an hour. There are several ways to do this calculation.
For example, one third of three quarters is one quarter (in symbols, ). Hence, two thirds (of three quarters) is two quarters, or a half: .
Alternatively gives , i.e. .
Another method is to cancel to give: .
You might also have converted hours to minutes:
now is 45 minutes, and of 45 minutes is 30 minutes.
So check it after half an hour.
3.12 Division by fractions
Before considering division of fractions, it is helpful to think about division of whole numbers.
6 ÷ 2 asks for the number of twos in 6: 6 ÷ 2 = 3, since three twos are six (3 × 2 = 6).
In a similar way, 6 ÷ is asking for the number of halves in 6. Suppose a friend is making salad decorations for plates of sandwiches. He has 6 tomatoes and wants to know how many half tomatoes this will give. This will be 6 ÷ . So think of the 6 as 6 whole tomatoes.
Each tomato contains two half-tomatoes, so 6 tomatoes contain 6 × 2 half-tomatoes. Hence
Thus dividing by is the same as multiplying by 2.
Similarly 2 ÷ is asking for the number of quarters in 2. Think of two cakes.
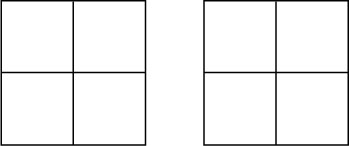
Each cake contains 4 quarters: the two cakes contain 8 quarters.
Expressed in figures this is
Hence dividing by is the same as multiplying by 4.
This illustrates the rule for dividing by fractions of the form .
To divide by , multiply by n (n can be any number except zero).
Try some yourself
Activity 50
Evaluate 3 ÷
Answer
3 ÷ = 3 × 3 = 9
There are 9 thirds in 3.
3.13 More division with fractions
How about other fractions? What is 6 ÷ ? This means how many are there in 6? Consider six squares, divided into quarters, and count how many groups of three quarters there are.
Activity 51
Answer

Three quarters is 3 × . So dividing by is the same as dividing by 3 and by . Dividing by is multiplying by 4. So dividing by is the same as dividing by 3 and multiplying by 4, which is multiplying by . So 6 ÷ = 6 × = = 8.
The general rule for dividing by a fraction can be stated as follows.
To divide by a fraction, turn the fraction upside down and multiply.
Does this also work for dividing by ? Yes, because multiplying by n is the same as multiplying by . It also works for division of whole numbers: dividing by 4 (= ) is the same as multiplying by .
Example 23
Evaluate:
Answer
Using the rule above,
This is
(divide top and bottom by 3).
Alternatively divide top and bottom by 3 by cancelling by 3 to give
So .
Turning a fraction upside down is called finding its reciprocal.
The reciprocal of is . The reciprocal of is , i.e. 6.
So an alternative formulation of the rule for dividing by a number can be stated as follows.
Division by a number is the same as multiplication by its reciprocal.
Try some yourself
Activity 52
Evaluate each of the following.
(a)
(b)
Answer
(a) and . So
(b) .
Activity 53
Evaluate each of the following, giving each answer in its simplest form.
(a)
(b)
Answer
(a) (reciprocal of is ).
(b) (reciprocal of is ).
Activity 54
Explain how to multiply fractions, to somebody who does not know how to do it.
Answer
There are several ways of explaining this. For example:
‘To multiply two fractions, multiply the top two numbers together (the numerators) and multiply the bottom two numbers together (the denominators). To give the answer in its simplest form, check whether top and bottom numbers have a factor in common and, if so, divide through by it.’
Or
‘To multiply two fractions by cancelling, find a number that goes into (divides) a number on the top and a number on the bottom i.e. cancel. Repeat this until there are no numbers left which will cancel with each other. Then multiply together the top two numbers (the numerators) and the bottom two numbers (the denominators). This fraction should be in its simplest form.’
3.14 Mixed numbers
In order to do arithmetic with mixed numbers like , it is often best to write them as a simple fraction, that is, one number over another.
Multiplication or division involving mixed numbers is done by converting them to fractions first.
Example 24
(a) Write as a simple fraction.
(b)
To enter on a calculator, you can input .
is called a ‘mixed number’.
Answer
(a)
2 is the same as
So
(b) is so
In multiplication or division involving mixed numbers like , convert the mixed number to a (top heavy) fraction.
Try some yourself
Activity 55
Evaluate the following, giving your answer in its simplest form.
Answer
. So .
3.15 Arithmetic with negative numbers
In order to understand arithmetic with negative numbers, it is helpful to see how arithmetic can be represented on the number line. The strategy is to start with simple examples of whole positive numbers and then generalise to negative numbers. The same principles must apply!
Addition on the number line
For example, to find 8 + 3 start at 8 and move 3 units to the right.

giving 8 + 3 = 11. Adding a positive number means moving to the right along the number line.
Another way of considering the arithmetic of positive and negative numbers is to consider them as the total value of the contents of a piggy bank, belonging to a child (Thomas). The numbers on the above number line can represent the value of Thomas’s piggy bank. Calculations represent transactions involving the piggy bank. When Thomas gets pocket money or gifts of money, he adds them into his piggy bank. If Thomas had £8 in his piggy bank and adds £3 (from his pocket money) the value of the piggy bank in pounds is 8 + 3 = 11.
When he spends money (on toys usually) he takes money out (subtracts). If there is not enough money in the piggy bank, he needs to borrow money. When he borrows money from his family, they note the debt on a piece of paper headed ‘IOU’ (I owe you). Thomas puts the ‘IOUs’ into his piggy bank. IOUs represent a negative amount of money (or debts).
Now suppose, at another time, Thomas’s piggy bank contains an IOU for £3 when Thomas receives a gift of £5 to add to his piggy bank. £3 of this pays off the IOU and he has £2 left in the piggy bank. The transaction is represented by the calculation of the new value (in pounds) of the piggy bank
−3 + 5 = 2.
How is this represented on the number line? Adding a positive number is moving to the right.

Moving 5 units to the right from −3 gets us to 2. So −3 + 5 = 2.
Subtraction on the number line
Now what about subtraction? You can think of subtraction as undoing addition: adding 3 to 8 gets you 11, and so subtracting 3 from the answer, 11, gets you back to 8. Therefore, in terms of the number line, subtracting 3 from 11 means starting at 11 and moving 3 units to the left.
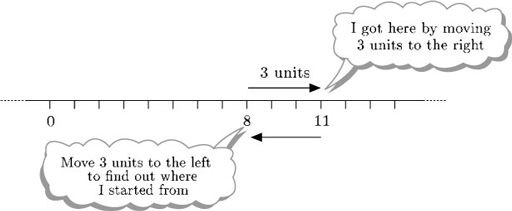
So 11 − 3 = 8. Subtracting a positive number means moving to the left along the number line. Thinking in terms of the contents of the piggy bank: if Thomas had £11 in his piggy bank and subtracts £3 (to buy a toy), he is left with £8.
Suppose on one occasion Thomas has £2 in his piggy bank. He wants to buy a toy for £5. 2 − 5 means starting at 2 and moving 5 units to the left.

This takes you back to −3, so 2 − 5 = −3.
So Thomas needs to borrow £3 and gets an IOU (from his mother) which he puts in his piggy bank. His piggy bank is worth −£3.
3.16 Addition of negative numbers
Now think about adding a negative number, by looking at the number line again. Suppose you start at 0. Since 0 + −3 is the same as −3, you would expect that adding −3 to 0 on the number line should take you to the point marked −3 on the number line. So, 0 + −3 = −3.
Suppose Thomas’s piggy bank were empty and he added an IOU for £3 to it. The value of the piggy bank would be −3.
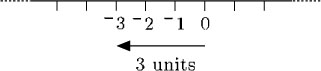
To reach −3 from 0, move 3 units to the left. In general to add a negative number you move to the left along the number line.
Adding a negative number is the same as subtracting the corresponding positive number.
In terms of Thomas’s piggy bank, a negative number is an IOU. Adding an IOU is the same as taking money out (subtracting a positive number).
Example 25
Evaluate each of the following:
(a) 11 + −3
(b) 2 + −5
Answer
(a) In piggy bank terms, this represents contents of £11 plus a £3 IOU. So the overall value is 11 + −3 = 11 − 3 = 8.

(b) Thomas’s piggy bank has £2 in it plus a £5 IOU. So it is worth 2 + −5 = 2 − 5 = −3.

Try some yourself
Activity 56
Evaluate each of the following and give an example from everyday life to illustrate the sum (e.g. Thomas’s piggy bank).
(a) −4 − 6
(b) 3 + −5
(c) −4 + −7
(d) −5 + 8
Answer
(a) −4 − 6 = −10.
If you have an overdraft of £4 and take out £6 you have an overdraft of £10.
(b) 3 + −5 = 3 − 5 = −2.
Thomas’s bank has £3 plus a £5 IOU, which is equivalent to a £2 IOU.
(c) −4 + −7 = −4 − 7 = −11.
A debit of £4 plus a debit of £7 is equivalent to a debit of £11.
(d) −5 + 8 = 3.
An overdraft of £5 plus a deposit of £8 results in a balance of £3.
3.17 Subtraction of negative numbers
Next consider subtraction of a negative number. In terms of Thomas’s piggy bank, subtracting a negative number is the same as taking away one of his IOUs. If his mother says ‘you have been a good boy today so I’ll take away that IOU for £3’ this is equivalent to him being given £3.
So, − (−3) = 3. Does this correspond with the number line interpretation of subtracting a negative number?
Consider the evaluation of 8 − −3. Continue to think of subtraction as undoing addition: adding −3 to 11 gives 8, and so subtracting−3 from the answer, 8, gets back to 11. So, in terms of the number line, subtracting −3 from 8 means starting at 8 and moving 3 units to the right.
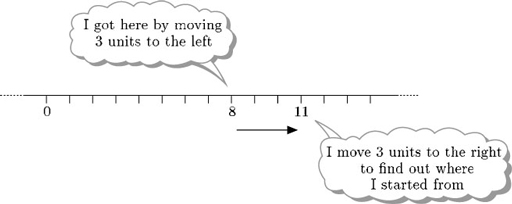
But moving 3 units to the right is the same as adding 3. So
8 − −3 = 8 + 3 = 11.
If on one occasion Thomas’s piggy bank is worth £8 in total (cash and IOUs) and his mother takes away a £3 IOU, the value of the piggy bank is 8 − −3 = 8 + 3 = 11.
Subtracting a negative number is the same as adding the corresponding positive number.
Try some yourself
Activity 57
Evaluate each of the following and give an example from everyday life to illustrate the sum (e.g. Thomas’s piggy bank).
(a) 4 − −2
(b) −3 − −5
Answer
(a) 4 − −2 = 4 + 2 = 6. .
A gift of £4 plus taking away a £2 debt is equivalent to a gift of £6.
(b) −3 − −5 = −3 + 5 = 2.
Acquiring a debt of £3 and taking away a debt of £5 results in being £2 better off.
3.18 Practical examples of negative numbers
Negative numbers occur in financial matters, in temperature or height measurements and many other practical situations.
Example 26
(a) If the value of a painting increases by £20 a year and it is worth £200 today, how much will it be worth in a year’s time? How much was it worth a year ago?
(b) Describe in words how to calculate the value of an object like a picture one year in the future or one year ago, given a constant annual increase.
(c) If the value of a washing machine decreases by £20 a year and it is worth £200 today, how much will it be worth in a year’s time? How much was it worth a year ago?
(d) If you regard a decrease as a negative increase, does your answer to (b) apply to the washing machine in (c)?
Answer
(a) The value of the painting in a year’s time is £200 + £20 = £220. The value of the painting a year ago was £200 − £20 = £180.
(b) To work out the value a year in the future, add the annual increase to the current value. To work out the value a year in the past, subtract the annual increase from its current value.
(c) The value of the washing machine in a year’s time is £200 − £20 = £180.
The value of the washing machine a year ago was £200 + £20 = £220.
(d) Yes. Thinking about the annual decrease as a negative increase, apply the rules in part (b) to carry out the calculation. The value of the washing machine in a year’s time is current value + annual increase, i.e. £200 + −£20 = £180.
The value of the washing machine a year ago is current value − annual increase, i.e. £200 − −£20 = 200 + 20 = £220.
So adding a negative increase is the same as subtracting the decrease.
Subtracting a negative increase is the same as adding the decrease.
Try some yourself
Activity 58
Answer the following questions:
(a) If you had £3 in your bank account and drew out £10, how much would you have left?
(b) The temperature was −5 °C on Monday and dropped overnight by 6 °C. What was the temperature on Tuesday morning?
Answer
(a) 3 − 10 = −7,
so you would have −£7 left, i.e. you would have a £7 overdraft.
(b) −5 − 6 = −11,
so the temperature was −11 °C.
Activity 59
Evaluate each of the following:
(a) −3 + −12
(b) −4 − −11
Think of a financial context where each might be an appropriate calculation (bear in mind that negative numbers can represent debts).
Answer
(a) −3 + −12 = −15 (a debt of £3 plus a debt of £12 gives a debt of £15).
(b) −4 − −11 = −4 + 11 = 7 (incurring a debt of £4 and being let off a debt of £11 results in being £7 better off).
Activity 60
Kim was walking in Israel. She started at 37 metres below sea level and ended up at 42 metres above sea level. How far had she climbed up?
Answer
Kim started at −37 m and ended at 42 m. You want 42 − −37 = 42 + 37 = 79. So Kim climbed 79 m.
3.19 Multiplication with negative numbers
Now that you have rules for addition and subtraction of negative numbers, think about multiplication and division.
Example 27
Describe each of the following in terms of the number line and the value of Thomas’s piggy bank:
(a) the multiplication of 3 times 5 (that is, 3 × 5);
(b) the multiplication of 3 times −5 (that is, 3 × −5).
Answer
(a) Three times 5 means adding three lots of 5, or do the move ‘5 units to the right’ three times.
Thomas’s piggy bank has three £5 notes in it. The value of the piggy bank in pounds is 3 × 5 = 15.
(b) 3 times −5 means adding three lots of −5, or do 3 times ‘move 5 units to the left’.
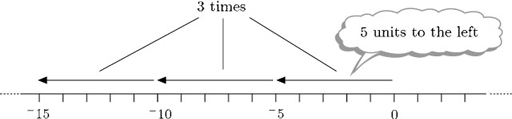
Thomas’s piggy bank has 3 IOUs each for £5 in it. The value of the piggy bank in pounds is 3 × −5 = −15.
So multiplying a negative number by a positive number gives a negative answer. But what does it mean to multiply by a negative number – how can you add something a negative number of times?
Think of multiplication by a positive number as repeated addition, and of multiplication by a negative number as repeated subtraction. If Thomas’ mother says she’ll take away three of his £5 IOUs, it is equivalent to giving him three £5 notes. So −3 × −5 = 3 × 5 = 15. He is £15 better off.
Example 28
Evaluate each of the following in terms of the number line and the value of Thomas’s piggy bank.
(a) 5 × −3
(b) −5 × −3
Answer
(a) Think of 5 times −3 as meaning ‘5 lots of −3’. So 5 × −3 means: do 5 times ‘move 3 units to the left’.
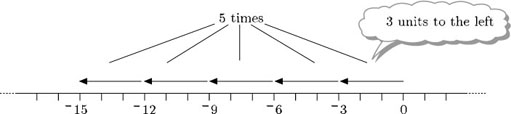
So 5 × −3 = −15.
In terms of the piggy bank Thomas has five £3 IOUs in it. The value in pounds is 5 × −3 = −15, which is equivalent to one £15 IOU.
(b) Thinking in terms of repeated subtraction, do 5 times ‘subtract −3’. Subtracting −3 means adding 3, or moving 3 units to the right. So do 5 times ‘move 3 units to the right’.
Subtracting −3 is the same as adding 3.
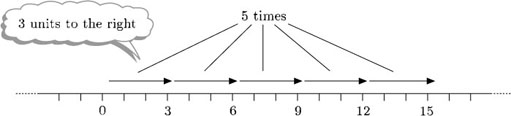
So −5 × −3 = 5 × 3 = 15.
Thomas’s mother takes away five £3 IOUs. This is equivalent to giving him £15.
The calculation in pounds is −5 × −3 = 5 × 3 = 15.
3.20 Multiplication rules
The rules for multiplying positive and negative numbers can be illustrated by the table below.
Multiplying a positive number by a positive number gives a positive answer.
Multiplying a negative number by a positive number gives a negative answer.
Multiplying a positive number by a negative number gives a negative answer.
Multiplying a negative number by a negative number gives a positive answer.
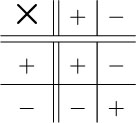
The painting and the washing machine from Example 26 can be used again, to illustrate these rules.
Example 29
A painting increases in value at £20 a year and a washing machine decreases in value at £20 a year. Each is worth £200 today.
(a) How much will each be worth in four years’ time?
(b) How much was each worth four years ago?
Answer
(a) To find the value in four years’ time, in each case add the annual increase (which is negative in the case of the washing machine) four times. So the value of the painting will be
£200 + 4 × £20 = £200 + £80 = £280
and the value of the washing machine will be
£200 + 4 × −£20 = £200 − £80 = £120.
(b) To find the value four years ago, subtract the annual increase from today’s value four times. So the value of the painting four years ago was
£200 − 4 × £20 = £120
and the value of the washing machine four years ago was
£200 − 4 × −£20.
But this is a matter of repeatedly subtracting a negative number, which is the same as repeatedly adding the corresponding positive number. So
£200 − 4 × −£20 = £200 + 4 × £20 = £280.
Try some yourself
Activity 61
Evaluate each of the following and where possible give an example from everyday life to illustrate the calculation.
(a) 4 × −3
(b) −2 × −7
(c) −3 × 5
Answer
(a) 4 × −3 = −12.
Four debts of £3 is a debt of £12.
(b) −2 × −7 = 14.
Thomas’s mother taking away two £7 IOUs is equivalent to giving him £14.
(c) −3 × 5 = −15.
Thomas gives away 3 five pound notes, which is equivalent to giving away £15.
3.21 Division rules
Lastly consider division. Dividing 8 by 2 means ‘How many times does 2 go into 8?’ or ‘What must you multiply 2 by to get 8?’. The answer is 4.
So to find 8 ÷ −2, you need to ask ‘What do I have to multiply −2 by to get 8?’. The answer is −4, since −2 × −4 = 8.
So 8 ÷ −2 = −4.
Similarly, to find −8 ÷ −2 you need to ask ‘what do I have to multiply −2 by to get −8?’ and the answer is 4, since −2 × 4 = −8.
So −8 ÷ −2 = 4.
Using this sort of argument you can work out the rules for division of and by negative numbers. They are remarkably similar to those for multiplication (as you might expect, since they are inverse processes).
Multiplying or dividing a positive number by a positive number gives a positive answer.
Multiplying or dividing a negative number by a positive number gives a negative answer.
Multiplying or dividing a positive number by a negative number gives a negative answer.
Multiplying or dividing a negative number by a negative number gives a positive answer.
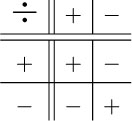
The last one is the most difficult to remember. If you are in doubt, you can always use your calculator to check.
These rules may be summarised as follows.
Multiplying or dividing two numbers of the same sign gives a positive answer.
Multiplying or dividing two numbers of different signs gives a negative answer.
Try some yourself
Activity 62
Give examples of all the rules for the division of and by positive and negative numbers.
Answer
Your list should look something like this.
Dividing a positive number by a positive number gives a positive answer.
4 ÷ 2 = 2.
Dividing a negative number by a positive number gives a negative answer.
−4 ÷ 2 = −2.
Dividing a positive number by a negative number gives a negative answer.
4 ÷ −2 = −2.
Dividing a negative number by a negative number gives a positive answer.
−4 ÷ −2 = 2.
Activity 63
Evaluate each of the following and where possible give an example from everyday life to illustrate the calculation.
(a) 24 ÷ −4
(b) −40 ÷ −4
(c) −45 ÷ 15
Answer
(a) 24 ÷ −4 = −6
Thomas has lots of £4 IOUs. A gift of £24 will subtract 6 of them.
(b) −40 ÷ −4 = 10
An IOU of £40 divided into smaller IOUs of £4 each (which could be paid off more easily from Thomas’s pocket money) gives 10 smaller IOUs.
(c) −45 ÷ 15 = −3
A debt of £45 shared between 15 people means each owes £3.
Activity 64
Evaluate each of the following.
(a) 7 × −6
(b) −56 ÷ −7
Think of a financial context where each might be an appropriate calculation (bear in mind that negative numbers can represent debts).
Answer
(a) 7 × −6 = −42
(7 debts of £6 result in a debt of £42).
(b) −56 ÷ −7 = 8
(a £56 debt divided into £7 debts gives eight £7 debts).
If you have a calculator check that it gives the same answers as yours.
4 OpenMark quiz
You might like to make some notes on the course for your own use later.
Now check your own learning by attempting the interactive quiz. You will get some helpful feedback after each attempt.
Conclusion
This free course provided an introduction to studying Mathematics. It took you through a series of exercises designed to develop your approach to study and learning at a distance and helped to improve your confidence as an independent learner.
Get careers guidance
The National Careers Service can help you decide your next steps with your new skills.
Acknowledgements
Except for third party materials and otherwise stated in the acknowledgements section, this content is made available under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Licence.
Course image: russellstreet in Flickr made available under Creative Commons Attribution-ShareAlike 2.0 Licence.
All written material contained within this course originated at The Open University.
Every effort has been made to contact copyright owners. If any have been inadvertently overlooked, the publishers will be pleased to make the necessary arrangements at the first opportunity.
Don’t miss out:
If reading this text has inspired you to learn more, you may be interested in joining the millions of people who discover our free learning resources and qualifications by visiting The Open University - www.open.edu/ openlearn/ free-courses
