Data and processes in computing
Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Friday, 19 April 2024, 8:24 PM
Data and processes in computing
Introduction
This course provides an introduction to data and processes in software, and provides a basis that enables these fundamental ideas to be developed in a clear and precise way. It has two main aims. The first is to illustrate how we can describe ways in which data may be structured and processed. The second is to introduce you to some vocabulary and concepts that help us to do this. The material is accessible to anyone with a little experience of the use of symbols in presenting ideas.
Section 1 provides a brief introduction to the course. It contains some new language that will be explained more fully in later sections. Read this section without spending too much time on it. The most important material in this course is that in Sections 2 and 4. Section 3 includes some ideas that are relatively difficult. You should read this section, but do not spend a great deal of time on it. Section 5 is of a similar length to Sections 2 and 4.
Overall, do not allow yourself to spend too long on any section while you are studying this course. You can always come back and reread material here if you find later that you need a more thorough understanding of some point.
This OpenLearn course provides a sample of Level 2 study in Computing & IT
Learning outcomes
After studying this course, you should be able to:
understand ways in which data may be stored and processed
distinguish between different forms of data, and use notations introduced in the course to show different forms of data
appreciate that fine details may be important when interpreting formal notation (for example, different types of brackets may be used to distinguish between different forms of data)
interpret a given function description
recognise correct syntax in formal expressions.
Key ideas
In this course, we will take an introductory look at two key ideas: forms of data handled by a software system, and the processes that may be applied to that data. These ideas are illustrated by a particular application — a supermarket till — but they are of general relevance in designing software systems. Important terminology will be highlighted in bold.
In this course we will look at some commonly occurring forms of data. We start with fundamental forms, such as numbers and characters (which are symbols that may be typed at a keyboard). We then go on to look at more complicated data structures.
A second crucial feature of data is the processes available to handle it. The processes needed in any particular application are a particular focus in software design. Here, we shall look at how in principle we can describe a process that manipulates data. This initial description will not be concerned with how the process is executed, but only with its effect.
This course will introduce two important mathematical ideas that help in offering clear and precise descriptions of software components relating to data and processes. These ideas are set and function.
Section 1 gives a brief introduction to how data and processes may arise in an application situation. Section 2 is concerned with fundamental forms of data, and the mathematical idea of a set. Section 3 looks briefly at some more structured forms of data. In Section 4 we look at processes, and the mathematical idea of function. Section 5 is concerned with processes of a particular sort. Examples of these processes are the addition of numbers (as in 5 + 6) and a comparison of two numbers (as in 3
1 At the supermarket
1.1 Number sequences
Imagine that you are at a modern supermarket and the cashier is processing the items from your basket or trolley. The electronic till (which is a form of computer) records each item that you have bought. Most items are scanned using a device that can read the barcode printed on the item.

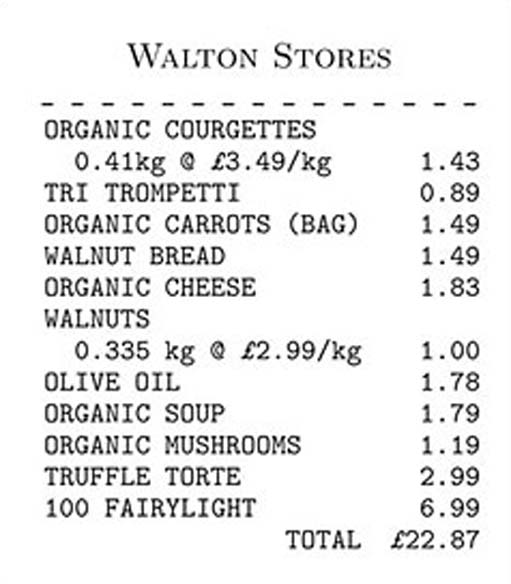
Items that need to be weighed (such as loose fruit and vegetables) do not have a barcode printed on them. Instead, the cashier looks up a different sort of code for these items and enters this manually at the till, together with the weight of the item purchased. If an error is made, the cashier may cancel the item just entered and try again. When all the items you have purchased have been processed, your final bill is calculated and you receive an itemised receipt (Figure 2).
Let us look a little more formally at some of the data that the supermarket computer system must store and use. As we do this, you will begin to get a flavour of the rigour that underpins the design of modern software. You will meet new vocabulary and concepts, try to get a general sense of what each new term means.
Each type of item stocked by the supermarket needs to be identified. As we have seen, this is done either using barcodes or, for weighed items, item codes of a different sort. Associated with each code is a variety of other item-related information. Perhaps the most obvious information is the price, and the description that appears on the receipt. (In the case of weighed items, the price is a unit price, giving the price per kilogram, for instance.) Other information associated with any item code might include the current stock level (so that new stock can be ordered as items are near to being out of stock), the name and address of the supplier, discount rates for multiple purchases, etc
Barcodes such as 5000119004048 can be interpreted as whole numbers. Whole numbers are called integers. Integers may be positive, negative or zero. (The codes for weighed items are also usually whole numbers.)
Prices and weights are not ordinarily presented as whole numbers. In Figure 2, the item price of walnut bread is shown as £1.49; the unit price of organic courgettes is £3.49 per kg and the weight of organic courgettes purchased is 0.41 kg (kg is the standard abbreviation for kilogram).
A number with a fractional part such as 1.49 is an example of a real number. The real numbers include numbers such as 3.497825 (and numbers such as √2, which cannot be expressed exactly as any fraction or decimal). Computers cannot represent such real numbers exactly. When dealing with a real number, we can only rely on a computer storing and manipulating an approximation of the number. Even though the extent of the approximation may seem small, this can present problems to the unwary software developer. To avoid problems here, we will represent prices as a whole number of pence, and weights as a whole number of grams. So, for example, the bill in Figure 2 includes a purchase of 335 grams of walnuts at 299 pence per kg.
As the items in a basket or trolley are scanned one after another, the till stores a sequence of codes. We use a precise notation to indicate a sequence. Suppose that the item codes scanned so far are 50773, 50412, 50330, 33777, 50773. If the codes were scanned in this order, then the till would store the sequence [50773, 50412, 50330, 33777, 50773]. If the same codes were scanned in a different order, then the till might store the sequence [50773, 50773, 50412, 50330, 33777]. Barcodes normally contain more digits. In our illustrative examples, we shall use shorter codes that are easier to read.
A sequence is a collection of items in a particular order. We shall write the items in a sequence between square brackets [ and ], and commas are used to separate the items in it (in other texts, you may see angled brackets 〈 and 〉 used to show a sequence, rather than [ and ]). These items are called the elements of the sequence. The order in which items appear in a sequence is important, so that [50773, 50412, 50330, 33777, 50773] is not the same as the sequence [50773, 50773, 50412, 50330, 33777]. Of course, the order in which the cashier checks your purchases does not matter in terms of the final cost. But, while the items are being entered, the order will often matter. For example, if an error occurs in scanning or weighing, the last item entered can usually be corrected using a ‘Cancel Last Item’ key on the till. Also, the itemised bill that you receive usually gives the items in the order in which they have been processed.
Item descriptions in Figure 2 include “ORGANIC SOUP” and “OLIVE OIL”. These descriptions are formed from characters that can be typed from a computer keyboard (possibly with the Shift key pressed). There are various points to note about characters. For example, upper- and lower-case versions of the same letter, such as ‘P’ and ‘p’, are different characters. A digit such as ‘5’ can be entered from the keyboard as a character, and it is vital to be clear that, in terms of its storage in computer memory, this is not the same thing as the number 5. This means that “SOUP”, for example, also forms a sequence. It is a sequence of characters, and could be written as [‘S’, ‘O’, ‘U’, ‘P’]. However, to do this would be tedious, since we will use sequences of characters frequently. So we often use the notation “SOUP”, just to make life easier! When we do this, we usually refer to the sequence of characters as a string.
Note that we have introduced a number of notational conventions. An individual character is written between single inverted commas, as in ‘P’ or ‘q’. Double inverted commas are used to show a sequence of characters such as “ORGANIC”. If we write out in full the string “ORGANIC COURGETTES 0.41kg @ £3.49/kg”, it is necessary to deal with the spaces between words. This use of double inverted commas only applies to sequences of characters. All other sequences are written using the square bracket notation introduced above. Spaces are characters like any others; they are obtained by pressing the space-bar on the keyboard. It is often desirable to indicate the space character explicitly by adopting a special symbol. We shall use ‘![]() ’. Thus, we may write [‘O’, ‘R’, ‘G’, ‘A’, ‘N’, ‘I’, ‘C’, ‘
’. Thus, we may write [‘O’, ‘R’, ‘G’, ‘A’, ‘N’, ‘I’, ‘C’, ‘![]() ’, ‘C’, ‘O’, ‘U’, ‘R’, ‘G’, ‘E’, ‘T’, ‘T’, ‘E’, ‘S’, ‘
’, ‘C’, ‘O’, ‘U’, ‘R’, ‘G’, ‘E’, ‘T’, ‘T’, ‘E’, ‘S’, ‘![]() ’, ‘0’, ‘.’, ‘4’, ‘1’, ‘k’, ‘g’, ‘
’, ‘0’, ‘.’, ‘4’, ‘1’, ‘k’, ‘g’, ‘![]() ’, ‘@’, ‘
’, ‘@’, ‘![]() ’,‘£’, ‘3’, ‘.’, ‘4’ ‘9’, ‘/’, ‘k’, ‘g’].
’,‘£’, ‘3’, ‘.’, ‘4’ ‘9’, ‘/’, ‘k’, ‘g’].
Imagine you are at the fifth till in the supermarket, and the data that constitutes your transaction is recorded by the supermarket's computer using the identifier till5. This is the name of an area in the computer's memory devoted to storing your transaction details. The data stored in till5 changes each time an item is scanned or entered, and so we refer to till5 as a variable. We call the data stored in the variable till5 at any moment in time the state of till5. Each time that the data stored by till5 changes, we say that the state of till5 has changed. You do not need to know anything about how the computer's electronic memory actually works.
These comments are not peculiar to the fifth till at the supermarket. The supermarket's computer stores data for each active till. The data for each till can be seen as a variable, and so needs its own identifier — such as till1, till2, and so on. Indeed, the term variable is used for any named area of computer memory, storing data that may change.
Now suppose that the variable till5 stores a sequence of barcodes. When the cashier starts a new transaction, no items have been entered, so the state of the variable till5 needs to start as a sequence with no elements, which we call an empty sequence and write as [ ]. If an item with code 50297 is then entered, then the state of till5 will change to [50297]. If an item with code 50152 is scanned next, then the state becomes [50297, 50152], and so on.
When a new item is recorded, the state of till5 changes, and changes in a way that is predictable. Specifically, the current state is changed by appending the newest item to the end of the sequence, giving a new state.
We have described the change of a till state in a way that is quite general. The description is not peculiar to the fifth till in the supermarket: it applies equally well to a transaction in progress at any till. Indeed, it describes a process that adds a new item to any variable storing data as a sequence.
| Item code | Item price (pence) |
|---|---|
| 33050 | 299 |
| 53151 | 440 |
| 77502 | 89 |
Now suppose the computer stores the prices of certain items as given in Table 1. To calculate the bill corresponding to purchases read by the cashier as [77502, 53151, 33050, 77502], we need to store the price associated with each item purchased. Let us assume that a second sequence is also being generated as each item is recorded, giving the price of the item. Suppose that this is stored as a variable price5. If the sequence of item codes were [77502, 53151, 33050, 77502], then the sequence of prices would be [89, 440, 299, 89]. Given this sequence, the total bill is obtained by simply finding the total of all the values in the sequence price5:
89 + 440 + 299 + 89 = 917 pence.
For simplicity, assume that there are no weighed items and no special offers.
This calculation does not change the state of the variable price5, but the value calculated certainly does depend upon the state of that variable.
Appending a new item at the end of a sequence, or adding a sequence of numbers, are both examples of the sort of processes that software needs to carry out time and time again. Recognising generality, and forms of data and processes on data that can be reused, are key skills in learning to design large and complex software systems.
Activity 1
Consider a process that changes the state of a variable storing a sequence by removing the last item from the sequence. So, for example, if the state of the variable was [22, 31, 53, 22, 13], then applying the process would change the state to [22, 31, 53, 22]. Suppose that this process is applied four more times. Write out the state of the variable after each application.
Discussion
The state starts as [22, 31, 53, 22]. After one more application of this process the state is [22, 31, 53]. If the process is applied again, the state becomes [22, 31]. If the process is applied again, the state becomes [22]. If the process is applied one more time, then the last item in the sequence is removed. We are left with a sequence containing no items, the empty sequence, which we write as [ ].
Since we use double inverted commas for strings, i.e. sequences of characters, we will use “ ” to denote the empty string in this course. In many computing texts, the symbol ξ is used.
Activity 2
How many characters are there in the string “I am it.”? Using the notational conventions introduced above for writing sequences and characters (including the space character), write this string out in full as a sequence of characters.
Discussion
This string includes eight characters in all, including two space characters and a full stop. Written in full, it is the following sequence of characters:
[‘I’,‘![]() ’,‘a’,‘m’,‘
’,‘a’,‘m’,‘ ![]() ’,‘i’,‘t’,‘.’].
’,‘i’,‘t’,‘.’].
Objectives for Section 1
After studying this section you should be able to do the following.
Recognise the terminology: character; string; integer; sequence; element (of a sequence); variable; identifier (of a variable); state (of a variable).
Use and interpret the notational conventions:
single inverted commas to show a character;
double inverted commas to show a string (sequence of characters);
‘
 ’ to make explicit a space character;
’ to make explicit a space character;the brackets [ and ] to delimit a sequence.
Exercises on Section 1
Exercise 1
(a) How many characters are there in the string “This text.”?
(b) Which of the following are integers: 3, 0, 98, 4, –22,
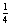 , ‘7’, [56]?
, ‘7’, [56]?(c) How many integers are there in the sequence [11, 23, 4, 56, 32]?
Answer
Solution
(a) There are ten characters: four in each word, a space, and a full stop.
(b) Each of 3, 0, 98, 4 and −22 is an integer.
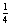 is not an integer because it is not a whole number. ‘7’ is a character, and is not an integer. [56] is a sequence containing one integer, but is not an integer.
is not an integer because it is not a whole number. ‘7’ is a character, and is not an integer. [56] is a sequence containing one integer, but is not an integer.(c) There are five integers in the sequence.
Exercise 2
Suppose that the variable till2 holds data in the form of a sequence of barcodes. When an item is read at the checkout, the state of till2 is changed by appending the barcode of the item to the end of the sequence giving the state of till2. Suppose that till2 currently has the state [50222, 50345], and that an item with barcode 50111 is read, and then an item with barcode 50456 is read. Write out the state of the variable till2 at each stage.
Answer
Solution
In turn, the state takes the following values:
| [50222, 50345] | (at the start). |
| [50222, 50345, 50111] | (after 50111 is read). |
| [50222, 50345, 50111, 50456] | (after 50456 is read). |
Exercise 3
With item prices as given in Table 1, what is the sequence of prices corresponding to the sequence of barcodes [33050, 33050, 77502, 53151, 77502]? What is the total price of the items given by this sequence?
Answer
Solution
The sequence of prices (given as integer numbers of pence, as in Table 1) is: [299, 299, 89, 440, 89]. The total price (in pence) is 1216 (or £12.16).
2 Forms of data
2.1 Numbers
The supermarket example discussed in Section 1 involves various forms of data that a computer may need to handle. Some of these, such as numbers and characters, are simple but fundamental. Other forms of data, such as sequences, involve more complicated structure. In this section, we will introduce sets, which are a variety of data collection that is different from sequences. But first we will look more carefully at numbers and characters.
When developing software we need to distinguish between different sorts of numbers, not least because computers represent and process them differently. Whole numbers (positive, negative or zero) are called integers. We shall use Int to denote the collection (or set) of all integers. In principle, digital computers can represent integers exactly, no matter how large or small. In practice, however, most programming languages place restrictions on the size of an integer (positive or negative) that can be stored. Many texts use ![]() instead of Int.
instead of Int.
Sometimes, we need to work with numbers that are not integers. Measured quantities, such as weights or distances, are often presented as non-integer values. More profoundly, even if one starts with whole numbers, some arithmetic processes, such as division or finding a square root, may yield results that are not integers (see Activity 3). The real numbers are a wider collection of numbers used in mathematics. A real number is conveniently thought of as a decimal, such as 435.5218 or –29.333344, but not every real number can be written as a decimal of a finite length. For example, √2 (the square root of 2) and the number ![]() (pi) are real numbers that are non-terminating decimals. Such numbers can never be expressed exactly as a finite decimal.
(pi) are real numbers that are non-terminating decimals. Such numbers can never be expressed exactly as a finite decimal.
![]() is approximately equal to 3.142. You may have met it in calculating the circumference or area of a circle.
is approximately equal to 3.142. You may have met it in calculating the circumference or area of a circle.
Digital computers cannot store real numbers exactly. They need to work with approximations to the real numbers. These approximations may be stored in the computer as floating point numbers. You can get a feeling for the sorts of issues that arise through the following example. Suppose (for the purposes of illustration) that we can only store a real number to an accuracy of four decimal places. Then the number 435.5218 might be stored as 0.4355 × 103. But 435.48336 (a different number) would also be stored as 0.4355 × 103.
If a software application really does need to deal with real numbers, then great care needs to be taken to ensure that the effects of (repeated) approximations are managed in a way that is well understood. This is especially true for safety critical applications, where people's lives may depend upon the behaviour of the software. However, in this course, we shall largely exclude further consideration of real numbers.
Activity 3
If x and y may each take any integer value, which of the following will always give an integer result and which may give a result that is not an integer? If you are not sure, try to choose values of x and y that do not give integer answers.
(a) x + y.
(b) x − y.
(c) x × y.
(d) x/y. (x divided by y.)
(e) x 2.
(f) √x.
Discussion
If x and y are integers, then (a) x + y, (b) x − y and (c) x × y will always be integers. In (e), x 2 means x × x, and if x is an integer then x 2 will be an integer. However, in (d), choosing x = 1 and y = 4 (both integers) gives ![]() or 0.25, which is not an integer. (In (d), if y is chosen to be 0, the result is undefined. Software that performs division should always ensure that division by 0 is not attempted.) In (f), choosing x = 8 (for example) gives √8, which is 2.828 (to an accuracy of 4 figures) and is not an integer.
or 0.25, which is not an integer. (In (d), if y is chosen to be 0, the result is undefined. Software that performs division should always ensure that division by 0 is not attempted.) In (f), choosing x = 8 (for example) gives √8, which is 2.828 (to an accuracy of 4 figures) and is not an integer.
2.2 Characters
Characters are another fundamental form of data. Computers store characters as integers, and system hardware and software translate these integer codes so that monitors and printers can display them.
As well as the familiar characters appearing on a keyboard, the current international standard (UNICODE) includes codes for characters from a variety of languages and alphabets (such as ê and ö). For simplicity, examples in this course will use only a part of this code, as given in Table 2. This is confined to printable symbols that appear on a standard computer keyboard (for an English-speaking user).
We will denote by Char the set of characters appearing in Table 2. We will call the codes in the table the ASCII codes of the characters.
The original ASCII set (developed by ANSI, the American National Standards Institute) was finalised in 1968, and provides a basic (but by no means complete) character set for English. With the development of the Internet and a more global economy, efforts are being made to create a standard character set, catering more completely for many languages, and bringing together hundreds of incompatible standards from different countries. UNICODE is the result of this development, but it still only represents some of the written characters of our languages, currently standing at about 94,000 symbols. No existing character set caters for all languages.
| Code | Character | Code | Character | Code | Character |
|---|---|---|---|---|---|
| 32 | 64 | @ | 96 | ' | |
| 33 | ! | 65 | A | 97 | a |
| 34 | " | 66 | B | 98 | b |
| 35 | # | 67 | C | 99 | c |
| 36 | $ | 68 | D | 100 | d |
| 37 | % | 69 | E | 101 | e |
| 38 | & | 70 | F | 102 | f |
| 39 | ’ | 71 | G | 103 | g |
| 40 | ( | 72 | H | 104 | h |
| 41 | ) | 73 | I | 105 | i |
| 42 | * | 74 | J | 106 | j |
| 43 | + | 75 | K | 107 | k |
| 44 | , | 76 | L | 108 | l |
| 45 | − | 77 | M | 109 | m |
| 46 | . | 78 | N | 110 | n |
| 47 | / | 79 | O | 111 | o |
| 48 | 0 | 80 | P | 112 | p |
| 49 | 1 | 81 | Q | 113 | q |
| 50 | 2 | 82 | R | 114 | r |
| 51 | 3 | 83 | S | 115 | s |
| 52 | 4 | 84 | T | 116 | t |
| 53 | 5 | 85 | U | 117 | u |
| 54 | 6 | 86 | V | 118 | v |
| 55 | 7 | 87 | W | 119 | w |
| 56 | 8 | 88 | X | 120 | x |
| 57 | 9 | 89 | Y | 121 | y |
| 58 | : | 90 | Z | 122 | z |
| 59 | ; | 91 | [ | 123 | { |
| 60 | 92 | \ |
124 | | | |
| 61 | = | 93 | ] | 125 | } |
| 62 | > | 94 | ^ | 126 | ˜ |
| 63 | ? | 95 | – |
The character with ASCII code 32 is the space character, which, when we need to write it explicitly, will appear as ‘![]() ’
’
Activity 4
(a) What character has ASCII code 91?
(b) What are the ASCII codes of the characters ‘A’ and ‘a’?
(c) What is the ASCII code of the character ‘7’?
Discussion
(a) The character ‘[’.
(b) 65 and 97, respectively.
(c) 55.
2.3 Truth values
We will want to distinguish between statements that are true and statements that are false. Another fundamental form of data allows us to do this. This form of data consists of just two values, which we shall write as true and false.
Not all texts use the same notation: some use T and F; others may use 0 for false and 1 for true (or the reverse!).
We may refer to true and false as truth values, or Boolean values. We will denote the collection (set) of truth values as Bool, after the mathematician George Boole. We write:
Bool = {true, false}.
This shows the collection Bool as a set. We have already mentioned the word set in passing, and now want to look at this concept in more detail.
2.4 Sets
A set is a collection of items, and is a collection of a particular form. The items appearing in a set are referred to as the elements (or members) of the set. Examples of sets mentioned earlier are: Int, Char and Bool.
A set is a collection in which repetition is not significant, nor is the order in which the items are given. For example, the supermarket might sell its own brand of Wheat Flakes in three sizes: large, medium and small. In a situation where we are interested in the types of product that are available, we are interested in the set of sizes. This set of sizes may be written as:
{large, medium, small}.
We might choose to name the set:
Sizes = {large, medium, small}.
The order in which the elements are listed is of no significance, so we might equally well have written Sizes = {small, medium, large}.
Notice the use of curly brackets {and} here. These are used as a signal that the collection is a set (as distinct from some other form of collection, such as a sequence). Note too the commas used to separate the elements.
We would not usually give any repetitions when writing a set, but if one were to do so, repetition of an element would be of no significance. We could write a set as
{large, small, large, medium, small}
but this set is the same as Sizes and has three members, not five!
We write a ∈ X to mean that the item a is a member of the set X (we say “a is in the set X”, or just “a is in X”). So, for example, we might write small ∈ Sizes.
It was easy to write out the set Sizes in full because it has only three elements. Imagine having to write out the set of all barcodes used at a large supermarket. It would not be practicable! We have another notation for such sets, that is sets whose members can be precisely described. Suppose that, a little unrealistically, a store (YtoZ Groceries) stocks just 90000 items, which happen to have barcodes that are consecutive integers between 10000 and 99999. Then the set of barcodes used by the store may be written:
YtoZBarcodes = { n ∈ Int : 10000 ≤ n and n ≤ 99999}.
A rather literal reading of this notation would be: “YtoZBarcodes is the set of values, n, in the set of integers, such that n is greater than or equal to 10000 and less than or equal to 99999.”. (We read the first curly bracket as “the set of” and the colon as “such that”.) More casually, we might say: “YtoZBarcodes is the set of integers between 10000 and 99999, inclusive.”. (The word inclusive makes it clear that the numbers 10000 and 99999 are each included in the set.)
Alternatively, the condition 10000 ≤ n and n ≤ 99999 can be written as 10000 ≤ n ≤ 99999.
A set need not have any members. (The set {n ∈ Int : n > 100 and n empty set. We will write this as { }.
Sometimes we need to say how many elements there are in a set. For example, the set Sizes, as above, has 3 elements, while the set YtoZBarcodes has 90000 members. The number of elements in a set is called the cardinality of the set. The cardinality of the empty set is 0. (We shall only talk about the cardinality of a finite set. The set Int, for example, does not have a finite number of elements.) If the members of a set have been written out with some elements repeated, then remember to count each repeated element only once when finding the set's cardinality. In other texts, you may see the symbol ∅ used to denote an empty set.
Activity 5
(a) Write out in full the set {n ∈ Int : 5 ≤ n and n
(b) Write out in full the set {c ∈ Char : the ASCII code of c is between 40 and 43, inclusive}.
(c) Which of the following is true?
(i) 7 ∈ Int.
(ii) ‘7’ ∈ Int.
(d) Let Lowercase = {c ∈ Char : the ASCII code of c is strictly greater than 96 and strictly less than 123}.
(i) Is ‘C’ ∈ Lowercase true?
(ii) What is the cardinality of the set Lowercase?
(e) Let A be the set of characters that appear in the string “aardvark”. What is the cardinality of A?
Discussion
(a) This set contains those integers that are both greater than or equal to 5, and strictly less than 9. We can write this set in full as {5, 6, 7, 8}. (Alternatively, it could be written with the elements in some other order, such as {8, 7, 5, 6}.)
(b) {‘(‘, ‘)’, ‘*’, ‘+’}. (Remember that we write characters in single inverted commas.)
(c) 7 is an integer, but ‘7’ is a character. So 7 ∈ Int is true, but ‘7’ ∈ Int is false.
(d) (i) The ASCII code of ‘C’ is 67 and so ‘C’ is not a member of the set Lowercase. So ‘C’ ∈ Lowercase is false.
(ii) There are 26 integers which are strictly greater than 96 and strictly less than 123. So Lowercase has cardinality 26.
(e) The set of characters that appear in the string “aardvark” is: {‘a’, ‘r’, ‘d’, ‘v’, ‘k’}. This set has cardinality 5.
2.5 Sequences
You have already met sequences briefly, and have seen that a sequence contains items given in a particular order, and that repetitions are of significance.
One might have a sequence containing integers, such as [22, −31, 44, 0, 2, 0, 11] or a sequence containing characters, such as [‘W’,‘o’,‘r’,‘d’]. However, we will aim to avoid mixing the forms of data in a sequence. A sequence of characters may also be referred to as a string, and that “Word” is another notation for the sequence [‘W’,‘o’,‘r’,‘d’].
The items in a sequence are enumerated from the left. Thus in the sequence [‘W’,‘o’,‘r’,‘d’], the first item is ‘W’, the second item is ‘o’, and so on. The items in a sequence may also be referred to as the elements (or sometimes members) of the sequence. The number of items in a sequence is called its length. So, for example, the length of the sequence [‘W’,‘o’,‘r’,‘d’] is 4.
We do count repeated items when calculating the length of a sequence. So, for example, the sequence of numbers [22, −31, 44, 0, 2, 0, 11] has length 7, while the sequence of characters “aardvark” has length 8.
Incidentally, we are only concerned in this course with finite sequences. If you study mathematics in other contexts, you may meet sequences that “go on forever”, such as the sequence of real numbers: 1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , ... (where the general term is
, ... (where the general term is ![]() where n is a positive integer). Any form of data stored on a computer as a sequence will contain a finite number of items, so a sequence describing a form of data stored on a computer will be finite. A finite sequence will have a length that is a positive integer.
where n is a positive integer). Any form of data stored on a computer as a sequence will contain a finite number of items, so a sequence describing a form of data stored on a computer will be finite. A finite sequence will have a length that is a positive integer.
Activity 6
(a) Let s be the sequence s = [44, 21, 77, 77, 41].
(i) What is the third member of s?
(ii) What is the fourth member of s?
(iii) What is the length of s?
(b) Let t be the sequence of characters t = “This sentence.”
(i) What is the fifth member of t?
(ii) What is the length of t?
(iii) What is the fifteenth member of t?
(c) Let A be the set of items appearing in the sequence s = [41, 21, 77, 77, 41]. What is the cardinality of A?
Discussion
(a)
(i) The third member of s is 77.
(ii) The fourth member of s is also 77.
(iii) The sequence s contains 5 items, so the length of s is 5.
(b)
(i) The fifth member of t is the space character, which we write as ‘
 ’.
’.(ii) The length of t is 14. (You need to count the space character and the full stop as well as the letters.)
(iii) There is no fifteenth character in t.
(c) The set A takes no notice of the order in which the items appear in s, nor of repeated items. The set A is {21, 41, 77}, and this has cardinality 3.
The set A could equally well be written as {41, 21, 77}, for example.
We have introduced notations for the set of all integers, Int, and for the set of characters, Char. It is convenient also to have a notation for sequences. This will need to tell us two things: first, that we are referring to a set of sequences; and second, the set from which the members of the sequence come. Thus we write SeqOfInt for the set of all sequences of integers. So, for example, [22, −31, 44, 0, 2, 0, 11] is in SeqOfInt. Similarly, we write SeqOfChar for the set of all sequences of characters. The sequence [‘W’,‘o’,‘r’,‘d’] is in SeqOfChar (and not in SeqOfInt), because it is a sequence that contains characters, not integers.
There are a couple of points to note here. First, the number 22 is not in SeqOfInt, because 22 is not a sequence, it is an integer. However, [22] is in SeqOfInt. This is a sequence that happens to contain just one integer. Second, both SeqOfInt and SeqOfChar include an empty sequence, [].
More generally, we write SeqOfX for the set containing all sequences of items from the set X. Here X might be any set. For example, SeqOfBool contains all sequences whose members are from Bool, that is, whose members are Boolean values.
Activity 7
(a)
(i) Is ‘a’ in the set SeqOfChar?
(ii) Is “a” in the set SeqOfChar?
(b) Give an example of a member of the set SeqOfBool.
Discussion
(a)
(i) No. The single quotes here show that ‘a’ is a character, from the set Char. Just as there is a distinction between a single integer such as 22 and a sequence containing one integer such as [22], there is a corresponding distinction between a single character and a sequence containing one character.
(ii) The double quotes here show we have a string; that is, a sequence of characters. So “a” is in SeqOfChar. The notation “a” means the same as [‘a’]: each is the sequence containing the single character ‘a’.
(b) A suitable example is [true, true, false, true], but there are an infinite number of possible examples (including, if you chose to be contrary, the empty sequence [ ], containing no Boolean values!).
2.6 Associations: tuples and Cartesian products
Consider an item of shopping that is weighed at the supermarket checkout, such as 335 grams of walnuts. This item of shopping has two features: the type of item purchased (walnuts), and the weight of that item (335 grams). To record a weighed item of shopping we need to note both these features. This can be done using an ordered pair: (“WALNUTS”, 335).
The first item in this ordered pair gives the type of item purchased. Let WeighedItems be the set of items stocked by the supermarket that need to be weighed. The first item comes from this set, while the second item in the ordered pair comes from the set Int.
We call the set containing all such pairs the Cartesian product of the two sets. (‘Cartesian’ after the famous French philosopher and mathematician René Descartes.) This set of pairs is written as WeighedItems × Int. So the set WeighedItems × Int consists of all pairs (w, n), where w comes from the set WeighedItems, and n comes from the set Int. We refer to (w, n) as an ordered pair. The word pair here indicates that there are two items grouped together. The word ordered indicates that the order in which the two items are given matters. The pair (“WALNUTS”, 335) is not the same as the pair (335, “WALNUTS”). Similarly, the set WeighedItems × Int is different from the set Int × WeighedItems, which consists of pairs giving: first an integer, then a type of weighed item.
Use of the symbol × here has nothing to do with multiplication of numbers!
We can form the Cartesian product of any two sets. The Cartesian product of sets X and Y is written as X × Y , and consists of all ordered pairs (x, y) where x is from the set X and y is from the set Y. X × Y can be read as “ X cross Y”.
An ordered pair gives an association between two items. There are situations where we may want to associate more than two things. Consider items stocked by the supermarket that have barcodes. The supermarket will be interested in a number of features associated with each item of this type. Three such features are:
The barcode (taken to be an integer).
The name of the item, to be printed on the till receipt (as a string).
The price of an item of this type (taken to be an integer number of pence).
A natural way to associate these three features is to write them together as an ordered triple, or 3-tuple, such as (13151, “ORGANIC SOUP”, 179). Note the use of round brackets here. These are used for tuples, in distinction to square brackets [ and ] for sequences, or curly brackets { and } for sets. The terminology ‘ordered triple’ indicates that we are now writing three items, each from a specified set, in a given order. We may want to associate four items, or five, or more. The terminology ‘tuple’ extends conveniently to this general case, where we talk about 4-tuples, or 5-tuples, and, in general, n-tuples (where n might be 2, or 3, or any larger integer).
The set of all 3-tuples of the same form as (13151, “ORGANIC SOUP”, 179) is again a Cartesian product, in this case a product of three sets. The barcode is from Int, the item name is a string (from SeqOfChar) and the price is an integer. So this 3-tuple comes from the set Int × SeqOfChar × Int.
Activity 8
Taking the code for olive oil as 43202, and referring to the receipt in Figure 2, write down the ordered triple from the set Int × SeqOfChar × Int that represents the association between the code, the description and the price of the olive oil.
Discussion
Making sure that the description is written as a string, and that the price is in pence, the triple should be (43202, “OLIVE OIL”, 178).
As another example, suppose that a shop has just three members of staff, Jo, Jessica and Wesley, and just two tills, T1 and T2. We could represent a situation where Jo is operating the till T2 by the ordered pair, or 2-tuple (T2, Jo). Clearly, there are a variety of ways in which a member of staff can be assigned to a till. If Tills is the set {T1, T2} and Staff is the set {Jo, Jessica, Wesley}, then the set of all possible assignments of a member of staff to a till is Tills × Staff . If we write this set out in full, we obtain:
Tills × Staff = {(T1, Jo), (T1, Jessica), (T1, Wesley), (T2, Jo), (T2, Jessica), (T2, Wesley)}.
Note the use of different brackets: curly brackets delimit the set, round brackets delimit each of the tuples. Note also that the use of Tills × Staff to represent assignment of a staff member to a till means that we must write the till first in each ordered pair.
Activity 9
(a) Give an example of a member of the set Staff × Tills.
(b) If the supermarket were to install another till, and recruit two more members of staff, and we redefine the sets Staff and Tills to include these, how many ordered pairs would be in the set Tills × Staff?
Discussion
(a) In Staff × Tills, the member of staff should be given first. Suitable examples would be (Jo, T1), or (Wesley, T2).
(b) There would then be 3 tills and 5 staff. Each till can appear with each member of staff in an ordered pair, so there would be 3 × 5 = 15 ordered pairs in Tills × Staff.
Objectives for Section 2
After studying this section you should be able to do the following.
Recognise and use the terminology: real number; set; element or member of a set; empty set; length of a sequence; empty sequence, ordered pair, n-tuple, Cartesian product.
Appreciate that use of precise notation such as the use of different types of bracket conveys important information when using formal notation. For example, square brackets [ and ] denote a sequence, while curly brackets { and } denote a set.
Use and interpret various pieces of notation:
curly brackets to denote a set;
– definition of a set by using a condition;
{ } to denote the empty set;
[ ] to denote an empty sequence;
SeqOfX to denote the set of all sequences with members from X;
(x, y) to denote an ordered pair or 2-tuple; (x, y, z) to denote a 3-tuple, etc.;
X × Y to denote the Cartesian product of the sets X and Y .
Determine the cardinality of a given set and the length of a given sequence.
Given i, determine the ith element of a given sequence.
Be aware of the ASCII character codes.
Appreciate that some sets are finite and some are not.
Exercises on Section 2
Exercise 4
Let A be the set of integers between 100 and 999 inclusive.
(a) Express A in the form A = {x ∈ ?? : condition}
(b) What is the cardinality of A?
Answer
Solution
(a) A = {x ∈ Int : 100 ≤ x and x ≤ 999}. (There are other correct solutions.)
(b) There are 999 integers between 1 and 999 inclusive. The set A does not contain the integers between 1 and 99 inclusive, and there are 99 of these. So A has cardinality 999 − 99 = 900.
Exercise 5
If B = {s ∈ SeqOfChar : s starts with ‘T’ and s has length 4}, which of the following is a member of the set B?
(a) “This”.
(b) [‘T’, ‘h’, ‘i’, ‘s’, ‘.’].
(c) [“T”, “h”, “i”, “s”].
Answer
Solution
(a) “This” is in B. It is a string (a sequence of characters), it contains four characters (so has length 4), and it starts with the character ‘T’.
(b) [‘T’, ‘h’, ‘i’, ‘s’, ‘.’] is not in B. It is a string starting with ‘T’, but it contains five characters (has length 5). (Do not forget to count the character ‘.’.)
(c) [“T”, “h”, “i”, “s”] is not in B. Each member of this sequence is a string, not a character. (Note that “T”, etc, are enclosed in double inverted commas.)
Exercise 6
Suppose that each possible time of the day is stored as a pair of integers, where the first integer gives the hour and the second integer gives the minute. For example, (14, 45) represents a quarter to three in the afternoon. (Midnight is (0, 0) rather than (24, 00).) Express the set of possible times of the day in the form {(h, m) ∈ ?? : condition}.
Answer
Solution
The set is {(h, m) ∈ Int × Int : 0 ≤ h and h m and m
3 Combining forms of data
Structuring data
In Section 2, we considered integers, characters and truth values. We shall refer to these as primitive forms of data. We also looked at two forms of data collection, sets and sequences, and at the association of different data items in a tuple. In this section, we will look briefly at some other ways in which data may be structured.
3.1 Sets of sets
In Section 2, all the sets and sequences we considered had primitive forms of data as their elements. However, sets and sequences may contain non-primitive forms of data. Let us look first at a situation in which we may find it useful to have a set whose members are themselves sets.
Think again about a shop with just three members of staff, given in the set Staff = {Jo, Jessica, Wesley}. Now let at WorkStaff be the set of staff currently at work. Clearly, at WorkStaff may take a range of values. If just Jo and Wesley are at work, then at WorkStaff is {Jo, Wesley}. If Jessica were to start work and Jo were to leave, then at WorkStaff becomes {Jessica, Wesley}.
Now any combination of staff from the set Staff = {Jo, Jessica, Wesley} might be at work at the same time. Possibilities include all these staff (when at WorkStaff is {Jo, Jessica, Wesley}), and none of them (in which case at WorkStaff is { }). The full list of possibilities (giving the possible values of at WorkStaff ) is given below.
{ }, {Jo}, {Jessica}, {Wesley}, {Jo, Jessica}, {Jo, Wesley}, {Jessica, Wesley}, {Jo, Jessica, Wesley}
Here, we have written out all the sets with members taken from the set Staff = {Jo, Jessica, Wesley}. We can form a set whose members are these sets. We will denote this set by SetOfStaff . So:
SetOfStaff = {{ }, {Jo}, {Jessica}, {Wesley}, {Jo, Jessica}, {Jo, Wesley}, {Jessica, Wesley}, {Jo, Jessica, Wesley}}.
The outer curly brackets here delimit the members of the set SetOfStaff. Each of these members is itself a set, and the inner curly brackets delimit each of these member sets. We will not often need to list the members of a set of sets like this. But it is useful to be aware that we can form a set in this way. We might have a variable atWorkStaff, giving the set of staff currently at work. The set giving all possible states of this variable is then SetOfStaff.
In general, we will use SetOfX to denote the set consisting of all the sets drawn from some given set, X. SetOfX is also known as the power set of X. Various other notations are used for this, including P(X) and 2X . The latter is sometimes used since, if X has cardinality n, then SetOfX has cardinality 2n . For example Staff has cardinality 3 and SetOfStaff has cardinality 8, which is 23.
Activity 10
Suppose that the set of tills in a supermarket is Tills = {T1, T2, T3} and active Tills is a variable giving the set of tills that are staffed at any one time. Write out in full the set of possible states for active Tills.
Discussion
The set of possible states is the set SetOfTills. Written in full, this is:
{{}, {T1}, {T2}, {T3 }, {T1, T2}, {T1, T3}, {T2, T3}, {T1, T2, T3}}.
3.2 Combining data structures
In Section 2, we introduced the notation SeqOfX for the set of all sequences whose members come from the set X. In Section 2, we looked only at sequences whose members were of one of the primitive forms of data (integers, characters or Booleans). We can have sequences whose members are themselves data with a more complicated form. For example, suppose that Jo is working at the till T1 and is replaced by Jessica. We might represent this handover by the 3-tuple (Jo, T1, Jessica). Now suppose that we want to give all the handovers that occur during a particular day, in the order in which they occur. We could give this information in a sequence. This sequence would come from the set SeqOfX , where X is the Cartesian product Staff × Tills × Staff.
As another example, one might think of a sentence as a sequence of words, where each word is seen as a sequence of characters. If we did this, then the sentence would be regarded as coming from the set SeqOfSeqOfChar. We can use notations introduced earlier to show when we want to see a sentence in this way, and when it is to be regarded as a single string (from SeqOfChar).
Activity 11
Which of the following is a member of the set SeqOfSeqOfChar?
(a) [‘W’,‘o’,‘r’,‘d’].
(b) “This is a sentence.”.
(c) [“This”,“is”,“a”,“sentence”].
Discussion
Only (c) is a member of SeqOfSeqOfChar.
(a) This is a sequence of characters and so a member of SeqOfChar.
(b) This is a string, so is again a sequence of characters (written in our more compact notation).
(c) This is a sequence each of whose members is a string. Thus each item in the sequence in (c) comes from SeqOfChar. The sequence itself comes from SeqOfSeqOfChar.
Consider a computer system which has a finite set of error messages, each of which may be displayed to a cashier at the till. Suppose these messages are: “Barcode error”; “Item code not recognised” and “System error 1234”. This set of error messages can be represented thus:
Errors = {“Barcode error”, “Item code not recognised”, “System error 1234”}.
Each of these messages is given as a string, that is, as a sequence of characters. So Errors is a set of sequences of characters.
3.3 Mixing different forms of data: disjoint union of sets
At the supermarket checkout, some items need to be weighed (organic courgettes for example) and some do not. Let BarcodedItems be the set of items that do not need to be weighed, and WeighedItems be the set of items that must be weighed. When a weighed item is recorded at the till, we must record both the item type and the weight of the item that has been purchased. Earlier, we saw that such a purchase can be seen as an ordered pair, such as (“WALNUTS”, 335), that comes from the set WeighedItems × Int.
Suppose now that we want to form the set of all items that might appear in a transaction at a till. We might call this set TillItems. Specifying this set TillItems poses a complication, since there are two different types of element that might appear in it. An item from the set TillItems will come either from BarcodedItems or from WeighedItems × Int. We express this relationship by saying that TillItems is the disjoint union of BarcodedItems and WeighedItems × Int. We write this as:
You can read X ![]() Y as “X or Y.”
Y as “X or Y.”
TillItems = BarcodedItems ![]() (WeighedItems × Int).
(WeighedItems × Int).
In general, the disjoint union of sets X and Y , written X ![]() Y , is the set consisting of all items that are either from X or from Y . The term “disjoint” reflects the fact that an item could not come both from BarcodedItems and from WeighedItems × Int. These sets contain different forms of data and have nothing in common. (We will only use disjoint union to combine sets containing different forms of data.)
Y , is the set consisting of all items that are either from X or from Y . The term “disjoint” reflects the fact that an item could not come both from BarcodedItems and from WeighedItems × Int. These sets contain different forms of data and have nothing in common. (We will only use disjoint union to combine sets containing different forms of data.)
As in Section 1, suppose that till1 is a variable representing a transaction in progress at till 1. The state of till1 will give the items recorded so far, in the order in which they were entered into the till, either by reading the barcode, or as a weighed item. So we can describe the state of till1 as a sequence of till items. The set of all possible states of till1 is SeqOfTillItems, where TillItems is BarcodedItems ![]() (WeighedItems × Int).
(WeighedItems × Int).
As noted earlier, we usually want to avoid mixing data of different forms in a collection such as a sequence. But if we need to do this, we can first use a disjoint union to combine the different forms of data into a single set. So, for example, if we needed to form a sequence whose members might be either characters or integers, then this sequence would come from a set SeqOfMix, where Mix is the disjoint union Int ![]() Char.
Char.
Activity 12
Let TillItems = BarcodedItems ![]() (WeighedItems × Int), and suppose that BarcodedItems is represented as the set of integers between 10000 and 99999 and WeighedItems as the set of integers between 100 and 999. Which of the sequences given in (a)–(c) below is a member of the set SeqOfTillItems?
(WeighedItems × Int), and suppose that BarcodedItems is represented as the set of integers between 10000 and 99999 and WeighedItems as the set of integers between 100 and 999. Which of the sequences given in (a)–(c) below is a member of the set SeqOfTillItems?
(a) [1, −740, (22, 300)]
(b) [11, ‘2’, ‘w’, 33000, −22]
(c) [11023, 11023, (998, 12), 22375, (217, 147)]
Discussion
Only the sequence in (c) is in SeqOfTillItems.
(a) According to the statement, a barcoded item is represented by an integer with five digits. So 1 and −740 are not from the set BarcodedItems.
(b) This sequence contains some characters, which are neither from the set BarcodedItems nor from WeighedItems × Int.
(c) Each of the integers 11023 and 22375 lies between 10000 and 99999, and so comes from the set BarcodedItems. The first entry in each of the pairs (998, 12) and (217, 147) is an integer between 100 and 999, so comes from WeighedItems. Thus each of these ordered pairs comes from WeighedItems × Int. So each item in the sequence is either from BarcodedItems or from WeighedItems × Int, and so comes from TillItems.
3.4 Representing data in applications
Suppose that you are designing software for some application. You will be working with a programming language that enables you to communicate instructions to a computer. In this programming language, certain forms of data will already be represented electronically. These will include common forms of data, such as numbers, characters and sequences. In any particular application, you are likely also to be concerned with forms of data that are peculiar to that application. Having identified some form of data that you need to be able to handle, you will then need to represent this in terms of what is available; that is, in terms of forms of data that have already been represented electronically.
As a simple example, imagine that integers, characters and strings are available forms of data, and that you want to represent the days of the week.
One natural form of representation is as strings: “Monday”, “Tuesday”, “Wednesday”, and so on. But other forms of representation are possible. The full names can be inconvenient because they involve a lot of writing, so one might choose to use shortened versions, such as: “Mon”, “Tues”, “Wed”, etc. We could be awkward (from the viewpoint of an English speaker), and use the strings: “Lundi”, “Mardi”, “Mercredi”, and so on. Or we could use integers, and represent Monday as 1, Tuesday as 2, Wednesday as 3, etc. This might be very convenient at times, but one then needs to remember which number represents which day.
There are times when it is important to distinguish between a form of data derived from an application situation and the concrete representation you have chosen for it. We might refer to the idea of the days of the week as an abstraction, in distinction to their representation, perhaps as the strings “Mon”, “Tues”, “Wed”, etc.
Activity 13
A compact form of representation for days of the week might be to use the first character of the name: ‘M’ for Monday, ‘T’ for Tuesday, and so on. Why would this be a bad idea?
Discussion
Because we could not tell whether ‘T’ meant Tuesday or Thursday (or whether ‘S’ meant Saturday or Sunday). Different entities in the abstract set of application data need to have different representations.
One additional point of importance about any form of data in an application concerns the ways in which we need to be able to manipulate it. We turn to processes on data in the next section.
Objectives for Section 3
After studying this section you should be able to do the following.
Recognise and use the terminology: disjoint union; power set (of a set); representation (of a data abstraction).
Use and interpret the notation:
X
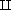 Y for the disjoint union of the sets X and Y ;
Y for the disjoint union of the sets X and Y ;SeqOfSetOfInt for the set consisting of all sequences whose members are sets of integers (and similar notations).
Exercises on Section 3
Exercise 7
Each of (a)–(c) is a member of one of the sets given in (i)–(iii). Say which item comes from which set.
Sets: (i) SetOfSeqOfChar. (ii) SeqOfSetOfChar. (iii) SeqOfSeqOfChar.
(a) {“error1”, “error2”, “error3”}.
(b) [“error1”, “error2”, “error3”].
(c) [{‘e’,‘1’}, {‘T’}, {‘q’,‘w’,‘e’,‘r’,‘t’,‘y’}].
Answer
Solution
(a) This is a set, as shown by the outer curly brackets. Each member of this set is a string, that is, a sequence of characters. So (a) is a set of sequences of characters. It is a member of SetOfSeqOfChar.
(b) This is a sequence, as shown by the outer square brackets. It is a sequence of strings. So (b) is a sequence of sequences of characters. It comes from SeqOfSeqOfChar.
(c) This is again a sequence. Each member of this sequence is a set of characters. So (c) comes from SeqOfSetOfChar.
Exercise 8
Let Mix be the disjoint union Int ![]() Char. What is the length of the following sequence from SeqOfMix?
Char. What is the length of the following sequence from SeqOfMix?
[555, ‘5’, ‘5’, ‘5’, 11, 1].
Answer
Solution
There are six items in the sequence [555,‘5’,‘5’,‘5’,11,1] (three integers and three characters), so the length of this sequence is 6.
4 Processes
Processes that can be applied to data
Having looked at some forms of data, we now turn our attention to processes that can be applied to data. Each process that we consider in this section will input data of a specified form, and will result in a corresponding value. For example, one process, which we will call ASC, takes a character as input, and has as its resulting value the integer giving the ASCII code of the input character (as listed in Table 2). Another process, which we will call SIZE, takes a sequence as input, and has as its resulting value the length of the sequence (which will be an integer).
It is important to distinguish between a description of the outcome required when a process is applied to a form of data, and a description of the exact steps to be taken to achieve the desired outcome. Here, we are concerned only with the first of these; that is, with providing an overview of a computing process. You might like to think of this as a “black box” view of the process. We do not, at this stage, care how one obtains the output value.
Certain processes change the state of a named variable. For now, though, we shall not think about processes in that way. Each process that we are concerned with here simply produces a value that depends on one (or more) input value(s). Another important feature of the processes that we shall consider is that they result in a value that is entirely predictable. One can envisage a process that takes a string as input, and which results in a value that is a character that appears in the string. With input “This”, the value resulting from such a process might be any of the four characters ‘T’, ‘h’, ‘i’ or ‘s’. We will not consider a process such as that. Our attention will be confined to processes that, if given the same input twice, will produce the same resulting value each time.
Below, we give a number of examples of processes that may be applied to numbers, characters or sequences. Focus first on Example 1(a) below This process is applied to an input, comprising data of a specified form (a sequence of integers). Application of the process results in a value (the sum of the integers in the input sequence). This resulting value will be referred to as the value returned by the process. Similar comments apply to each of these examples. Each process takes data of a specified form as an input, and each process returns a value, based on this input data. The returned value may also be called the output of the process.
Example 1
(a) Given a sequence of integers, return the sum of all the numbers in the sequence. For example, given [6, 2, 5, 6] the value returned is 19.
(b) Given a string, return the first upper-case letter that appears in the string. For example, given the string “my name is Bob”, the value returned is ‘B’.
(c) Given a string, return the first character in the string. For example, given the string “This is a sentence.”, the value returned is ‘T’.
(d) Given some integer, x, say, return the integer x 2 + x. For example, given the number 4, the value returned is 42 + 4 = 20.
(e) Given a sequence of items from a set X, and another item from the set X, return the sequence formed by placing the item at the end of the sequence. For example, given the sequence of integers [6, 2, 5, 6] and the integer 1, the value returned is [6, 2, 5, 6, 1].
(f) Given a string and a character, return the position in the string where the given character first occurs (counting characters from the front of the string). For example, if the string “This is a sentence.” and the character ‘s’ are given, then the value returned is 4, since the first occurrence of ‘s’ in the string is at the fourth place in the sequence [‘T’,‘h’,‘i’,‘s’,‘
 ’,‘i’,‘s’, . . . ].
’,‘i’,‘s’, . . . ].
Here are some key questions to consider about each process.
How many inputs are required, and of what type?
What type of value does the process return?
What is the relationship between the returned value and the input(s)?
Are there any restrictions on the input(s)?
Does the process always produce an output? Given any permitted input, is there an associated returned value?
Is the output produced predictable? Given the same input, will the process always return the same value?
For example, consider Example 1(b) above. In that case the questions can be answered as follows. The process has just one input and this is a sequence of characters. It outputs a character. The output value is the first upper-case letter that appears in the sequence of characters. For this description of the output to yield any value, the input sequence needs to contain at least one upper-case letter. Given that restriction on the input, there will always be an output. The output is predictable.
4.1 Functions
A function is a process that, when given an input of a specified type, yields a unique output. This is a key idea in providing a precise, mathematical, description of processes in computing.
To describe a particular function, we first give the set from which the input will be drawn and the set from which the output is drawn. This information is called the signature of the function. An example will make this clearer. Example 1(b), on the previous screen, requires an input that is a string, that is, a sequence of characters. The set containing all possible sequences of characters is SeqOfChar. Example 1(b) produces an output that is a character, so this output is in the set Char. We write the signature of this function as SeqOfChar → Char. The set to the left of the arrow is called the input set of the function and the set to the right is called the output set. Some texts use source set rather than input set, and target set rather than output set. It is usual to include an identifier for the function itself in the signature. Suppose we call this function FIRSTCAP. Then its full signature is:
FIRSTCAP: SeqOfChar → Char.
SeqOfChar comprises all sequences of characters, and so includes some sequences that have no upper-case letters.
The second piece of information required in describing a function is any restriction on the input(s). The informal description of FIRSTCAP states only that the first upper-case letter is returned. It does not specify what happens if there is no upper-case letter in the input. Accordingly, a sensible condition on the set of inputs to FIRSTCAP is that the input sequence must contain at least one upper-case letter. This condition on the input value is called the precondition of the function FIRSTCAP.
The third and final piece of information required is the relationship between output and input values. This relationship is referred to as the semantics of the function. The semantics must ensure that there is a unique output for any given input. We can describe the function FIRSTCAP like this:
FIRSTCAP has signature SeqOfChar → Char; its input sequence must contain at least one upper-case letter, and it returns the first upper-case letter appearing in the input sequence.
However, it is not always easy to extract key pieces of information from such a description. We shall usually describe functions using a standard layout, as in the description of FIRSTCAP given below. In exercises, to signal that we want the description of a function to be laid out as below, we will ask for a full description of the function.
function FIRSTCAP(s in SeqOfChar) return in Char
pre s contains at least one upper-case letter.
post The returned value is the first upper-case letter appearing in s.
The signature of the function FIRSTCAP is implicit in the first line of this description. (The signature is FIRSTCAP : SeqOfChar → Char.) This line shows that the function has an input (with identifier s) that comes from SeqOfChar. So its input set is SeqOfChar. The function returns a value in Char. So its output set is Char. We refer to the first line in the full description as the signature line.
The input value s must satisfy the condition given in the line starting pre. This line gives the precondition of the function. The semantics of the function are given in the line starting post. The statement in this line is referred to as the postcondition of the function.
Here, “pre” and “post” are used in the sense of “before” and “after”. Before FIRSTCAP can be applied to a value, that value must satisfy the precondition. After FIRSTCAP has been applied, the returned value will satisfy the postcondition.
Sometimes, we want to refer to the set of input values for which a function is defined. This is called the domain of the function, and is the set of values in the input set that satisfy the precondition of the function.
A function that is defined for all elements in its input set is called a total function. For a total function, no precondition is required on the input value (beyond requiring that it is in the input set). We show this by writing pre true (since the precondition is automatically true).
As another example, consider the process 4.1(d) given earlier. It stated:
given some integer, x, say, return the integer x 2 + x.
A full description of this function is given below. We will give it the identifier FORMULA. The rule for producing an output works for any integer, so we can write true for the precondition.
function FORMULA(x in Int) return in Int
pre true.
post The returned value is x 2 + x.
Activity 14
(a) Call the function associated with Example 1(c) on the previous screen, FIRSTCHAR. Give the signature of this function. Write out a full description of it.
(b) Suggest a full description of a function SUMSEQ, associated with the Example 1(a).
Discussion
Suitable descriptions are given below.
(a) FIRSTCHAR inputs a string (sequence of characters), and returns a character. So its signature is FIRSTCHAR : SeqOfChar → Char. To have a “first character”, the input sequence needs to contain at least one character, so the function needs a corresponding precondition.
function FIRSTCHAR(s in SeqOfChar) return in Char
pre s contains at least one character.
post The returned value is the first character appearing in s.
The choice of identifier for the input is arbitrary. You may well have used some identifier other than s in your answer.
(b) Note that SUMSEQ inputs a sequence of integers, and returns an integer. A suitable description is given below.
function SUMSEQ(s in SeqOfInt) return in Int
pre true.
post The returned value is the total of the numbers appearing in s. If s contains no members, then the returned value is 0.
You might have chosen to say that the input sequence should not be empty, since the idea of “the total of the numbers” might seem unclear if there are no numbers to add up! That would be fine. We have chosen to regard the “total of no numbers” as 0, and have said so explicitly in the semantics. Sometimes, one needs to make more precise an informal idea of a process. Deciding whether to add a precondition, or to explain what happens in special cases, is the sort of clarification that may be needed.
The value obtained when some function F is applied to an input x is written F(x). So, for example, FIRSTCAP(“a1wQ2*”) means the result of applying the function FIRSTCAP to the string “a1wQ2*”. The value obtained in that case is the first upper-case letter in “a1wQ2*”, and so is ‘Q’.
The example process 1(f), given earlier, was:
Given a string and a character, return the position in the string where the character first occurs.
For example, if the string “This is a sentence.” and the character ‘s’ are given, then the value returned is 4. This function requires two inputs: a string (a sequence of characters), and a character. We can describe the function as below.
function FIRSTAT(c in Char,t in SeqOfChar) return in Int
pre The character c appears at least once in the sequence t.
post The returned value is the integer n satisfying the condition that the nth character in the sequence t is c, and this is the first occurrence of c in t.
Where a function requires more than one input, the input set is taken to be a Cartesian product of sets, one for each input. For this example, the input set is Char × SeqOfChar. The output set is Int, so the signature of the function is FIRSTAT : Char × SeqOfChar → Int.
We can, for example, apply this function in the form
FIRSTAT(‘s’, “This is a sentence.”). However, we cannot apply it in the form FIRSTAT(“This is a sentence.”, ‘s’). The order of the two inputs given in the signature line in the description of FIRSTAT must be adhered to.
(We could have described a function accepting the inputs in a different order, with the sequence first and the character second. But this would be another function, different from FIRSTAT, just as reversing the order in which two sets are written in a Cartesian product produces a different set.)
Look now at Example 1(e), repeated below.
Given a sequence of items from a set X, and another item from the set X, return the sequence formed by placing the item at the end of the sequence. For example, given the sequence of integers [6,2,5,6] and the integer 1, the value returned is [6,2,5,6,1].
Note that this description is not confined to sequences of numbers. It can be used for sequences with members from any set. This general set is represented here by X. We can describe a function ADDLAST corresponding to this process as below.
function ADDLAST(x in X , s in SeqOfX ) return in SeqOfX
pre true.
post The returned value is formed by placing the item x at the end of the sequence s. For example, ADDLAST(1,[6, 2, 5, 6]) = [6, 2, 5, 6, 1].
Activity 15
(a) Give the signature of the function ADDLAST.
(b) What are the values:
(i) ADDLAST(7,[1, 4, 3, 2]);
(ii) ADDLAST(‘y’,“qwert”);
(iii) ADDLAST(“qwert”,‘y’)?
Discussion
(a) The signature is ADDLAST : X × SeqOfX → SeqOfX . (The order of the sets in the Cartesian product corresponds to the order of the inputs given in the description above.)
(b) We have:
(i) ADDLAST(7, [1, 4, 3, 2]) = [1, 4, 3, 2, 7];
(ii) ADDLAST(‘y’, “qwert”) = “qwerty”;
(iii) ADDLAST(“qwert”,‘y’) cannot be formed. The inputs are given in the wrong order.
Activity 16
This activity concerns the three functions on sequences given below. In each case, the sequence members come from an arbitrary set, X. You will meet these functions again later in the course.
A function SIZE, which, given a sequence, returns the number of members in it (that is, it returns the length of the sequence). So, for example, SIZE([1, 11, −32, 4, 12, 1]) = 6.
A function AT, which returns the item that is at a specified position in a sequence. So, for example, AT(4, “author”) = ‘h’.
A function PUT, which replaces the item that is at a specified position in a sequence with an item supplied as an input. So, for example, PUT(4,“author”,‘q’) = “autqor”.
(a) Give the values of:
(i) SIZE(“author”);
(ii) AT(3,[1, 11, -32, 4]);
(iii) PUT(3,“paan”,‘i’);
(iv) PUT(2, [1, 8, 2, 4], 3).
(b) Give the signature of each of the three functions.
(c) Give full descriptions of each of the three functions.
Discussion
(a) (i) 6 (the number of characters in the string “author”).
(ii) −32 (the third item in the sequence [1, 11, −32, 4]).
(iii) We replace the character at the third place in the string “paan” by the input character ‘i’, to get “pain”.
(iv) The first number gives the position of the item to be changed and the final number is the replacement item. So the value is [1, 3, 2, 4].
(b) SIZE has one input, from SeqOfX , and returns a value in Int. The signature is SIZE : SeqOfX → Int.
The function AT inputs an integer and a sequence and returns a value from X, so the signature is AT : Int × SeqOfX → X.
For the function PUT, the input set is a Cartesian product of three sets, one for each of the three inputs.
The signature is PUT : Int × SeqOfX × X → SeqOfX .
(c) Suitable descriptions are given below.
For SIZE, recall that the number of elements in the empty sequence is 0, so this is a total function.
function SIZE(s in SeqOfX ) return in Int
pre true.
post The returned value is the number of items in the sequence s. If s contains no members then the returned value is 0.
For AT, the semantics only make sense if the integer input gives a position actually in the sequence. So we give a precondition that the input integer is at least 1 (when the first item in the sequence will be returned), and that the input integer is not bigger than the number of items in the sequence. If we use another function in a description, as we use SIZE here in describing AT, then we must describe that function too. SIZE was described above.
function AT(i in Int, s in SeqOfX ) return in X
pre 1≤ i and i≤ SIZE(s).
post The returned value is the ith item in the sequence s.
The function PUT has three inputs, an integer (giving the position of the item to be changed), the sequence to be modified, and the replacement item (from the set X). It requires the same precondition as AT.
function PUT(i in Int, s in SeqOfX , x in X ) return in SeqOfX
pre 1 ≤ i and i ≤ SIZE(s).
post The returned value is the sequence formed by replacing the ith item in s by x.
4.2 Functions defined through cases
In each of the examples considered so far, the function has had its semantics expressed using a formula or a general rule. Some functions have their semantics expressed simply by listing the output for each possible input. For example, let Days be the set of days of the week, and the function TOMORROW have signature Days → Days, and return the day following the input day. If we represent Days using the strings {“Mon”, “Tues”, “Wed”, “Thurs”, “Fri”, “Sat”, “Sun”}, then we can describe the corresponding representation of the function TOMORROW as below.
function TOMORROW1(d in SeqOfChar) return in SeqOfChar
pre d is in the set {“Mon”,“Tues”,“Wed”,“Thurs”,“Fri”,“Sat”,“Sun”}.
post The returned value is t, where:
if d = “Mon” then t = “Tues”
if d = “Tues” then t = “Wed”
if d = “Wed” then t = “Thurs”
if d = “Thurs” then t = “Fri”
if d = “Fri” then t = “Sat”
if d = “Sat” then t = “Sun”
if d = “Sun” then t = “Mon”.
We distinguish the abstraction (the function TOMORROW) from its representation (the function TOMORROW1), because different representations of the set Days will lead to different representations of the function TOMORROW (see, for example, Exercise 2).
Activity 17
Suppose that a particular breakfast cereal is sold in sizes Small, Medium and Large, and that we choose to represent these by the characters ‘S’, ‘M’ and ‘L’. Their respective prices, in pence, are 89 for ‘S’, 119 for ‘M’ and 159 for ‘L’. Describe a function CEREALPRICE that takes a size as input and returns the associated price.
Discussion
We can describe this function as follows.
function CEREALPRICE(c in Char) return in Int
pre c is in the set {‘S’, ‘M’, ‘L’}.
post The returned value is p, where:
if c = ‘S’ then p = 89
if c = ‘M’ then p = 119
if c = ‘L’ then p = 159.
4.3 Character code functions
Many programming languages provide two functions associated with the character codes (see Table 2). We shall call these functions ASC and CHR. ASC takes a character as input, and returns the integer giving the ASCII code of the input character. CHR returns the character whose ASCII code is the input integer. These functions are described below. We have set a precondition on CHR to conform to our earlier restriction on the set of characters that we will consider in this course.
function ASC(c in Char) return in Int
pre true.
post The returned value is the ASCII code of c, as given in Table 2.
function CHR(n in Int) return in Char
pre 32 ≤ n ≤ 126.
post The returned value is the character with ASCII code n, as given in Table 2.
Activity 18
Find each of:
(a) ASC(‘j’);
(b) CHR(43);
(c) ASC(CHR(43));
(d) CHR(ASC(‘j’)).
Discussion
(a) Referring to Table 2, ASC(‘j’) = 106.
(b) CHR(43) = ‘+’.
(c) ASC(CHR(43)) means the result of applying the function ASC to CHR(43). So ASC(CHR(43)) = ASC(‘+’) = 43.
(d) CHR(ASC(‘j’)) = CHR(106) = ‘j’.
Looking up the ASCII code of a character, and then looking to see the character corresponding to the number you just found, will always take you back to the character you started with. We can express this in a general equation, as CHR(ASC(c)) = c. (This holds for any character c.)
As illustrated in Activity 18, the two functions ASC and CHR are closely related. Each reverses the effect of the other. We can express this relationship by writing the two equations below (which hold for every c in Char and for every n in Int satisfying the condition 32 ≤ n ≤ 126).
ASC(CHR(n)) = n
CHR(ASC(c)) = c
We say that ASC and CHR are inverse functions.
Not every function can be paired up with an inverse function in this way. For example, the function FIRSTCHAR returns the first character in a string. Now different strings may have the same first character. (“This” and “The” both start with ‘T’, but are different strings.) With input ‘T’, a process attempting to reverse the effect of FIRSTCHAR would not know whether to return “This” or “The” (or “To”, or “Tom”, etc). The function FIRSTCHAR has no inverse function.
Activity 19
A simple cipher replaces each lower-case letter with the next one in alphabetical order. So ‘a’ is replaced by ‘b’, ‘b’ by ‘c’,. . . , ‘t’ by ‘u’, and so on. The letter z ‘ ’ is replaced by ‘a’. The function NEXT, specified below, corresponds to this coding.
function NEXT(c in Char) return in Char
pre c is a lower-case letter.
post If c lies between ‘a’ and ‘y’ then the returned value is the letter following c in alphabetical order. If c = ‘z’ then the returned value is ‘a’.
Does the function NEXT have an inverse function? If it does, describe this inverse function.
Discussion
We can reverse the effect of NEXT by moving each character back one place in alphabetical order. This time, the special case is ‘a’, which must be moved to ‘z’. So NEXT does have an inverse function. If we call it BEFORE, it can be described as below.
function BEFORE(c in Char) return in Char
pre c is a lower-case letter.
post If c lies between ‘b’ and ‘z ’ then the returned value is the letter preceding c in alphabetical order. If c = ‘a’ then the returned value is ‘z’.
4.4 Functions returning true or false
Consider a function, say ISIN , associated with following process.
Given a character and a string, determine whether the character appears in the string.
This function has two inputs, a character and a string (sequence of characters), so we can take the input set to be Char × SeqOfChar. But what is the output set? If the character does appear in the string, then the function can return the value true, and if the character does not appear in the string, then the function can return the value false. So a suitable output set is Bool. Then ISIN has signature Char × SeqOfChar → Bool. We can describe the function ISIN as below.
function ISIN (c in Char, s in SeqOfChar) return in Bool
pre true.
post The returned value is true if the character c appears in the sequence s at least once, and is false if c does not appear at all in s.
(If s is the empty string, then it contains no characters, and ISIN (c, s) will be false whatever the character c is.)
Activity 20
Suggest a description for a function ISEMPTY corresponding to the following process.
Determine whether or not a given sequence is empty.
Discussion
The function will input a sequence (which might contain elements from any set, say X). It can return true if the sequence is empty, and false if it is not empty. So we can use the following description of ISEMPTY.
function ISEMPTY (s in SeqOfX ) return in Bool
pre true.
post The returned value is true if the sequence s contains no members, and is false if s contains one or more members.
Objectives for Section 4
After studying this section you should be able to do the following.
Recognise and use the terminology: function, signature, domain, semantics, input set, output set, precondition, postcondition.
Suggest appropriate signatures and preconditions for functions corresponding to a variety of processes on numbers, characters and sequences, including those with more than one input and those that return a Boolean value.
For given inputs, give the value returned by various functions described in this section, in particular: AT, PUT, SIZE, ASC, CHR, ADDLAST.
Exercises on Section 4
Exercise 9
For each of the following functions, give the signature and suggest a suitable precondition.
(a) TOUPPER, which changes a string, containing only lower-case letters, into the corresponding string consisting of upper-case letters. (So, for example, TOUPPER(“word”) = “WORD”.)
(b) REMOVELAST, which, given a sequence, deletes its last member.
(c) LAST, which returns the last member of a sequence.
Answer
Solution
(a) This function inputs a string and outputs a string, therefore it has signature TOUPPER : SeqOfChar → SeqOfChar. It requires a precondition that the input sequence consists entirely of lower-case letters.
(b) The members of the sequence may come from any set, which we will denote by X. The input is a sequence and the returned value is also a sequence. So the signature is REMOVELAST : SeqOfX → SeqOfX . The input sequence should contain at least one member (otherwise there is no last member to delete), so we need a precondition that the input sequence is not empty.
(c) This is similar to (a), except that the returned value is an item from X, rather than a sequence. The signature is LAST : SeqOfX → X. We again need the precondition that the input sequence is not empty.
Exercise 10
Suppose that the days of the week are represented by numbers, with Mon-day represented by 1, Tuesday represented by 2, and so on, with Sunday represented by 7. Describe a function TOMORROW2, giving the next day with Days represented in this way.
Answer
Solution
You may have given this description.
function TOMORROW2(d in Int) return in Int
pre d is in the set {1,2,3,4,5,6,7}.
post The returned value is t, where:
if d = 1 then t = 2
if d = 2 then t = 3
if d = 3 then t = 4
if d = 4 then t = 5
if d = 5 then t = 6
if d = 6 then t = 7
if d = 7 then t = 1.
Or you may have given a shorter description, such as:
function TOMORROW2(d in Int) return in Int
pre 1 ≤ d ≤ 7.
post The returned value is t, where:
t = d + 1 if 1 = d = 6;
t = 1 if d = 7.
Either of these answers is fine.
Exercise 11
(a) With s = “abcd”, evaluate each of:
(i) AT(1, s);
(ii) PUT(2, s, AT(1, s)).
(b) For a general sequence s, describe how the sequence PUT(2, s, AT(1, s)) is obtained from s.
The functions AT and PUT were described in Activity 16.
Answer
Solution
(a)(i) With s = “abcd”, AT(1,s) = ‘a’.
(ii) Then PUT(2,s,AT(1,s)) = PUT(2,“abcd”,‘a’) = “aacd”.
(b) In general, PUT(2,s,AT(1,s)) is formed by replacing the second member of the sequence s with a copy of the first member of s.
5 Operations and comparisons
Seeing processes as functions
Addition of numbers is a process that one would expect a computer to be able to perform. Now we write the result of adding the numbers 5 and 2 as 5 + 2, for example. The symbol +, which represents the process of addition, appears between the two numbers being added. This is known as infix notation. Infix notation may be used for processes that combine two data items of the same type. Addition, subtraction and multiplication of numbers are familiar examples. We also use infix notation when writing a comparison of the size of two numbers, such as 5
In this section, we shall show that a process such as addition of numbers is a function. Perhaps more surprisingly, a process such as
5.1 Arithmetic operations
Processes such as addition of numbers are called binary operations. (The word “binary” here reflects the fact that a binary operation combines two data items.) A binary operation is a particular form of function. To see this, we need to recognise the appropriate signature.
If you add two integers, then the resulting value is also an integer. So addition of integers takes two integers and returns an integer value. Thus adding integers is a function with signature Int × Int → Int. We can add any two integers, so addition is a total function (that is, has precondition true). We can describe a function, +, corresponding to addition of integers, as below.
function (infix) (x + y on Int) return in Int
pre true.
post The returned value is the result of adding x and y.
Where we use infix notation to write the value returned by a function, we will set out the signature line in the function description in a slightly different way from that used in Section 4, as illustrated above.
Activity 21
Describe a function, −, corresponding to integer subtraction written using infix notation.
Discussion
Subtraction again combines two integers to produce an integer value. We can subtract any two integers, so this is again a total function.
function (infix) (x − y on Int) return in Int
pre true.
post The returned value is the result of subtracting y from x.
We saw in Activity 3 that division of one integer by another does not necessarily result in an integer. For example, 2 ÷ 4 = 0.5 and 0.5 is not an integer. This means that we cannot define a function for what we might call “everyday division” that returns an integer value for integer inputs.
Sometimes, we need a form of division of integers that does yield an integer result. For example, suppose our supermarket features a special ‘buy 4, get 1 free’ order on bottles of wine. If a customer comes to the till with nine bottles of wine, then the till needs to calculate how many free bottles they should receive. Now nine bottles of wine contain two lots of four bottles (with one bottle left over). So the customer receives two free bottles of wine. This is an example of integer division. Integer division of 9 by 4 gives the result 2. (Hopefully, the cashier will point out to the customer with 9 bottles of wine that they are entitled to another free bottle!)
As another example, suppose that we want to perform integer division of 29 by 8. Now 3 × 8 = 24, while 4 × 8 = 32. When we perform integer division of 29 by 8 we obtain the result 3. Since 29 − 3 × 8 = 5, dividing 29 by 8 leaves a remainder of 5. Notice that the remainder, 5, satisfies the condition that 0 ≤ 5
Integer division has two integers as input. It is a binary operation on Int, so we could use infix notation to write integer division. Now, many programming languages use / as an infix notation for both integer division and for real number division. In such cases, it is vital to appreciate that these are different processes, whose precise behaviour depends upon the type of the values supplied. To emphasise that integer division is not the familiar process of “everyday division”, we will write it as DIV, and use function rather than infix notation to give its values. For example, DIV (29, 8) = 3.
How can we describe integer division in general? To do this, some vocabulary is useful. In writing DIV (29, 8) = 3, the number 8 is called the divisor, and 3 is called the quotient.
We can generalise the equation 29 = 3 × 8 + 5 to give n = q × d + r (where d is the divisor, q is the quotient and r the remainder). The remainder must not be too large. In this example, the remainder 5 is less than 8. In general, the remainder r must be less than the divisor, d. Also, the remainder r is not negative. We can express these conditions on r algebraically as 0 ≤ r d. So, in general, the quotient, q, is the largest integer by which we can multiply the divisor, d, while leaving a remainder that is not negative. If we subtract (q × d) from n, the resulting remainder needs to be non-negative and less than d.
Integer division has two integers as inputs and returns an integer. So the integer division function has signature DIV : Int × Int → Int. Since we write DIV using function notation, we can describe this function as below.
function DIV (n in Int, d in Int) return in Int
pre d > 0.
post The returned value q is the result of integer division of n by d. It satisfies the condition that if r = n − (q × d), then we have 0 ≤ r d.
Notice that we only consider the case where the divisor, d, is strictly greater than 0. There is no restriction on the number n that is being divided, though. The examples we have considered so far have n positive.
What do these semantics give if n n = −29 and d = 8. We have −29 = −4 × 8 + 3 and the semantics give DIV (−29, 8) = −4. (Note that the remainder, r = 3, satisfies the condition 0 ≤ r d, which is 0 ≤ r
If n = 0, we have DIV (0, d) = 0 for any d that satisfies the precondition.
Activity 22
Give the following values:
(a) DIV (27,4).
(b) DIV (32,17).
(c) DIV (−27, 4).
(d) DIV (0,6).
(e) DIV (3,0).
Discussion
(a) DIV (27,4) = 6, since 27 = 6 × 4 + 3, where 0 ≤ 3
(b) DIV (32,17) = 1, since 32 = 1 × 17 + 15, where 0 ≤ 15
(c) DIV (−27, 4) = −7, since −27 = −7 × 4 + 1, where 0 ≤ 1
(d) DIV (0,6) = 0.
(e) This is undefined (because of the precondition on DIV ).
A second process associated with integer division returns the remainder rather than the quotient. This is again a binary operation. We will write this operation as MOD(n, d). This operation can be described as below.
function MOD(n in Int, d in Int) return in Int
pre d > 0.
post The returned value r is the remainder after integer division of n by d. It satisfies the conditions 0 ≤ r d and r = n - (q × d), where q is an integer. The remainder MOD(n, d) is sometimes called the value of n modulo d, or more briefly n mod d. Many programming languages use the infix notation n % d for this operation.
Activity 23
Give the following values:
(a) MOD(67, 10).
(b) MOD(55, 5).
(c) MOD(−27, 4).
Discussion
(a) MOD(67, 10) = 7 (since 67 = 6 × 10 + 7; the remainder on division of 67 by 10 is 7).
(b) MOD(55, 5) = 0 (since 55 = 11 × 5 + 0).
(c) MOD(−27, 4) = 1 because, as noted in Activity 22(c), we have −27 = −7 × 4 + 1.
Activity 24
(a) Suppose that you buy 335 grams of walnuts at 299 pence per kg, and the price of this purchase is expressed as a whole number of pence by ignoring any fraction. What is the cost of this purchase?
(b) Now consider a general purchase of this form, of weight grams of a product costing price pence per kilogram. Using the function DIV , give a formula for the cost of such a purchase.
Discussion
(a) 335 grams is 0.335 kilograms, so this purchase should cost 0.335 × 299 = 100.464 pence, which will be rounded to 100 pence. (Reassuringly, this is the same as the cost given in Figure 2.)
(b) In general we multiply weight and price, and divide the result by 1000, ignoring any fractional part of the result. So the required value is given by the expression DIV (weight × price,1000).
5.2 Operations on Boolean values
The idea of a binary operation, and the use of infix notation, is not confined to numbers. Infix notation may be used for any process with two inputs from the same set. We look now at two binary operations on Boolean values that are often used.
The first of these takes two Boolean values, and returns true if both of the input values are true and returns false otherwise. It is a binary operation, and we shall write it using the infix notation ∧, where the symbol ∧ can be read as “and”. So a ∧ b is true only when a and b are both true. We can describe the function corresponding to this operation as below (The operation ∧ is also known as conjunction).
function (infix) (a ∧ b on Bool) return in Bool
pre true.
post The returned value is true if both a = true and b = true, and is false otherwise.
Alternatively, we could give the semantics of ∧ by listing the returned value in each of four cases, giving the four possible combinations of input values. Using this approach, we could express the postcondition as follows.
post The returned value is c, where
if a = true and b = true then c = true
if a = true and b = false then c = false
if a = false and b = true then c = false
if a = false and b = false then c = false.
A second binary operation on Boolean values returns true if either (or both) of the two Boolean values is true. We write this operation using the infix symbol ∨ , where ∧ can be read as “or”. The corresponding function is described below. The operation ∨ is also known as disjunction.
function (infix) (a ∨ b on Bool) return in Bool
pre true.
post The returned value is false if both a = false and b = false, and is true otherwise.
Activity 25
Give the semantics of ∨ by listing the returned value in each of four cases, giving the four possible combinations of input values.
Discussion
We can express the postcondition in the description above as follows.
post The returned value is c, where
if a = true and b = true then c = true
if a = true and b = false then c = true
if a = false and b = true then c = true
if a = false and b = false then c = false.
Another useful process on Boolean values inputs a single Boolean value, and returns the reverse of that value. This process, called negation, is not a binary operation, since it has one input only. We call this function NOT, and we have
NOT(false) = true, and NOT(true) = false.
Activity 26
(a) Give a full description of the function NOT.
(b) If a = true and b = false, evaluate each of:
(i) a ∨ b;
(ii) NOT(a ∨ b);
(iii) a ∧ (a ∨ b).
Discussion
(a) A description is given below.
function NOT(a in Bool) return in Bool
pre true.
post The returned value is false if a = true and is true if a = false.
(b) (i) Substituting for a and b, we have true ∨ false = true.
(ii) We should evaluate the term in brackets first: true ∨ false = true. Then NOT(true) = false. So NOT(a ∨ b) = false.
(iii) Again, evaluate the term in brackets first: (true ∨ false) = true. Then the given expression becomes true ∧ true which evaluates to true.
5.3 Comparison functions
Another situation where we use infix notation is in writing comparisons, such as x , where x and y are numbers. Such a comparison is either true or false. For example, 5 Bool = {true, false}. Thus the comparison
function (infix) (x on Int) return in Bool
pre true.
post The returned value is true if x y and is false otherwise.
Equality is also a comparison function. This is normally written using the infix symbol =. If x and y are numbers, then x = y is true if the numbers x and y are the same and is false if they are not. If one is working with real numbers on a computer, then one needs to be very careful with tests of equality. There will be an element of approximation in the way real numbers are stored, and this may result in a computer reporting real numbers as equal when they are only approximately equal. However, we shall confine our attention to integers, where there is no such problem in deciding whether two numbers are the same.
Sometimes we may wish to test to see whether two characters are the same. (This can be done by comparing their ASCII codes, for example.) A computer will need to work in a different way when comparing two integers for equality from that needed when comparing two characters for equality. These are different processes. Equality of numbers is a function with signature Int × Int → Bool; equality of characters, on the other hand, has signature Char × Char → Bool. Since these are different functions, we will give them different identifiers. We will write =Int for equality of integers and =Char for equality of characters.
function (infix) (x =Int y on Int) return in Bool
pre true.
post The returned value is true if the integers x and y are equal and is false otherwise.
function (infix) (x =Char y on Char) return in Bool
pre true.
post The returned value is true if the characters x and y are the same and is false otherwise.
One could give a binary operation Int in the identifier Int for comparison of integers above).
Note that in mathematics the term binary operation would only be used for a total function whose return type is the same as the type of the inputs.
Activity 27
Give a full description of an infix function corresponding to Char comparing two characters by comparing their ASCII codes.
Discussion
A description is given below.
function (infix) (x Char y on Char) return in Bool
pre true.
post The returned value is true if ASC(x) Int ASC (y) and is false otherwise.
In practice, a variety of different comparisons are used on integers (and other forms of data, such as characters), including: > (strictly greater than), ≤ (less than or equal), ≥ (greater then or equal), and ≠ (not equal). Functions may be described for each of these, but we shall not do so here.
5.4 Expressions
In computer code, one may want to formulate an expression to achieve some particular purpose, such as to express some condition about the states of variables involved in the code. For example, suppose that you want to express the condition that a sequence s contains at least two members, and that the second member of s is not the space character (with ASCII code 32). This condition holds when the expression below is true.
(SIZE(s) > Int 1) ∧ (NOT(ASC(AT(2,s)) = Int 32))
When writing expressions involving functions and binary operations, there are some points to be careful about. One needs to be careful to use brackets as necessary to ensure that operations are applied in the desired order. This is particularly important in expressions using infix notation. You also need to apply each process in a way that is consistent with its signature. And you must apply each process in a way that is consistent with any precondition that it has. We say that an expression is not valid if it uses a function in a way that is inconsistent with its signature or its precondition. For example, ‘Q’ =Int 32 is not valid, since =Int compares two integers, and ‘Q’ is a character, while PUT(7, “This”, ‘Q’) is not valid, since 7 does not satisfy the precondition of PUT. (The precondition of PUT requires that 7≤ SIZE(“This”), but SIZE(“This”) is 4.)
The functions SIZE and AT were described in Activity 16, and the function ASC was described in Section 4.3. The binary operations =Int , >Int and ∧ are defined earlier in this section.
Activity 28
(a) With s = “I#am.”, evaluate each of the expressions:
(i) AT(2, s).
(ii) ASC(AT(2, s)).
(iii) ASC(AT(2, s)) =Int 35.
(iv) NOT(ASC(AT(2, s)) =Int 35).
(v) (SIZE(s) >Int 3) ∧ (NOT (ASC (AT (2, s)) =Int 35)).
(b) Let s be a general string. Under what circumstances does the expression in (a) (v) give the value true? Under what circumstances is that expression valid?
(c) With s = “I#am.”, why is it not possible to evaluate the expression
(ASC(AT(2,s)) = Int 35)?
Discussion
(a) (i) AT(2, s) = ‘#’.
(ii) ASC(AT(2, s)) = 35.
(iii) ASC(AT(2, s)) =Int 35 becomes 35 =Int 35, which evaluates to true.
(iv) NOT(ASC(AT(2, s)) =Int 35) becomes NOT (true) = false.
(v) We have SIZE(s) = 5 (the number of characters in the string “I#am.”), so (SIZE(s) >Int 3) becomes (5 >Int 3) which is true. So the expression in (v) becomes true ∧ false = false.
(b) The given expression will be true only if each of SIZE(s) >Int 3 and NOT(ASC(AT(2, s)) =Int 35) is true. The first of these is true if the string s contains at least four characters. The second is true if the second character is s is not the character ‘#’. So the expression in (a) (v) will be true if:
the string s contains at least four characters and its second character is not ‘#’.
The precondition of AT requires here that the string s contains at least two characters. The expression in (a) (v) will be valid so long as this is true. (All the other functions in the expression are total. The example in part (a) indicates that the expression is put together in a way that is consistent with the signatures of the functions.)
(c) AT(2,s) = ‘#’. Then AT(2,s) =Int 35 becomes ‘#’ =Int 35. This expression is not valid, since =Int requires two integers as inputs, and ‘#’ is a character. So the given expression is not valid.
Notice how important the brackets are in a complicated expression. The order in which the bits of the overall expression are to be evaluated is determined by the way the brackets appear in the expression. We need to follow this carefully in evaluating an expression such as that in Activity 28 (a) (v). A slip in placing one bracket can easily lead to an expression that is not valid, as in (c) above. On the whole, it is good practice when writing computing code to seek to avoid writing complicated expressions. Usually one can split the code into intermediate steps, as indicated by the steps in the evaluation in (a) above.
Objectives for Section 5
After studying this section you should be able to do the following.
Recognise and use the terminology: binary operation, infix notation, quotient and remainder (associated with integer division).
Use the notation for various binary operations introduced in the text, in particular DIV and MOD on integers; and ∧ (and) and ∨ (or) on Boolean values.
Suggest appropriate signatures and preconditions for functions corresponding to binary operations, including comparisons that return Boolean values.
Evaluate expressions involving functions and binary operations introduced in the text. Take note of where brackets appear in an expression.
Recognise an expression that is invalid because it uses a process in a way inconsistent with its signature or precondition.
Exercises on Section 5
Exercise 12
Give a full description of a function (using the infix notation ×) corresponding to multiplication of integers.
Answer
Solution
A suitable description of integer multiplication is given below.
function (infix) (x × y on Int) return in Int
pre true.
post The returned value is the result of multiplying x and y.
Exercise 13
With n = 966, evaluate each of:
(a) MOD(n, 10);
(b) DIV (n, 10);
(c) MOD(DIV (n, 10), 10).
Answer
Solution
966 = 96 × 10 + 6. So (a) MOD(966, 10) = 6 (the remainder when 966 is divided by 10), and (b) DIV (966,10) = 96. Then (c) MOD(DIV (966, 10), 10) becomes MOD(96, 10). This evaluates to 6, which is the remainder when 96 is divided by 10.
Exercise 14
The function LAST is described below.
function LAST(s in SeqOfX ) return in X
pre s is not empty.
post The returned value is the last element in s. For example, LAST([1, 2, 3]) = 3.
Consider the expression NOT(LAST(s) =Char LAST (t)).
(a) What is the value of this expression if s is “the” and t is:
(i) “same”;
(ii) “different”?
(b) Under what circumstances does this expression have the value true?
(c) Is this expression valid with s = [1,2] and t = [1,8,4,2]?
Answer
Solution
(a) If s = “the” then LAST(s) = ‘e’. (i) With t = “same”, we have LAST(t) = ‘e’, and the given expression becomes
NOT(‘e’ =Char ‘e’) = NOT (true) = false.
(i) With t = “different”, we have LAST(t) = ‘t’, and the given expression becomes
NOT(‘e’ =Char ‘t’) = NOT (false) = true.
(b) The given expression is true if the strings s and t have different last letters.
(c) With these values of s and t, the given expression becomes NOT(2 =Char 2). Now =Char compares two characters, and 2 is an integer. So this expression is not valid. (For the given expression to be valid, we need s and t to be sequences of characters, and to be non-empty, so that the precondition of LAST is satisfied.)
Conclusion
We discussed forms of data and processes relevant to an electronic till in a supermarket. In particular, we introduced the idea of a sequence of data items.
A number of fundamental forms of data were introduced. We distinguished two types of number: integers (positive or negative whole numbers, or 0), and real numbers (thought of as decimal numbers and approximated in computers as floating point numbers). Characters may be thought of as symbols that may be entered from a computer keyboard by a single keystroke. Each character is associated with an integer code and we introduced one such encoding called the ASCII code. The Boolean values true and false form another fundamental form of data.
Data may be structured in a collection. Different forms of collection are possible. We looked at two: sets and sequences. In a sequence, the order in which the items appear in the collection is important and an item may appear more than once. In a set, one is only interested in the different items appearing in the collection, and the order in which these items are listed is of no significance, nor is repetition of an item.
The Cartesian product of sets X and Y is written X × Y , and is the set consisting of all ordered pairs (x, y), where x is in X and y is in Y . An ordered pair is also called a 2-tuple. More generally, an n-tuple is an association of n items, each taken from a specified set. An n-tuple is written in round brackets, and is a member of a Cartesian product set combining n component sets. For example, a member of the set Int × Char × Int × SeqOfChar would be a 4-tuple, such as (121, ‘y’, 6, “Qwerty”).
The disjoint union of sets X and Y, written X
 Y, consists of all items that come either from X or from Y (where X and Y have nothing in common). This is useful when we want to mix different forms of data in a sequence.
Y, consists of all items that come either from X or from Y (where X and Y have nothing in common). This is useful when we want to mix different forms of data in a sequence.A function is a process that returns a unique value for each permitted input. To give a full description of a function, we give: its signature (name, and input and output sets), a precondition (which may be true), and a postcondition giving its semantics. The semantics should be an unambiguous statement of the relationship between the returned value and the input(s).
If a function has more than one input, then its input set will be a Cartesian product. If a function returns a value that is true or false, then the output set will be Bool. Usually, the semantics of a function are given by a general rule, or possibly by a formula. However, in some cases we need to list the returned value for each possible input. For example, this would be the case for a function returning the price of each barcoded product stocked by a supermarket.
A binary operation is a process, such as addition of integers, that inputs two data items of the same type. A binary operation can be written using infix notation (as in x + y, for example). Addition of integers corresponds to a function with signature Int × Int → Int. We described integer division. Integer division of n by d returns an integer, written DIV (n, d). It also leaves a remainder, denoted by MOD(n, d).
We noted that binary operations are not confined to those on numbers. We described two binary operations on Boolean values that are frequently useful: ∨ (read as “or”) and ∧ (read as “and”). We also introduced the function NOT on Booleans.
Comparisons, such as Bool. For example, =Char , a test of whether two characters are identical, corresponds to a function with signature Char × Char → Bool.
Acknowledgements
Except for third party materials and otherwise stated (see terms and conditions), this content is made available under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Licence
Course image: Creativity103 in Flickr made available under Creative Commons Attribution 2.0 Licence.
All materials included in this course are derived from content originated at the Open University.
Don't miss out:
If reading this text has inspired you to learn more, you may be interested in joining the millions of people who discover our free learning resources and qualifications by visiting The Open University - www.open.edu/ openlearn/ free-courses
Copyright © 2016 The Open University