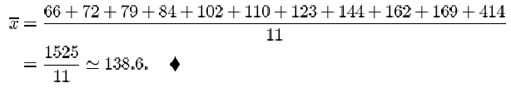Exploring data: graphs and numerical summaries
Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Friday, 19 April 2024, 11:44 PM
Exploring data: graphs and numerical summaries
Introduction
This course will introduce you to a number of ways of representing data graphically and of summarising data numerically. You will learn the uses for pie charts, bar charts, histograms and scatterplots. You will also be introduced to various ways of summarising data and methods for assessing location and dispersion.
This OpenLearn course is an adapted extract from the Open University course M248 Analysing data.
Learning outcomes
After studying this course, you should be able to:
understand and use standard symbols and notation: for the pth value in a data set when the values are written in order, the sample lower and upper quartiles and the sample median, the sample mean and the standard deviation
understand that data can have a pattern which may be represented graphically
understand that the standard deviation and the interquartile range are measures of the dispersion in a data set
understand that the median and the interquartile range are more resistant measures than are the mean and the standard deviation
identify an overall 'feel' for data and the way it is distributed by constructing appropriate graphical displays.
1 Introducing data
Chambers English Dictionary defines the word data as follows.
data, dātä,, n.pl. facts given, from which others may be inferred:—sing. da'tum(q.v.) …. [L. data, things given, pa.p. neut. pl. of dare, to give.]
You might prefer the definition given in the Shorter Oxford English Dictionary.
data, things given or granted; something known or assumed as fact, and made the basis of reasoning or calculation.
Data arise in many spheres of human activity and in all sorts of different contexts in the natural world about us. Statistics may be described as exploring, analysing and summarising data; designing or choosing appropriate ways of collecting data and extracting information from them; and communicating that information. Statistics also involves constructing and testing models for describing chance phenomena. These models can be used as a basis for making inferences and drawing conclusions and, finally, perhaps for making decisions. The data themselves may arise in the natural course of things (for example, as meteorological records) or, commonly, they may be collected by survey or experiment.
In this course we begin by examining several different data sets and describing some of their features.
Data are frequently expressed as nothing more than a list of numbers or a complicated table. As a result, very large data sets can be difficult to appreciate and interpret without some form of consolidation. This can, perhaps, be achieved via a series of simpler tables or an easily assimilated diagram. The same applies to smaller data sets, whose main message may become evident only after some procedure of sorting and summarising.
Before computers were widely available, it was often necessary to make quite detailed theoretical assumptions before beginning to investigate the data. But nowadays it is relatively easy to use a statistical computer package to explore data and acquire some intuitive ‘feel’ for them, without making such assumptions. This is helpful in that the most important and informative place to start is the logical one, namely with the data themselves. The computer will make your task both possible and relatively quick.
However, you must take care not to be misled into thinking that computers have made statistical theory redundant: this is far from the truth. You will find the computer can only lead you to see where theory is needed to underpin a commonsense approach or, perhaps, to reach an informed decision. It cannot replace such theory and it is, of course, incapable of informed reasoning: as always, that is up to you. Even so, if you are to gain real understanding and expertise, your first steps are best directed towards learning to use your computer to explore data, and to obtain some tentative inferences from such exploration.
The technology explosion of recent years has made relatively cheap and powerful computers available to all of us. Furthermore, it has brought about an information explosion which has revolutionised our whole environment. Information pours in from the media, advertisements, government agencies and a host of other sources and, in order to survive, we must learn to make rational choices based on some kind of summary and analysis of it. We need to learn to select the relevant and discard the irrelevant, to sift out what is interesting, to have some kind of appreciation of the accuracy and reliability of both our information and our conclusions, and to produce succinct summaries which can be interpreted clearly and quickly.
Our methods for summarising data will involve producing graphical displays as well as numerical calculations. You will see how a preliminary pictorial analysis of your data can, and indeed should, influence your entire approach to choosing a valid, reliable method.
But we shall begin, in Section 1 of this course, with the data themselves. In this course, except where it is necessary to make a particular theoretical point, all of the data sets used are genuine; none are artificial, contrived or ‘adjusted’ in any way. In Section 1 you will encounter several sets of real data, and begin to look at some questions on which they can throw light.
Statistics exists as an academic and intellectual discipline precisely because real investigations need to be carried out. Simple questions, and difficult ones, about matters which affect our lives need to be answered, information needs to be processed and decisions need to be made. ‘Finding things out’ is fun: this is the challenge of real data.
Some basic graphical methods that can be used to present data and make clearer the patterns in sets of numbers are introduced in Sections 2 and 3: pie charts and bar charts in Section 2, histograms and scatterplots in Section 4.
Finally, in Section 4 we discuss ways of producing numerical summaries of certain aspects of data sets, including measures of location (which are, in a sense, ‘averages’), measures of the dispersion or variability of a set of data, and measures of symmetry (and lack of symmetry).
2 Data and questions
The data sets you will meet in this section are very different from each other, both in structure and character. By the time you reach the end of the course, you will have carried out a preliminary investigation of each, identified important questions about them and made a good deal of progress with some of the answers. As you work through the course developing statistical expertise, several of these data sets will be revisited and different questions addressed.
There are seven data sets here. You do not need to study them in great detail at this early stage. You should spend just long enough to see how they are presented and to think about the questions that arise. We shall be looking at all of them in greater detail as this course proceeds. However, if you think you have identified something interesting or unusual about any one of them, make a note of your idea for later in the course.
2.1 Nuclear power stations
The first data set is a very simple one. Table 1 shows the number of nuclear power stations in various countries throughout the world before the end of the cold war (that is, prior to 1989). The names of the countries listed are those that pertained at the time the data were collected.
| Country | Number |
|---|---|
| Canada | 22 |
| Czechoslovakia | 13 |
| East Germany | 10 |
| France | 52 |
| Japan | 43 |
| South Korea | 9 |
| Soviet Union | 73 |
| Spain | 10 |
| Sweden | 12 |
| UK | 41 |
| USA | 119 |
| West Germany | 23 |
You could scarcely have a more straightforward table than this, and yet it is by no means clear what is the most meaningful and appealing way to show the information.
2.2 USA workforce
The data set in Table 2 comprises the figures published by the US Labor Department for the composition of its workforce in 1986. It shows the average numbers over the year of male and female workers in the various different employment categories and is typical of the kind of data published by government departments.
| Type of employment | Male (millions) | Female (millions) |
|---|---|---|
| Professional | 15.00 | 11.60 |
| Industrial | 12.90 | 4.45 |
| Craftsmen | 12.30 | 1.25 |
| Sales | 6.90 | 6.45 |
| Service | 5.80 | 9.60 |
| Clerical | 3.50 | 14.30 |
| Agricultural | 2.90 | 0.65 |
In spite of this being a small and fairly straightforward data set, it is not easy to develop an intuitive ‘feel’ for the numbers and their relationships with each other when they are displayed as a table.
Activity 1: USA workforce
Given the USA workforce data, what questions might you ask?
Discussion
One question is: what is the most meaningful and appealing way to show the information? You might want to decide how best you can compare the male and female workforces in each category. It is possible that the most important question involves comparisons between the total number of employees in each of the seven categories.
2.3 Infants with SIRDS
The data in Table 3 are the recorded birth weights of 50 infants who displayed severe idiopathic respiratory distress syndrome (SIRDS). This is a serious condition which can result in death.
| 1.050* | 2.500* | 1.890* | 1.760 | 2.830 |
| 1.175* | 1.030* | 1.940* | 1.930 | 1.410 |
| 1.230* | 1.100* | 2.200* | 2.015 | 1.715 |
| 1.310* | 1.185* | 2.270* | 2.090 | 1.720 |
| 1.500* | 1.225* | 2.440* | 2.600 | 2.040 |
| 1.600* | 1.262* | 2.560* | 2.700 | 2.200 |
| 1.720* | 1.295* | 2.730* | 2.950 | 2.400 |
| 1.750* | 1.300* | 1.130 | 3.160 | 2.550 |
| 1.770* | 1.550* | 1.575 | 3.400 | 2.570 |
| 2.275* | 1.820* | 1.680 | 3.640 | 3.005 |
| *child died | ||||
(van Vliet, P.K. and Gupta, J.M. (1973) Sodium bicarbonate in idiopathic respiratory distress syndrome. Arch. Disease in Childhood, 48, 249–255.)
At first glance, there seems little that one can deduce from these data. The babies vary in weight between 1.03 kg and 3.64 kg. Notice, however, that some of the children died. Surely the important question concerns early identification of children displaying SIRDS who are at risk of dying. Do the children split into two identifiable groups? Is it possible to relate the chances of survival to birth weight?
2.4 Runners
The next data set relates to 22 of the competitors in an annual championship run, the Tyneside Great North Run. Blood samples were taken from eleven runners before and after the run, and also from another eleven runners who collapsed near the end of the race. The measurements are plasma β endorphin concentrations in pmol/litre. The letter β is the Greek lower-case letter beta, pronounced ‘beeta’. Unless you have had medical training you are unlikely to know precisely what constitutes a plasma β endorphin concentration, much less what the units of measurement mean. This is a common experience even among expert statisticians working with data from specialist experiments, and can usually be dealt with. What matters is that some physical attribute can be measured, and the measurement value is important to the experimenter. The statistician is prepared to accept that running may have an effect upon the blood, and will ask for clarification of medical questions as and when the need arises. The data are given in Table 4.
| Normal runner before race | Same runner after race | Collapsed runner after race |
|---|---|---|
| 4.3 | 29.6 | 66 |
| 4.6 | 25.1 | 72 |
| 5.2 | 15.5 | 79 |
| 5.2 | 29.6 | 84 |
| 6.6 | 24.1 | 102 |
| 7.2 | 37.8 | 110 |
| 8.4 | 20.2 | 123 |
| 9.0 | 21.9 | 144 |
| 10.4 | 14.2 | 162 |
| 14.0 | 34.6 | 169 |
| 17.8 | 46.2 | 414 |
(Dale, G., Fleetwood, J.A., Weddell, A., Ellis, R.D. and Sainsbury, J.R.C. (1987) Beta-endorphin: a factor in ‘fun run’ collapse? British Medical Journal 294, 1004.)
You can see immediately that there is a difference in β endorphin concentration before and after the race, and you do not need to be a statistician to see that collapsed runners have very high β endorphin concentrations compared with those who finished the race. But what is the relationship between initial and final β endorphin concentrations? What is a typical finishing concentration? What is a typical concentration for a collapsed runner? How do the sets of data values compare in terms of how widely they are dispersed around a typical value?
The table raises other questions. The eleven normal runners (in the first two columns) have been sorted according to increasing pre-race endorphin levels. This may or may not help make any differences in the post-race levels more immediately evident. Is this kind of initial sorting necessary, or even common, in statistical practice? The data on the collapsed runners have also been sorted. The neat table design relies in part on the fact that there were eleven collapsed runners measured, just as there were eleven finishers, but the two groups are independent of each other. There does not seem to be any particularly obvious reason why the numbers in the two groups should not have been different. Is it necessary to the statistical design of this experiment that the numbers should have been the same?
2.5 Cirrhosis and alcoholism
The data in Table 5, which are given for several countries in Europe and elsewhere, are the average annual alcohol consumption in litres per person and the death rate per 100 000 of the population from cirrhosis and alcoholism. It would seem obvious that the two are related to each other, but what is the relationship and is it a strong one? How can the strength of such a relationship be measured? Is it possible to assess the effect on alcohol-related deaths of taxes on alcohol, or of laws that aim to reduce the national alcohol consumption?
| Country | Annual alcohol consumption (1/person) | Cirrhosis & alcoholism (death rate/100 000) |
|---|---|---|
| France | 24.7 | 46.1 |
| Italy | 15.2 | 23.6 |
| W. Germany | 12.3 | 23.7 |
| Austria | 10.9 | 7.0 |
| Belgium | 10.8 | 12.3 |
| USA | 9.9 | 14.2 |
| Canada | 8.3 | 7.4 |
| England & Wales | 7.2 | 3.0 |
| Sweden | 6.6 | 7.2 |
| Japan | 5.8 | 10.6 |
| Netherlands | 5.7 | 3.7 |
| Ireland | 5.6 | 3.4 |
| Norway | 4.2 | 4.3 |
| Finland | 3.9 | 3.6 |
| Israel | 3.1 | 5.4 |
(Osborn, J.F. (1979) Statistical exercises in medical research. Blackwell Scientific Publications, Oxford, p.44.)
France has a noticeably higher average annual individual alcohol consumption than the others; the figure is more than double that of third-placed West Germany. The French alcohol-related death rate is just under double that of the next highest.
Activity 2: Alcohol consumption and death rate
Bearing in mind the comments above, summarise the information you might wish to glean from these data. Have you any suggestions for displaying the data?
Discussion
You would wish to know whether the death rate is directly related to alcohol consumption and, if so, how. You would also need to know if the figures for France should be regarded as atypical. If so, how should they be handled when the data are analysed?
One suggestion for displaying the data would be to plot a graph of death rate against alcohol consumption.
2.6 Body weights and brain weights for animals
The next data set comprises average body and brain weights for 28 kinds of animal, some of them extinct. The data are given in Table 6.
| Species | Body weight (kg) | Brain weight (g) |
|---|---|---|
| Mountain Beaver | 1.350 | 8.100 |
| Cow | 465.000 | 423.000 |
| Grey Wolf | 36.330 | 119.500 |
| Goat | 27.660 | 115.000 |
| Guinea Pig | 1.040 | 5.500 |
| Diplodocus | 11700.000 | 50.000 |
| Asian Elephant | 2547.000 | 4603.000 |
| Donkey | 187.100 | 419.000 |
| Horse | 521.000 | 655.000 |
| Potar Monkey | 10.000 | 115.000 |
| Cat | 3.300 | 25.600 |
| Giraffe | 529.000 | 680.000 |
| Gorilla | 207.000 | 406.000 |
| Human | 62.000 | 1320.000 |
| African Elephant | 6654.000 | 5712.000 |
| Triceratops | 9400.000 | 70.000 |
| Rhesus Monkey | 6.800 | 179.000 |
| Kangaroo | 35.000 | 56.000 |
| Hamster | 0.120 | 1.000 |
| Mouse | 0.023 | 0.400 |
| Rabbit | 2.500 | 12.100 |
| Sheep | 55.500 | 175.000 |
| Jaguar | 100.000 | 157.000 |
| Chimpanzee | 52.160 | 440.000 |
| Brachiosaurus | 87000.000 | 154.500 |
| Rat | 0.280 | 1.900 |
| Mole | 0.122 | 3.000 |
| Pig | 192.000 | 180.000 |
(Jerison, H.J. (1973) Evolution the brain and intelligence. Academic Press, New York.)
These data raise interesting questions about their collection and the use of the word ‘average’. Presumably some estimates may be based on very small samples, while others may be more precise. On what sampling experiment are the figures for Diplodocus, Triceratops and other extinct animals based? The three-decimal-place ‘accuracy’ given throughout the table here is extraordinary (and certainly needs justification).
Putting these concerns to one side for the moment, it would seem obvious that the two variables, body weight and brain weight, are linked. But what is the relationship between them and how strong is it? Can the strength of the relationship be measured? Is a larger brain really required to govern a larger body? These data give rise to a common problem in data analysis which experienced practical analysts would notice as soon as they look at such data. Can you identify the difficulty? Later, when we plot these data, you will see it immediately.
2.7 Surgical removal of tattoos
The final data set in this section is different from the others in that the data are not numerical. So far you have only seen numerical data in the form of measurements or counts. However, there is no reason why data should not be verbal or textual. Table 7 contains clinical data from 55 patients who have had forearm tattoos removed. Two different surgical methods were used; these are denoted by A and B in the table. The tattoos were of large, medium or small size, either deep or at moderate depth. The final result is scored from 1 to 4, where 1 represents a poor removal and 4 represents an excellent result. The gender of the patient is also shown.
| Method | Gender | Size | Depth | Score | Method | Gender | Size | Depth | Score | |
|---|---|---|---|---|---|---|---|---|---|---|
| A | M | Large | deep | 1 | B | M | medium | moderate | 2 | |
| A | M | Large | moderate | 1 | B | M | large | moderate | 1 | |
| B | F | Small | deep | 1 | A | M | medium | deep | 2 | |
| B | M | Small | moderate | 4 | B | M | large | deep | 3 | |
| B | F | Large | deep | 3 | A | F | large | moderate | 1 | |
| B | M | Medium | moderate | 4 | B | F | medium | deep | 2 | |
| B | M | Medium | deep | 4 | A | F | medium | deep | 1 | |
| A | M | Large | deep | 1 | A | M | medium | moderate | 3 | |
| A | M | Large | moderate | 4 | B | M | large | moderate | 3 | |
| A | M | Small | moderate | 4 | A | M | medium | deep | 1 | |
| A | M | Large | deep | 1 | A | F | small | deep | 2 | |
| A | M | Large | moderate | 4 | A | M | large | moderate | 2 | |
| A | F | Small | moderate | 3 | B | M | large | deep | 2 | |
| B | M | Large | deep | 3 | B | M | medium | moderate | 4 | |
| B | M | Large | deep | 2 | B | M | medium | deep | 1 | |
| B | F | Medium | moderate | 2 | B | F | medium | moderate | 3 | |
| B | M | Large | deep | 1 | B | M | large | moderate | 2 | |
| B | F | Medium | deep | 1 | B | M | large | moderate | 2 | |
| B | F | Small | moderate | 3 | B | M | large | moderate | 4 | |
| A | F | Small | moderate | 4 | B | M | small | deep | 4 | |
| B | M | Large | deep | 2 | B | M | large | moderate | 3 | |
| A | M | Medium | moderate | 4 | B | M | large | deep | 2 | |
| B | M | Large | deep | 4 | B | M | large | deep | 3 | |
| B | M | Large | moderate | 4 | A | M | large | moderate | 4 | |
| A | M | Large | deep | 4 | A | M | large | deep | 2 | |
| B | M | Medium | moderate | 3 | B | M | medium | deep | 1 | |
| A | M | Large | deep | 1 | A | M | small | deep | 2 | |
| B | M | Large | moderate | 4 |
(Lunn, A.D. and McNeil, D.R. (1988) The SPIDA manual. Statistical Computing Laboratory, Sydney.)
What are the relative merits of the two methods of tattoo removal? Is one method simply better, or does the quality of the result depend upon the size or depth of the tattoo?
2.8 Data and questions: summary
In this section you have met some real data sets and briefly considered some of the questions you might ask of them. They will be referred to and investigated in the remaining sections of this course. Some general principles that govern the efficacy and quality of data summaries and displays will be formulated. As you will discover, the main requirements of any good statistical summary/display are that it is informative, easy to construct, visually appealing and readily assimilated by a non-expert.
3 Pie charts and bar charts
The data set in Table 7 (section 1.8) comprised non-numerical or categorical data. Such data often appear in newspaper reports and are usually represented as one or other of two types of graphical display, one type is called a pie chart and the other a bar chart; these are arguably the graphical displays most familiar to the general public, and are certainly ones that you will have seen before. Pie charts are discussed in section 2.2 and bar charts in section 2.4. Some problems that can arise when using graphics of these types are discussed briefly in section 2.6.
3.1 Pie charts: surgical removal of tattoos
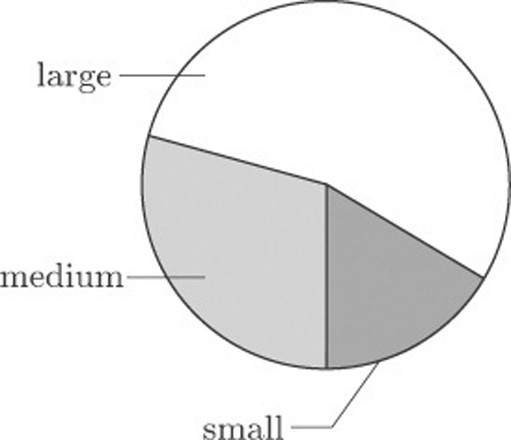
Suppose we count the numbers of large, medium and small tattoos from the data in Table 7: there were 30 large tattoos, 16 of medium size and 9 small tattoos. These data are represented in Figure 1. This display is called a pie chart.
This is an easy display to construct because the size of each ‘slice’ is proportional to the angle it subtends at the centre, which in turn is proportional to the count in each category. So, to construct Figure 1, you simply draw a circle and draw in radii making angles that represent the counts of large, medium and small tattoos respectively. For example, you can calculate the angle that represents the number of large tattoos as follows.
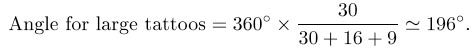
Activity 3: Tattoo sizes
Calculate the angles that represent the numbers of medium and small tattoos.
Answer
Solution
The angle for medium tattoos is
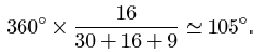
The angle for small tattoos is
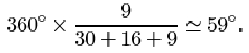
Once you have calculated the angles, you draw in the three radii that subtend them, and then shade the three sectors in order to distinguish them from each other.
At first sight the pie chart seems to fulfil the basic requirements of a good statistical display: it appears to be informative, easy to construct, visually appealing and readily assimilated by a non-expert.
Pie charts can be useful when all you want the reader to notice is that there were more large than medium size tattoos, and more medium than small tattoos. But in conveying a good impression of the relative magnitudes of the differences, they have some limitations. Also pie charts are useful only for displaying a limited number of categories, as the next section illustrates.
3.2 Pie charts: Nuclear power stations
Figure 2 shows a pie chart of the number of nuclear power stations in countries where nuclear power is used, based on the data from Table 1.
It is not so easy to extract meaningful information from this more detailed diagram. You can pick out the main users of nuclear power, and that is about all.
When trying to construct pie charts for data with many categories, a common ploy of the graphic designer is to produce a pie chart which displays the main contributors and lumps together the smaller ones. However, the process inevitably involves loss of information.
3.3 Bar charts: nuclear power stations
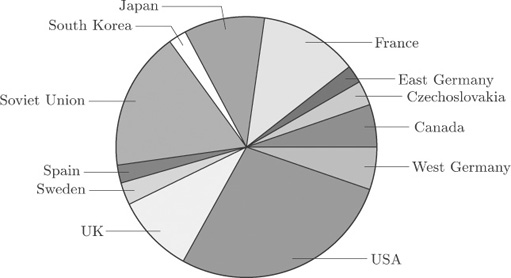
A better way of displaying the data on nuclear power stations is by constructing a rectangular bar for each country, the length of which is proportional to the count. Bars are drawn separated from each other. In this context, the order of the categories (countries) in the original data table does not matter, so the bars in Figure 3 have been drawn in order of decreasing size from top to bottom. This makes the categories easier to compare with one another.
The display in Figure 3 is called a bar chart. The bars may be drawn vertically or horizontally according to preference and convenience. Those in Figure 3 have been drawn horizontally because of the lengths of the names of some of the countries. If the bars had been drawn vertically, the names of the countries would not have fitted along the horizontal axis unless the bars had been drawn far apart or the names had been printed vertically. The former would have made comparison difficult, while the latter would have made the names difficult to read. However, it is conventional to draw the bars vertically whenever possible.
3.4 Bar charts: Surgical removal of tattoos
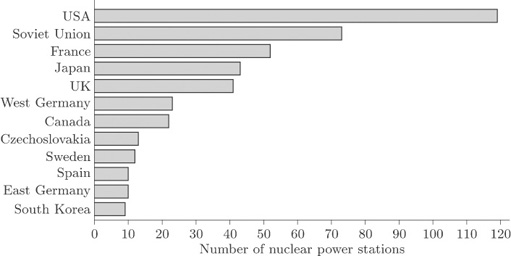
Figure 4 shows a bar chart for the data in Table 7 on the effectiveness of tattoo removal.
For the data on nuclear power stations, the order of the categories did not matter. However, sometimes order is important. The quality of tattoo removal was given a score from 1 to 4, and this ordering has been preserved along the quality (horizontal) axis. The vertical axis shows the reported frequency for each assessment.
The eye is good at assessing lengths, whereas comparison of areas or angles does not come so naturally. Thus an advantage of bar charts over pie charts is that it is much easier to be accurate when comparing frequencies from a bar chart than from a pie chart.
3.5 Problems with graphics
In this subsection we consider, briefly, some problems that can arise with certain ways of drawing bar charts and pie charts.
Figure 5 shows what is essentially the same bar chart as Figure 4, for the data on quality of tattoo removal. This time, though, the bar chart has been drawn in such a way as to suggest that the bars are ‘really’ three-dimensional. You can see that, compared to Figure 4, it is quite difficult to discern the corresponding frequency value for each bar.
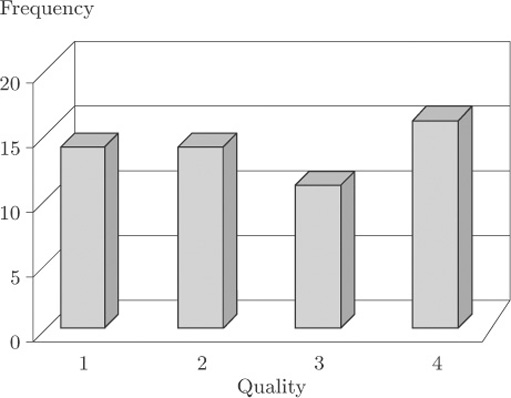
This kind of three-dimensional bar chart is commonly used as a graphic, in television reports or in the press, for showing data such as the results from an opinion poll on the popularity of the main political parties. Viewers or readers do not necessarily realise exactly how they are supposed to use the vertical scale to determine the heights of the bars. To interpret this kind of graphic properly, you need to be aware of how misleading it can be.
3.6 Problems with graphics: USA workforce
The danger of using three-dimensional effects is really brought home when two data sets are displayed on the same bar chart. Table 2 may be thought of as consisting of two data sets, one for male workers and one for female workers. On its own, each of these data sets could be portrayed in a bar chart like those you have seen earlier. However, one of the questions raised about these data in Activity 1 was how the data for men and for women could best be compared. Presenting them as two separate bar charts, one for males and one for females, is not the ideal way to support this comparison. We can produce a single bar chart that makes the comparison straightforward by plotting the corresponding bars for the two genders next to one another, and distinguishing the genders by shading, as in Figure 6.
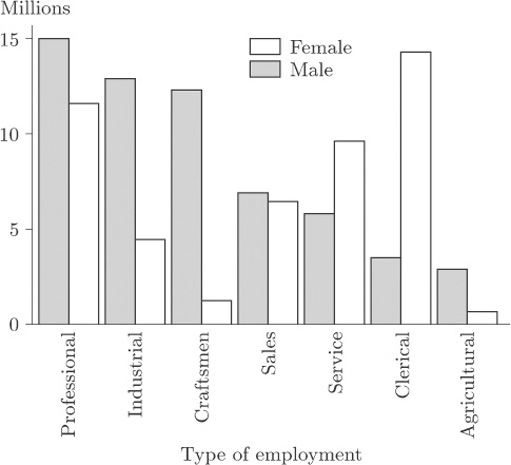
Activity 4: USA workforce
On the basis of Figure 6, describe how the balance between the genders differs from one ‘employment type’ to another.
Discussion
This display clearly shows the predominance of men in the Professional, Industrial, Craftsmen and Agricultural categories. In Service and Clerical women outnumber men and, in Clerical in particular, there is a huge imbalance. In Sales the numbers of men and women are very similar.
Figure 7 is an attempt to display the same information using a three-dimensional effect.
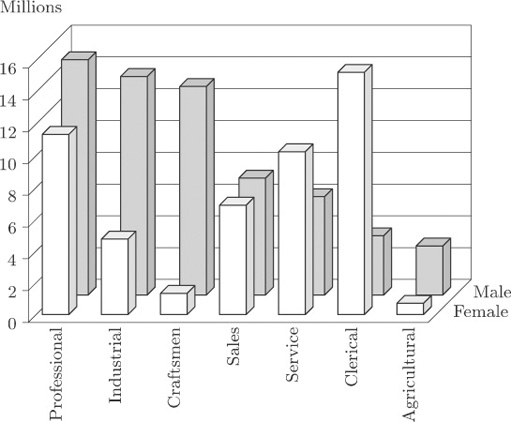
It is now much more difficult to identify values. Some blocks are hidden, which makes judgement difficult. The display for Sales is particularly misleading; in Figure 6 you can see that the bars are almost the same height, but in Figure 7 this is much less obvious.
Similar, and in some cases even more severe, problems arise with ‘three-dimensional’ pie charts.
3.7 Problems with graphics: nuclear power stations
Figure 8 shows a pie chart of the data on nuclear power stations from Table 1. This diagram is similar to Figure 2, except that the data for all countries apart from the five with the largest numbers of power stations have been amalgamated into a single ‘Others’ category.
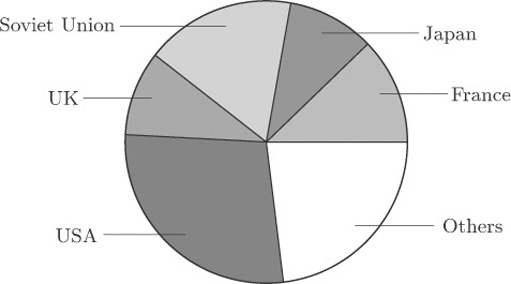
Figure 9 shows two attempts to display the same information in a ‘three-dimensional’ form. Can you see how they differ from one another?
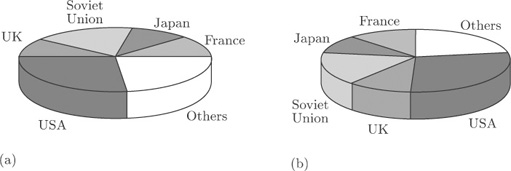
The only difference is the location of the ‘slices’. In Figure 9(b) they have been turned round through an angle of 90 degrees, compared to Figure 9(a). Yet this changes the whole appearance of the diagram. For instance, at first glance the UK ‘slice’ looks rather bigger in Figure 9(b) than that in Figure 9(a), and the Soviet Union ‘slice’ looks bigger in Figure 9(a) than that in Figure 9(b). In both cases, the differences are apparent rather than real, and are due to the angles at which the ‘slices’ are being viewed. To make comparisons between the sizes of different categories is not as straightforward as it might be even in Figure 8, because the human perception system finds it harder, on the whole, to compare angles than to compare lengths (as in a bar chart). But when you look at Figure 9(a), or Figure 9(b), you are being asked to make comparisons in a representation, on two-dimensional paper, of angles at an oblique direction to the direction in which you are looking. It is a tribute to the robustness of the human perception system that we can do this at all; but it is far from easy to do it accurately. ‘Three-dimensional’ charts might superficially look nicer, but they can be seriously misleading.
3.8 Pie charts and bar charts: summary
Two common display methods for data relating to a set of categories have been introduced in this section. In a pie chart, the number in each category is proportional to the angle subtended at the centre of the circular chart by the corresponding ‘slice’. In a bar chart, the number in each category is proportional to the length of the corresponding bar. The bars may be arranged vertically or horizontally, though it is conventional to draw them vertically where the labelling of the chart makes this practicable. You have seen that attempts to make pie charts and bar charts look ‘three-dimensional’ can make them considerably harder to interpret.
4 Histograms and scatterplots
In this section, two more kinds of graphical display are introduced – histograms in section 3.2 and scatterplots in section 3.3. Both are most commonly used with data that do not relate to separate categories, unlike pie charts and bar charts. However, as you will see, histograms do have something in common with bar charts. Scatterplots are a very common way of picturing the way in which two different quantities are related to each other.
4.1 Histograms
It is a fundamental principle in modern practical data analysis that all investigations should begin, wherever possible, with one or more suitable diagrams of the data. Such displays should certainly show overall patterns or trends, and should also be capable of isolating unexpected features that might otherwise be missed. The histogram is a commonly-used display, which is useful for identifying characteristics of a data set. To illustrate its use, we return to the data set on infants with SIRDS that we looked at briefly in Section 1.4.
The birth weights of 50 infants with severe idiopathic respiratory distress syndrome were given in Table 3. The list of weights is in itself not very informative, partly because there are so many weights listed. Suppose, however, that the weights are grouped as shown in Table 8.
| Group | Birth weight (kg) | Frequency |
|---|---|---|
| 1 | 1.0–1.2 | 6 |
| 2 | 1.2–1.4 | 6 |
| 3 | 1.4–1.6 | 4 |
| 4 | 1.6–1.8 | 8 |
| 5 | 1.8–2.0 | 4 |
| 6 | 2.0–2.2 | 3 |
| 7 | 2.2–2.4 | 4 |
| 8 | 2.4–2.6 | 6 |
| 2.6–2.8 | 3 | |
| 10 | 2.8–3.0 | 2 |
| 11 | 3.0–3.2 | 2 |
| 12 | 3.2–3.4 | 0 |
| 13 | 3.4–3.6 | 1 |
| 14 | 3.6–3.8 | 1 |
Such a table is called a grouped frequency table. Each listed frequency gives the number of individuals falling into a particular group: for instance, there were six children with birth weights between 1.0 and 1.2 kilograms. It may occur to you that there is an ambiguity over borderlines, or cutpoints, between the groups. Into which group, for example, should a value of 2.2 go? Should it be included in Group 6 or Group 7? Providing you are consistent with your rule over such borderlines, it really does not matter.
In fact, among the 50 infants there were two with a recorded birth weight of 2.2 kg and both have been allocated to Group 7. The infant weighing 2.4 kg has been allocated to Group 8. The rule followed here was that borderline cases were allocated to the higher of the two possible groups.
With the data structured like this, certain characteristics can be seen even though some information has been lost. There seems to be an indication that there are two groupings divided somewhere around 2 kg or, perhaps, three groupings divided somewhere around 1.5 kg and 2 kg. But the pattern is far from clear and needs a helpful picture, such as a bar chart. The categories are ordered, and notice also that the groups are contiguous (1.0–1.2, 1.2–1.4, and so on). This reflects the fact that here the variable of interest (birth weight) is not a count but a measurement.
The distinction between ‘counting’ and ‘measuring’ is quite an important one. In later units we shall be concerned with formulating different models to express the sort of variation that occurs in different sampling contexts, and it matters that the model should be appropriate to the type of data. Data arising from measurements (height, weight, temperature, and so on) are called continuous data. Those arising from counts (family size, hospital admissions, nuclear power stations) are called discrete.
In this situation, where we have a grouped frequency table of continuous data, the bars of the bar chart are drawn without gaps between them, as in Figure 10.
This kind of bar chart, of continuous data which have been put into a limited number of distinct groups or classes, is called a histogram. In this example, the 50 data items were allocated to groups of width 0.2 kg: there were 14 groups. The classification was quite arbitrary. If the group classifications had been narrower, there would have been more groups each containing fewer observations; if the classifications had been wider, there would have been fewer groups with more observations in each group. The question of an optimal classification is an interesting one, and surprisingly complex.
How many groups should you choose for a histogram? If you choose too many, the display will be too fragmented to show an overall shape. But if you choose too few, you will not have a picture of the shape: too much of the information in the data will be lost.
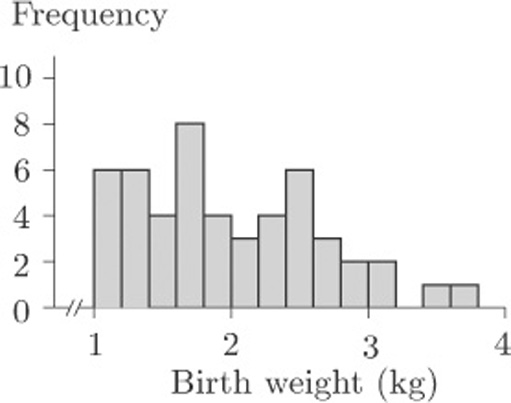
When these data were introduced in section 1.4, the questions posed were as follows. Do the children split into two identifiable groups? And is it possible to relate the chances of survival to birth weight? We are not, as yet, in a position to answer these questions, but we can see that the birth weights might split into two or even three ‘clumps’. On the other hand, can we be sure that this is no more than a consequence of the way in which the borderlines for the groups were chosen? Suppose, for example, we had decided to make the intervals of width 0.3 kg instead of 0.2 kg. We would have had fewer groups, with Group 1 containing birth weights from 1.0 to 1.3 kg, Group 2 containing birth weights from 1.3 to 1.6 kg, and so on, producing the histogram in Figure 11.
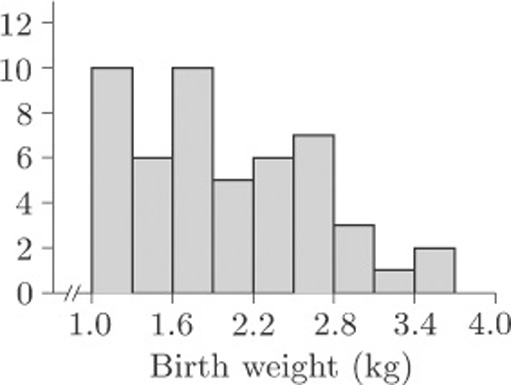
The histogram in Figure 11 looks quite different to that in Figure 10, but then this is not surprising as the whole display has been compressed into fewer bars. The basic shape remains similar, so you might be tempted to conclude that the choice of grouping does not really matter. But suppose we retain groupings of width 0.3 kg and choose a different starting point. Suppose we make Group 1 go from 0.8 to 1.1kg, Group 2 from 1.1 to 1.4kg, and so on. The resulting histogram is shown in Figure 12(a). In Figure 12(b), the groups again have width 0.3kg, but this time the first group starts at 0.9 kg.
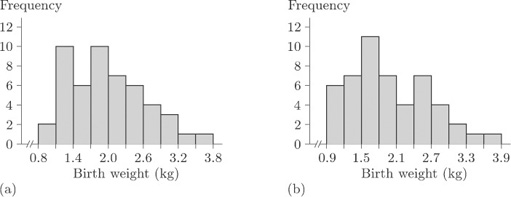
Activity 5: Comparing histograms
What information do the histograms in Figures 10, 11 and 12 give about the possibility that the children are split into two (or more) identifiable groups on the basis of birth weight?
Discussion
You might have felt that only Figures 10 and 12(b) give a really clear indication that the data are split into two ‘clumps’. Figures 10, 11 and 12(a) all give, to varying degrees, the impression that there is perhaps an identifiable group of babies with particularly low birth weights.
What you have seen in Figures 10 to 12 is a series of visual displays of a data set which warn you against trying to reach firm conclusions from histograms. It is important to realise that histograms often produce only a vague impression of the data – nothing more. One of the problems here is that we have only 50 data values, which is not really enough for a clear pattern to be evident. However, the histograms all convey one very important message: the data do not appear in a single, concentrated clump. Clearly it is a good idea to look at the way frequencies of data, such as the birth weights, are distributed and, given that a statistical computer package will quickly produce a histogram for you, comparatively little effort is required. This makes the histogram a valuable analytic tool and, in spite of some disadvantages, you will find that you use it a great deal.
It is, of course, quite feasible to produce grouped frequency tables and draw histograms by hand. However, the process can be very long-winded, and in practice statisticians almost always use a computer to produce them.
4.2 Scatterplots
In recent years, graphical displays have come into prominence because computers have made them quick and easy to produce. Techniques of data exploration have been developed which have revolutionised the subject of statistics, and today no serious data analyst would carry out a formal numerical procedure without first inspecting the data by eye. Nowhere is this demonstrated more forcibly than in the way a scatterplot reveals a relationship between two variables.
Look at Figure 13, which displays the data on cirrhosis and alcoholism from Table 5. This display is a scatterplot.
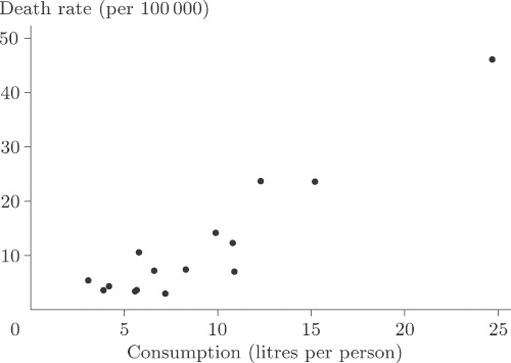
In a scatterplot, one variable is plotted on the horizontal axis and the other on the vertical axis. Each data item corresponds to a point in two-dimensional space. For example, the average annual consumption of alcohol in France for the time over which the data were collected was 24.7 litres per person, and the death rate per hundred thousand of the population through cirrhosis and alcoholism was 46.1. In this diagram consumption is plotted along the horizontal axis and death rate is plotted up the vertical axis. The data point at the coordinate (24.7,46.1) corresponds to France.
Is there a strong relationship between the two variables? In other words, do the points appear to fit fairly ‘tightly’ about a straight line or a curve? It is fairly obvious that there is a relationship, although the overall pattern is not easy to see since most of the points are concentrated in the bottom left-hand corner. There is one point that is a long way from the others and the size of the diagram relative to the page is dictated by the available space into which it must fit. We remarked upon this point, corresponding to France, when we first looked at the data, but seeing it here really does put into perspective the magnitude of the difference between France and the other countries. The best way to look for a general relationship between death rate and consumption of alcohol is to spread out the points representing the more conventional drinking habits of other countries by leaving France, an extreme case, out of the plot. The picture, given in Figure 14, is now much clearer. It shows up a general (and hardly surprising) rule that the incidence of death through alcohol-related disease is strongly linked to average alcohol consumption, the relationship being plausibly linear. A ‘linear’ relationship means that we could draw a straight line through the points that would fit them quite well, and this has been done in Figure 14.
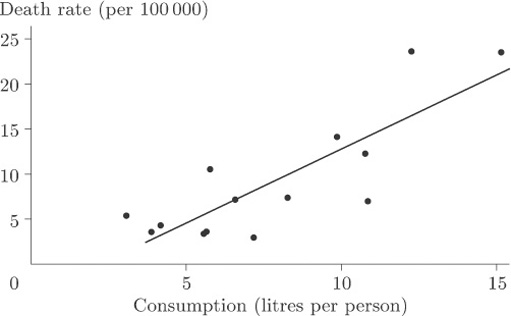
Of course, we would not expect the points to sit precisely on the line but to be scattered about it tightly enough for the relationship to show. In this case you could conclude that, given the average annual alcohol consumption in any country not included among those on the scatterplot, we would be fairly confident of being able to use our straight line for providing a reasonable estimate of the national death rate due to cirrhosis and alcoholism.
It is worth mentioning at this stage that demonstrating the existence of some sort of association is not the same thing as demonstrating causation; that, in this case, alcohol use ‘causes’ (or makes more likely) cirrhosis or an early death. For example, if cirrhosis were stress-related, so might be alcohol consumption, and hence the apparent relationship. It should also be noted that these data were averaged over large populations and (whatever may be inferred from them) they say nothing about the consequences of alcohol use for an individual.
France was left out because that data point was treated as an extreme case. It corresponded to data values so atypical, and so far removed from the others, that we were wary of using them to draw general conclusions.
‘Extreme’, ‘unrepresentative’, ‘atypical’ or possibly ‘rogue’ observations in sets of data are sometimes called outliers. It is important to recognise that, while we would wish to eliminate from a statistical analysis data points which were erroneous (wrongly recorded, perhaps, or observed when background circumstances had profoundly altered), data points that appear ‘surprising’ are not necessarily ‘wrong’. The identification of outliers, and what to do with them, is a research question of great interest to the statistician. Once a possible outlier has been identified, it should be closely inspected and its apparently aberrant behaviour accounted for. If it is to be excluded from the analysis there must be sound reasons for its exclusion. Only then can the data analyst be happy about discarding it. An example will illustrate the point.
4.3 Scatterplots: body weights and brain weights for animals
In our discussion of the data on body weights and brain weights for animals in section 1.7, we conjectured a strong relationship between these weights on the grounds that a large body might well need a large brain to run it properly. At that stage a ‘difficulty’ with the data was also suggested, but we did not say exactly what it was. It would, you might reasonably have thought, be useful to look at a scatterplot, but you will see the difficulty if you actually try to produce one. Did you spot the problem when it was first mentioned in section 1.7? There are many very small weights such as those for the hamster and the mouse which simply do not show up properly if displayed on the same plot as, say, those for animals like the elephant! Figure 15 shows the difficulty very clearly.
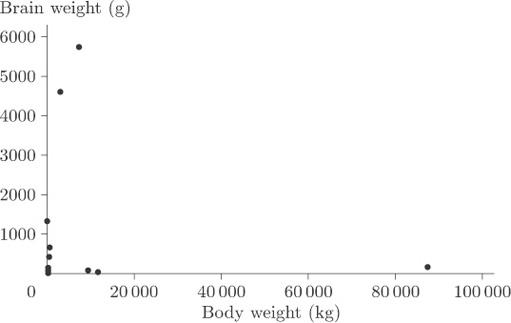
You cannot see anything from this scatterplot. The many very small weights are all lumped together in order to allow a sufficient spread on the scale to include the heavy ones on the plot. As it stands, the plot is pretty well useless.
Now, this sort of thing often happens and the usual way of getting round the problem is to transform the data in such a way as to spread out the points with very small values of either variable, and to pull closer together the points with very large values for either variable. The objective is to reduce the spread in the large values relative to the spread in the small values. In this case it can be done by plotting the logarithm of brain weight against the logarithm of body weight. The log transformation compresses the large values but stretches the small ones. (Notice that simply treating the large values as outliers and removing them would not solve the problem because the tight clumping of points close to the origin would still remain to some extent. Also, there are in this case several possible outliers, and in general it is not good practice simply to throw data out of an analysis without at least considering potential reasons why these points should not be considered along with all the rest.)
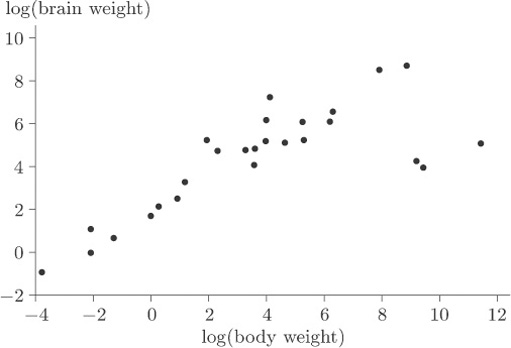
Figure 16 shows the scatterplot that is obtained after applying a log transformation to both variables.
Activity 6: Interpreting a scatterplot
What information does Figure 16 give about the relationship between body weight and brain weight? Are there any points that you might consider as outliers?
Discussion
The plot immediately reveals three apparent outliers to the right of the main band of points. Excluding these three species, there is a convincing linear relationship, although there are two or three points that are slightly above the general pattern of the others and hence appear to have high brain weight to body weight ratios.
When you discover the animals to which the three ‘obvious’ outlying points correspond you will not be surprised. One way of identifying them is by labelling all the animals with the first letters of the names of their species and plotting the letters in place of the points. The resulting scatterplot is shown in Figure 17.
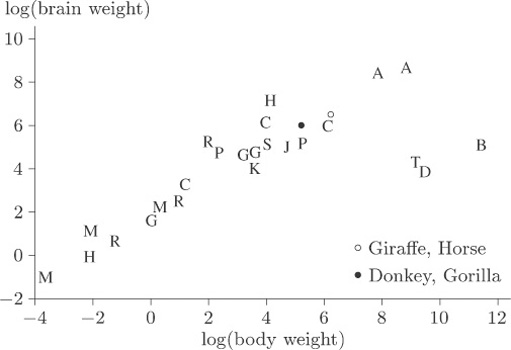
A comparison of the letters with the values in Table 6 shows that the three outliers, labelled B, D and T, correspond to the dinosaurs Brachiosaurus, Diplodocus and Triceratops. The human, mole and Rhesus monkey all appear to have rather high brain weight in relation to body weight, but they are by no means as extreme compared to the general pattern as are the three dinosaur species.
4.4 Histograms and scatterplots: summary
Two common graphical displays, most frequently used for continuous data (arising from measurements), have been introduced in this section. A histogram is in a sense a development of the idea of a bar chart. A set of continuous data is divided up into groups, the frequencies in the groups are found, and a histogram is produced by drawing vertical bars, without gaps between them, whose heights are proportional to the frequencies in the groups. You have seen that the shape of a histogram drawn from a particular data set can depend on the choices made for the grouping of the data.
Scatterplots represent the relationship between two variables. The variables generally have to be numerical, and are commonly continuous, though they may also be discrete (counted). One variable is plotted on the horizontal axis and the other on the vertical axis. One point is plotted, in the appropriate position, for each individual entity (person, animal, country) in the data set. As well as making it easy to identify any general pattern, such as a straight line, in the relationship between the variables, a scatterplot can help in the identification of outliers. These are data points that lie a long way from the general pattern in the data. In some cases, the patterns shown in a scatterplot can be made clearer by omitting an outlier, though this is very often not an advisable thing to do. In other cases, it may help to transform the data by applying some appropriate function to one or both of the variables involved.
5 Numerical summaries
Histograms provide a quick way of looking at data sets, but they lose sight of individual observations and they tend to play down ‘intuitive feel’ for the magnitude of the numbers themselves. We may often want to summarize the data in numerical terms; for example, we could use a number to summarize the general level (or location) of the values and, perhaps, another number to indicate how spread out or dispersed they are. In this section you will learn about some numerical summaries that are used for both of these purposes: measures of location are discussed in sections 4.2 to 4.5 and measures of dispersion in sections 4.6 to 4.9. In section 4.11 you will be introduced to the important concept of skewness (lack of symmetry) in a data set.
5.1 Measures of location
Everyone professes to understand what is meant by the term ‘average’, in that it should be representative of a group of objects. The objects may well be numbers from, say, a batch or sample of measurements, in which case the average should be a number which in some way characterises the batch as a whole. For example, the statement ‘a typical adult female in Britain is 160 cm tall’ would be understood by most people who heard it. Obviously not all adult females in Britain are the same height: there is considerable variation. To state that a ‘typical’ height is 160 cm is to ignore the variation and summarise the distribution of heights with a single number. Even so, it may be all that is needed to answer certain questions. (For example, is a typical adult female shorter than a typical adult male?)
But how should this representative value be chosen? Should it be a typical member of the group or should it be some representative measure which can be calculated from the collection of individual data values? Believe it or not, there are no straightforward answers to these questions. In fact, two different ways of expressing a representative value are commonly used in statistics, namely the median and the mean. The choice of which of these provides the better representative numerical summary is fairly arbitrary and is based entirely upon the nature of the data themselves, or the particular preference of the data analyst, or the use to which the summary statement is to be put. The median and the mean are both examples of measures of location of a data set; here the word ‘location’ is essentially being used in the sense of the position of a typical data value along some sort of coordinate axis.
We deal with the median and the mean in turn, as well as considering the concept of the mode of a data set. (In a sense the mode is another measure of location.)
5.2 The median
The median describes the central value of a set of data. Here, to be precise, we are discussing the sample median, in contrast to the population median.
The sample median
The median of a sample of data with an odd number of data values is defined to be the middle value of the data set when the values are placed in order of increasing size. If the sample size is even, then the median is defined to be halfway between the two middle values. In this course, the median is denoted by m
5.2.1 Beta endorphin concentration (collapsed runners)
The final column of Table 4 contains the blood plasma β endorphin concentrations for eleven runners who collapsed towards the end of the Great North Run. The observations are already sorted. They are as follows.
| 66 | 72 | 79 | 84 | 102 | 110 | 123 | 144 | 162 | 169 | 414 |
Eleven is an odd number, so the middle value of the data set is the sixth value (five either side). So, in this case, the sample median is 110 pmol/l.
5.2.2 Birth weights of infants with SIRDS
The data in Table 3 are the birth weights (in kg) of 50 infants suffering from severe idiopathic respiratory distress syndrome. There are two groups of infants: those who survived the condition (there were 23 of these) and those who, unfortunately, did not. The data have not been sorted, and it is not an entirely trivial exercise to do this by hand (though it is a task that a computer can handle very easily). The sorted data are given in Table 9.
| 1.030* | 1.300* | 1.720 | 2.090 | 2.570 |
| 1.050* | 1.310* | 1.750* | 2.200* | 2.600 |
| 1.100* | 1.410 | 1.760 | 2.200 | 2.700 |
| 1.130 | 1.500* | 1.770* | 2.270* | 2.730* |
| 1.175* | 1.550* | 1.820* | 2.275* | 2.830 |
| 1.185* | 1.575 | 1.890* | 2.400 | 2.950 |
| 1.225* | 1.600* | 1.930 | 2.440* | 3.005 |
| 1.230* | 1.680 | 1.940* | 2.500* | 3.160 |
| 1.262* | 1.715 | 2.015 | 2.550 | 3.400 |
| 1.295* | 1.720* | 2.040 | 2.560* | 3.640 |
| * child died | ||||
The sample size is even: the sample median is defined to be the value halfway between the 25th and 26th observations. That is to say, it is obtained by splitting the difference between 1.820 (the 25th value) and 1.890 (the 26th value). This gives
½(1.820 + 1.890) = 1.855kg
Activity 7: Birth weights of infants with SIRDS
Find the median birth weight for the infants who survived, and for those who did not.
Answer
There were 23 children who survived the condition. Their birth weights are 1.130, 1.410, 1.575, 1.680, 1.715, 1.720, 1.760, 1.930, 2.015, 2.040, 2.090, 2.200, 2.400, 2.550, 2.570, 2.600, 2.700, 2.830, 2.950, 3.005, 3.160, 3.400, 3.640. The median birth weight for these children is 2.200 kg (the 12th value in the sorted list).
There were 27 children who died. The sorted birth weights are 1.030, 1.050, 1.100, 1.175, 1.185, 1.225, 1.230, 1.262, 1.295, 1.300, 1.310, 1.500, 1.550, 1.600, 1.720, 1.750, 1.770, 1.820, 1.890, 1.940, 2.200, 2.270, 2.275, 2.440, 2.500, 2.560, 2.730. The middle value is the 14th (thirteen either side) so the median birth weight for the children who died is 1.600 kg.
Activity 8: Beta endorphin concentration (successful runners)
The first two columns of Table 4 give the blood plasma β endorphin concentrations of eleven runners before and after completing the Great North Run successfully. There is a marked difference between these concentrations. The data are reproduced in Table 10 below with the ‘After – Before’ differences also shown.
| Before | 4.3 | 4.6 | 5.2 | 5.2 | 6.6 | 7.2 | 8.4 | 9.0 | 10.4 | 14.0 | 17.8 |
| After | 29.6 | 25.1 | 15.5 | 29.6 | 24.1 | 37.8 | 20.2 | 21.9 | 14.2 | 34.6 | 46.2 |
| Difference | 25.3 | 20.5 | 10.3 | 24.4 | 17.5 | 30.6 | 11.8 | 12.9 | 3.8 | 20.6 | 28.4 |
Find the median of the ‘After – Before’ differences given in Table 10.
Answer
The ordered differences are 3.8, 10.3, 11.8, 12.9, 17.5, 20.5, 20.6, 24.4, 25.3, 28.4, 30.6. The median difference is 20.5 pmol/l.
5.3 The mean
The second measure of location defined in this course for a collection of data is the mean. Again, to be precise, we are discussing the sample mean, as opposed to the population mean. This is what most individuals would understand by the word ‘average’. All the items in the data set are added together, giving the sample total. This total is divided by the number of items (the sample size).
The sample mean
The mean of a sample is the arithmetic average of the data values. It is obtained by adding together all of the data values and dividing this total by the number of items in the sample.
If the n items in a data set are denoted x 1, x 2,…, xn , then the sample size is n, and the sample mean, which is denoted ![]() , is given by
, is given by
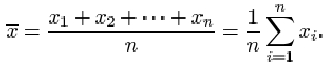
The symbol ![]() denoting the sample mean is read ‘x-bar’.
denoting the sample mean is read ‘x-bar’.
Recall that the symbol for the Greek upper-case letter sigma Σ is used to mean ‘the sum of’. The expression
which reads ‘sigma i equals 1 to n’, means the sum of the terms x 1, x 2,…, x n .
From the data in Table 4 (repeated at the start of section 4.2), the mean β endorphin concentration (in pmol/l) of collapsed runners is
Activity 9: Beta endorphin concentration (successful runners)
Find the mean of the ‘After – Before’ differences given in Table 10.
Answer
Solution
The mean ‘After – Before’ difference (in pmol/l) is
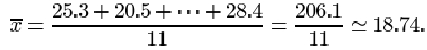
Two plausible measures of location have been defined for describing a typical or representative value for a sample of data. Which measure should be chosen in a statement of that typical value? In the examples we have looked at in this section, there has been little to choose between the two. Are there principles that should be followed? As you might expect there are no hard and fast rules: it all depends on the data that we are trying to summarise, and our aim in summarising them.
To a large extent deciding between using the sample mean and the sample median depends on how the data are distributed. If their distribution appears to be regular and concentrated in the middle of their range, the mean is usually used. When a computer is not available, the mean is easier to calculate than the median because no sorting is involved and, as you will see later in the course, it is easier to use for drawing inferences about the population from which the sample has been taken.
If, however, the data are irregularly distributed with apparent outliers present, then the sample median is often preferred in quoting a typical value, since it is less sensitive to such irregularities. You can see this by looking again at the data on collapsed runners in Table 4. The mean endorphin concentration is 138.6 pmol/l, whereas the median concentration is 110. The large discrepancy is due to the outlier with an endorphin concentration of 414. Excluding this outlier brings the mean down to 111.1 while the median decreases to 106. From this we see that the median is more stable than the mean in the sense that outliers exert less influence upon it. The word resistant is sometimes used to describe measures which are insensitive to outliers. The median is said to be a resistant measure, whereas the mean is not resistant.
A general comment on the use of certain familiar words in statistics is appropriate here. Notice the use of the word ‘range’ in the second paragraph after Activity 9. The statement made there is a statement of the extent of the values observed in a sample, as in ‘the observed weights ranged from a minimum of 1.03kg to a maximum of 3.64kg’. It need not be an exact statement: ‘the range of observed weights was from 1kg to about 4 kg’. However, in Subsection 4.6 you will see the word ‘range’ used in a technical sense, as a measure of dispersion in data. This often happens in statistics: a familiar word is given a technical meaning. Terms you will come across later in the course include expectation, likelihood, confidence, estimator, significant. But we would not wish this to preclude normal English usage of such words. It will usually be clear from the context when the technical sense is intended.
5.4 The mode
The USA workforce data in Table 2 were usefully summarised in Figure 6, which is reproduced below as Figure 18.
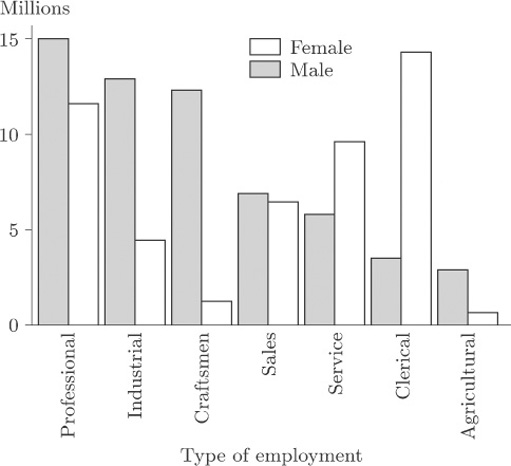
The variable recorded here is ‘type of employment’ (professional, industrial, clerical, and so on) so the data are categorical and not amenable to ordering. In this context the notion of ‘mean type of employment’ or ‘median type of employment’ is not a sensible one. For any data set, a third representative measure which is sometimes used is the mode. It describes the most frequently occurring observation. Thus, for males in employment in the USA during 1986, the modal type of employment was ‘professional’ while, for females, the modal type of employment was ‘clerical’.
The word mode can also reasonably be applied to numerical data, referring again to the most frequently occurring observation. But there is a problem of definition. For the birth weight data in Table 3, there were two duplicates: two of the infants weighed 1.72 kg, and another two weighed 2.20 kg. So there would appear to be two modes, and yet to report either one of them as a representative weight is to make a great deal of an arithmetic accident. If the data are classified into groups, then you can see from Figures 10 to 12 in section 3.1 that even the definition of a ‘modal group’ will depend on the definition of borderlines (and on what to do with borderline cases). The number of histogram peaks as well as their locations can alter.
Yet it often happens that a collection of data presents a very clear picture of an underlying pattern, and one which would be robust against changes in group definition. In such a case it is common to identify as modes not just the most frequently occurring observation (the highest peak) but every peak. Here are two examples.
5.4.1 Chest measurements of Scottish soldiers
Figure 19 shows a histogram of chest measurements (in inches) of a sample of 5732 Scottish soldiers.
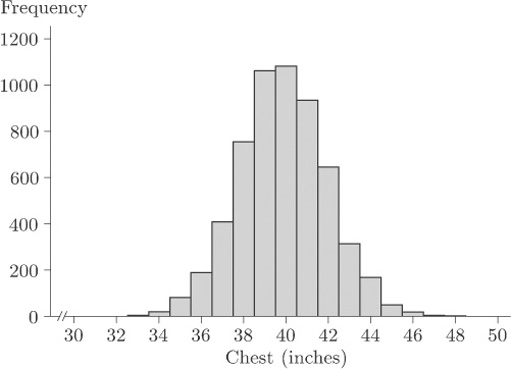
This data set is discussed further later in the course; for the moment, simply observe that there is an evident single mode at around 40 inches. The data are said to be unimodal.
5.4.2 Waiting times between geyser eruptions
Figure 20 shows a histogram of waiting times, varying from about 40 minutes to about 110 minutes.
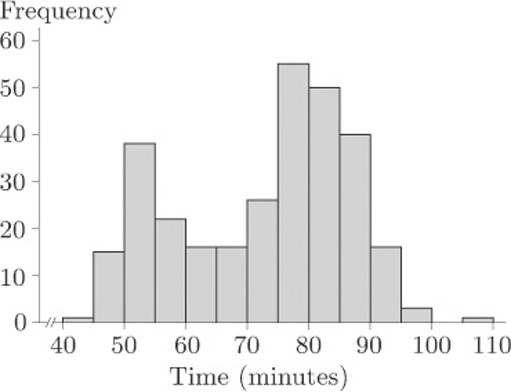
In fact, these are waiting times between the starts of successive eruptions of the Old Faithful geyser in the Yellowstone National Park, Wyoming, USA, during August, 1985. Observe the two modes. These data are said to be bimodal.
Sometimes data sets may exhibit three modes (trimodal) or many modes (multimodal). You should be wary of too precise a description. Both the data sets in Figures 19 and 20 were based on large samples, and their message is unambiguous. As you will see later in the course, smaller data sets can give rise to very jagged histograms indeed, and any message about one or more preferred observations is consequently very unclear.
5.5 Measures of dispersion
During the above discussion of suitable numerical summaries for a typical value (measures of location), you may have noticed that it was not possible to make any kind of decision about the relative merits of the sample mean and median without introducing the notion of the extent of variation of the data. In practice, this means that the amount of information contained in these measures, when taken in isolation, is not sufficient to describe the appearance of the data. A more informative numerical summary is needed. In other words, if we are to be happy about replacing a full data set by a few summary numbers, we need some measure of the dispersion, sometimes called the spread, of observations.
The range is the difference between the smallest and largest data values. It is certainly the simplest measure of dispersion, but it can be misleading. The range of β endorphin concentrations for collapsed runners is 414−66=348, suggesting a fairly wide spread. However, omitting the value 414 reduces the range to 169−66=103. This sensitivity to a single data value suggests that the range is not a very reliable measure; a much more modest assessment of dispersion may be more appropriate. By its very nature, the range is always going to give prominence to outliers and therefore cannot sensibly be used in this way.
This example indicates the need for an alternative to the range as a measure of dispersion, and one which is not over-influenced by the presence of a few extreme values. In fact, we shall discuss in turn two different measures of dispersion: the interquartile range and the standard deviation.
5.6 Quartiles and the interquartile range
The first alternative measure of dispersion we shall discuss is the interquartile range: this is the difference between summary measures known as the lower and upper quartiles. The quartiles are simple in concept: if the median is regarded as the middle data point, so that it splits the data in half, the quartiles similarly split the data into quarters. This is, of course, an over-simplification. With an even number of data points, the median is defined to be the average of the middle two: defining quartiles is a little more complicated.
It would be convenient to express our wordy definition of the median in a concise symbolic form, and this is easy to do. Any data sample of size n may be written as a list of numbers
x 1,x 2,x 3, ... x n
In order to calculate the sample median it is necessary to sort the data so that they are written in order of increasing size. The sorted list can then be written as
x (1),x (2),x (3), ... x (n)
where x (1) is the smallest value in the original list (the minimum) and x (n) is the largest (the maximum). In general, the notationx (p) is used to mean the pth value when the data are arranged in order of increasing size. Each successive item in the ordered list is greater than or equal to the previous item. For instance, the list of six data items
7, 1, 3, 6, 3, 7
may be ordered as
1, 3, 3, 6, 7, 7
So, for these data, x (1)=1, x (2)=x (3)=3, x (4)=6, x (5)=x (6)=7.
In any such ordered list, the sample median m may be defined to be the number
m = x (½(n + 1))
as long as the subscript on the right-hand side is appropriately interpreted.
If the sample size n is odd, then the number ½(n+1) is an integer, and there is no problem of definition. For instance, if n=27 then ½(n+1)=14, and the sample median is m = x (14) side of it.
If the sample size n is even then the number ½(n+1) is not an integer but has a fractional part equal to ½. For instance, if n = 6 (as in the example above) then the sample median is
m = x (½(n+1)) = x (3½).
Such numbers are sometimes called ‘half-integer’
If the number x (3½) is interpreted as ‘the number halfway between x (3) and x (4)’ then you can see that the wordy definition survives intact. This obvious interpretation of numbers such as x 3½ can be extended to numbers such as x (2¼) and x (4¾): x (2¼) is the number one-quarter of the way from x (2) to x (3), and x (4¾) is the number three-quarters of the way from x (4) to x (5). Interpreting fractional subscripts in this way when they occur, the lower quartile (roughly, one-quarter of the way into the data set) and the upper quartile (approximately three-quarters of the way through the data set) may be defined as follows.
Sample quartiles
If a data set x 1, x 2,… , x n is reordered as x (1), x (2), …, x (n) , where
x (1) ≤ x (2) ≤ ... ≤ x(n)
then the lower sample quartile qL is defined by
qL = x (¼(n+1))
and the upper sample quartile qU is defined by
qU = x (¾(n+1))
Unfortunately, there is no universally accepted definition for sample quartiles, nor, indeed, a universally accepted nomenclature. The lower and upper sample quartiles are sometimes called the first and third sample quartiles. The median is the second sample quartile. Other definitions are possible, and you may even be familiar with some of them. For instance, some practitioners use
qL = x (¼n+½), qU = x (¾n+½)
Others use
qL = x (¼n+¾), qU = x (¾n+¼)
Still others insist that the lower and upper quartiles be defined in such a way that they are identified uniquely with actual sample items. However, almost all definitions of the sample median reduce to the same thing.
5.6.1 Quartiles for the SIRDS data
For the 23 infants who survived SIRDS, the ordered birth weights are given in Table 9. The first quartile is
qL = x (¼(23+1)) = x (6) = 1.720kg.
The third quartile is
qU = x (¾(23+1)) = x (18) = 2.830kg.
5.6.2 Quartiles when the sample size is awkward
For the six ordered data items 1, 3, 3, 6, 7, 7, the lower quartile is given by
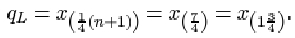
In other words, the lower quartile qL is given by the number three-quarters of the way between x (1)=1 and x (2)=3. The difference between x (1) and x (2) is 2, so
qL = x (1) + ¾(x (2) – x (1)) = 1 + ¾ × 2 = 2.5.
The upper quartile is given by
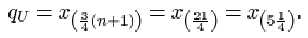
So the upper quartile qu is the number one-quarter of the way between x (5)=7 and x (6)=7. This is just the number 7 itself.
Having defined the quartiles, it is straightforward to define the measure of dispersion based on them: the interquartile range is the difference between the quartiles.
The interquartile range
The interquartile range, which is a measure of the dispersion in a data set, is the difference qU−qL between the upper quartile qU and the lower quartile qL.
5.6.3 Interquartile range for the SIRDS data
For the 23 infants who survived SIRDS, the lower quartile is qL=1.720 kg, and the upper quartile is qU=2.830 kg. Thus the interquartile range (in kg) is
qU – qL = 2.830 – 1.720 = 1.110.
Activity 10: More on the SIRDS data
Find the lower and upper quartiles, and the interquartile range, for the birth weight data on those children with SIRDS who died. The ordered data are in Table 9.
Answer
Solution
The lower quartile birth weight (in kg) for the 27 children who died is given by
qL = x (¼(n+1)) = x (7) = 1.230.
The upper quartile birth weight (in kg) is
qU = x (¾(n+1)) = x (21) = 2.220.
The interquartile range (in kg) is
qU – qL = 2.200 – 1.230 = 0.970.
Activity 11: Chondrite meteors
Find the median, the lower and upper quartiles, and the interquartile range for the data in Table 11, which give the percentage of silica found in each of 22 chondrite meteors. (The data are ordered.)
| 20.77 | 22.56 | 22.71 | 22.99 | 26.39 | 27.08 | 27.3 | 27.33 |
| 27.57 | 27.81 | 28.69 | 29.36 | 30.25 | 31.89 | 32.88 | 33.23 |
| 33.28 | 33.40 | 33.52 | 33.83 | 33.95 | 34.82 |
(Good, I.J. and Gaskins, R.A. (1980) Density estimation and bump-hunting by the penalized likelihood method exemplified by scattering and meteorite data. J. American Statistical Association, 75, 42–56.)
Answer
Solution
For the silica data, the sample size n is 22. The lower quartile is
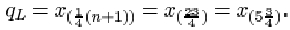
So qL is three-quarters of the way between
x (5)=26.39 and x (6)=27.08. That is
qL = 26.39 + ¾(27.08 – 26.39) = 26.9075,
or approximately 26.91. The sample median is
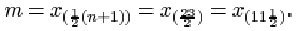
This is midway between x (11)=28.69 and x (12)=29.36. That is 29.025, or approximately 29.03.
The upper quartile is
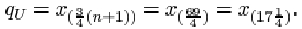
So qU is one-quarter of the way between x (17)=33.28 and x (18)=33.40. That is
qU = 33.28 + ¼(33.40 – 33.28) = 33.31
The interquartile range is
qU – qL = 33.31 – 26.9075 = 6.4025,
or approximately 6.40.
5.7 The standard deviation
The interquartile range is a useful measure of dispersion in the data and it has the excellent property of not being too sensitive to outlying data values. (That is, it is a resistant measure.) However, like the median it does suffer from the disadvantage that its calculation involves sorting the data. This can be very time-consuming for large samples when a computer is not available to do the calculations. A measure that does not require sorting of the data and, as you will find in later units, has good statistical properties is the standard deviation.
The standard deviation is defined in terms of the differences between the data values (xi) and their mean ![]() . These differences
. These differences ![]() , which may be positive or negative, are called residuals.
, which may be positive or negative, are called residuals.
Example 1 Calculating residuals
The mean difference in β endorphin concentration for the eleven runners in section 1.4 who completed the Great North Run is 18.74 pmol/l (to two decimal places). The eleven residuals are given in the following table.
| Difference, xi | 25.3 | 20.5 | 10.3 | 24.4 | 17.5 | 30.6 | 11.8 | 12.9 | 3.8 | 20.6 | 28.4 |
| Mean, | 18.74 | 18.74 | 18.74 | 18.74 | 18.74 | 18.74 | 18.74 | 18.74 | 18.74 | 18.74 | 18.74 |
| Residual, | 6.56 | 1.76 | −8.44 | 5.66 | −1.24 | 11.86 | −6.94 | −5.84 | −14.94 | 1.86 | 9.66 |
For a sample of size n consisting of the data values x (1), x (2), …, x(n) and having mean ![]() , the ith residual may be written as
, the ith residual may be written as
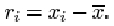
These residuals all contribute to an overall measure of dispersion in the data. Large negative and large positive values both indicate observations far removed from the sample mean. In some way they need to be combined into a single number.
There is not much point in averaging them: positive residuals will cancel out negative ones. In fact their sum is zero, since
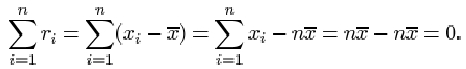
Therefore their average is also zero. What is important is the magnitude of each residual, the absolute difference ![]() . The absolute residuals could be added together and averaged, but this measure (known as the mean absolute deviation) does not possess very convenient mathematical properties. Another way of eliminating minus signs is by squaring the residuals. If these squares are averaged and then the square root is taken, this will lead to a measure of dispersion known as the sample standard deviation. It is defined as follows.
. The absolute residuals could be added together and averaged, but this measure (known as the mean absolute deviation) does not possess very convenient mathematical properties. Another way of eliminating minus signs is by squaring the residuals. If these squares are averaged and then the square root is taken, this will lead to a measure of dispersion known as the sample standard deviation. It is defined as follows.
The sample standard deviation
The sample standard deviation, which is a measure of the dispersion in a sample x 1, x 2, …, xn with sample mean ![]() , is denoted by s and is obtained by averaging the squared residuals, and taking the square root of that average. Thus, if
, is denoted by s and is obtained by averaging the squared residuals, and taking the square root of that average. Thus, if ![]() , then
, then
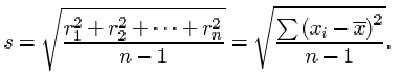
There are two important points you should note about this definition. First and foremost, although there are n terms contributing to the sum in the numerator, the divisor used when averaging the residuals is not the sample size n, but n−1. The reason for this surprising amendment will become clear later in the course. Whether dividing by n or by n−1, the measure of dispersion obtained has useful statistical properties, but these properties are subtly different. The definition above, with divisor n−1, is used in this course.
Second, you should remember to take the square root of the average. The reason for taking the square root is so that the measure of dispersion obtained is measured in the same units as the data. Since the residuals are measured in the same units as the data, their squares and the average of their squares are measured in the squares of those units. So the standard deviation, which is the square root of this average, is measured in the same units as the data.
Example 2 Calculating the standard deviation
The sum of the squared residuals for the eleven β endorphin concentration differences is
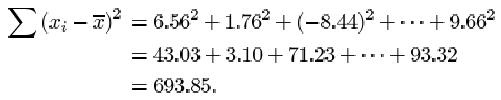
Notice that a negative residual contributes a positive value to the calculation of the standard deviation. This is because it is squared.
So the sample standard deviation of the differences is
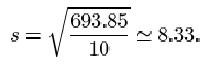
Even for relatively small samples the arithmetic is rather awkward if done by hand. Fortunately, it is now common for calculators to have a ‘standard deviation’ button, and all that is required is to key in the data. The exact details of how to do this differ between different models and makes of calculator. Several types of calculator give you the option of using either n or n−1 as the divisor. You should check that you understand exactly how your own calculator is used to calculate standard deviations. Try using it to calculate the sample standard deviation of the eleven β endorphin concentration differences for runners who completed the race, using n−1 as the divisor. Make sure that you get the same answer as given above (that is, 8.33).
Activity 12: Calculating standard deviations
Use your calculator to calculate the standard deviation for the β endorphin concentrations of the eleven collapsed runners. The data in pmol/l, originally given in Table 4, are as follows.
| 66 | 72 | 79 | 84 | 102 | 110 | 123 | 144 | 162 | 169 | 414 |
Answer
Solution
Answering this question might involve delving around for the instruction manual that came with your calculator! The important thing is not to use the formula — let your calculator do all the arithmetic. All you should need to do is key in the original data and then press the correct button. (There might be a choice, one of which is when the divisor in the ‘standard deviation’ formula is n, the other is when the divisor is n−1. Remember, in this course we use the second formula.) For the collapsed runners’ β endorphin concentrations, s = 98.0.
You will find that the main use of the standard deviation lies in making inferences about the population from which the sample is drawn. Its most serious disadvantage, like the mean, results from its sensitivity to outliers.
Activity 13: Calculating standard deviations
In Activity 12 you calculated a standard deviation of 98.0 for the data on the collapsed runners. Try doing the calculation again, but this time omit the outlier at 414. Calculate also the interquartile range of this data set, first including the outlier and then omitting it.
Answer
Solution
When the outlier of 414 is omitted, you will find a drastic reduction in the standard deviation from 98.0 to 37.4, a reduction by a factor of almost three!
The data are given in order in Activity 12. For the full data set, the sample size n is 11. The lower quartile is
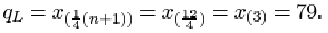
The upper quartile is
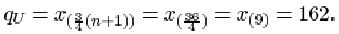
Thus the interquartile range is
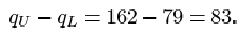
When the outlier 414 is omitted from the data set, the sample size n is 10. The lower quartile is
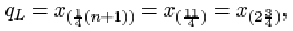
which is three-quarters of the way between x (2)=72 and x (3) = 79. Thus
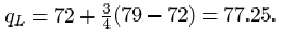
The upper quartile is
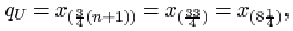
which is one-quarter of the way between x (8)=144 and x (9)=162. So
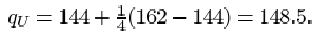
The interquartile range is
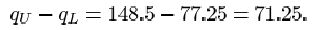
Naturally it has decreased with the removal of the outlier, but the decrease is relatively far less than the decrease in the standard deviation.
You should have found a considerable reduction in the standard deviation when the outlier is omitted, from 98.0 to a value of 37.4: omitting 414 reduces the standard deviation by a factor of almost three. However, the interquartile range, which is 83 for the whole data set, decreases relatively much less (to 71.25) when the outlier is omitted. This illustrates clearly that the interquartile range is a resistant measure of dispersion, while the standard deviation is not.
Which, then, should you prefer as a measure of dispersion: range, interquartile range or standard deviation? For exploring and summarising dispersion (spread) in data values, the interquartile range is safer, especially when outliers are present. For inferential calculations, which you will meet later in the course, the standard deviation is used, possibly with extreme values removed. The range should only be used as a check on calculations. Clearly the mean must lie between the smallest and largest data values, somewhere near the middle if the data are reasonably symmetric; and the standard deviation, which can never exceed the range, is usually close to about one-quarter of it.
5.8 Sample variance
It is worth noting that a special term is reserved for the square of the sample standard deviation: it is known as the sample variance.
The sample variance
The sample variance of a data sample x 1, x 2, …, xn is given by
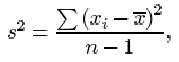
where ![]() is the sample mean.
is the sample mean.
Example 3: Calculating the variance
The variance of the eleven β endorphin concentration differences is
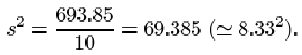
5.9 A note on accuracy
To what accuracy should you give the results of calculations? If you look through the examples in this section, you will find that, in general, results have been given either to the same accuracy as the data or rounded to one decimal place or one significant figure more than is given in the data. There is no hard and fast rule about what you should do: appropriate accuracy depends on a number of factors including the reliability of the data and the size of the data set. However, you should avoid either rounding the data too much, so that valuable information is lost, or too little, thus suggesting that your results are more accurate that can be justified from the available data.
As a rough guide, it is usually satisfactory to round a result to one significant figure more than is given in the data. But note that this rough guide applies only to results quoted at the ends of calculations: intermediate results should not be rounded. If you round a result and then use the rounded value in subsequent calculations – for instance, if you use a rounded value for the mean when calculating the standard deviation of a data set – then this sometimes leads to quite serious inaccuracies (known as rounding errors).
In Example 1, the mean was rounded to two decimal places before calculating the residuals. The squared residuals were also rounded before finding the standard deviation. This was done simply for clarity of presentation.
5.10 Symmetry and skewness
For many purposes the location and dispersion of a set of data are the main features of its distribution that we might wish to summarise, numerically or otherwise. But for some purposes it can be important to consider a slightly more subtle aspect: the symmetry, or lack of symmetry, in the data.
Example 4: Family sizes of Protestant mothers in Ontario
The following data are taken from the 1941 Canadian Census and comprise the sizes of completed families (numbers of children) born to a sample of Protestant mothers in Ontario aged 45–54 and married at age 15–19. The data are split into two groups according to how many years of formal education the mothers had received.
| Mother educated for six years or less |
| 14 13 4 14 10 2 13 5 0 0 13 3 9 2 10 11 13 5 14 |
| Mother educated for seven years or more |
| 0 4 0 2 3 3 0 4 7 1 9 4 3 2 32 16 6 0 13 6 6 5 9 10 5 4 3 3 5 2 3 5 15 5 |
(Keyfitz, N. (1953) A factorial arrangement of comparisons of family size. American J. Sociology, 53, 470–480.)
Figure 21 shows a bar chart of some of the data from Table 12: it shows the numbers of children born to the 35 mothers who had at least seven years of education.
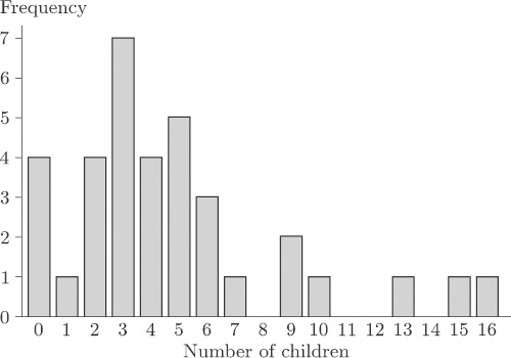
As you can see, the bar chart shows a marked lack of symmetry.
Exercise 1: Family size
For each of the two data sets in Table 12, calculate the range, the median, the upper and lower quartiles and the interquartile range.
Use the statistical functions of your calculator to find the mean, the standard deviation and the variance for each of the two data sets.
Answer
Solution
After sorting into order of increasing size, the two data sets are as follows.
| Mother educated for six years or less |
| 0 0 2 2 3 4 5 5 9 10 10 11 13 13 13 13 14 14 14 |
| Mother educated for seven years or more |
| 0 0 0 0 1 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 5 5 5 5 5 6 6 6 7 9 9 10 13 15 16 |
For the mothers with at most six years of education, the sample size n is 19. The range is just the difference between the largest and the smallest values in the sample, so it is 14−0=14. The median is
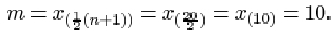
The lower quartile is
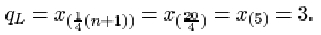
The upper quartile is
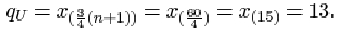
Thus the interquartile range is
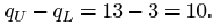
For the other data set, the sample size n is 35. The range is 16−0=16. The median is
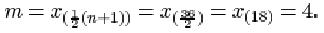
The lower quartile is
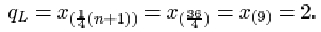
The upper quartile is
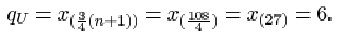
The interquartile range is
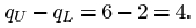
The mean and the standard deviation for the first sample are respectively 8.158 and 5.188, or approximately 8.2 and 5.2. The variance is the square of the standard deviation, 5.1882 = 26.9 (approx.). For the second sample, the mean, standard deviation and variance are respectively 4.8, 3.954 = 4.0 (approx.) and 3.9542 = 15.6 (approx.).
Detection of lack of symmetry is of considerable importance in data analysis and inference. One reason is that the most important summary measure of the data is the typical or central value in the context of which the sample median and the sample mean were introduced. When the data are roughly symmetrically distributed, all ambiguity is removed because the median and the mean will nearly coincide. However, when the data are very far from symmetrical, not only will these measures not coincide but we may even be pressed to decide whether any summary measure of this kind is appropriate. There are other reasons for the importance of symmetry in data analysis. For instance, most statistical methods involve producing a mathematical (probability) model for data, and the choice of an appropriate model may depend on whether the data are symmetrical.
Numerical data that are not symmetrical, in the sense that a bar chart or histogram shows clear lack of symmetry, are said to be skew or skewed. In Figure 21, the general pattern of lack of symmetry is that the main bulk of the data take relatively low values, towards the left of the bar chart, and to the right of the bar chart there is a relatively large ‘tail’ of relatively high values. Because of this ‘tail’ to the right, data showing this sort of pattern are said to be right-skew or positively skewed.
These data on family sizes arise from counts, so they are discrete, and a bar chart is an appropriate way to picture them. But the concept of skewness applies also to measured (continuous) data. Figure 22 shows a histogram of the time intervals (in seconds) between pulses along a nerve fibre.
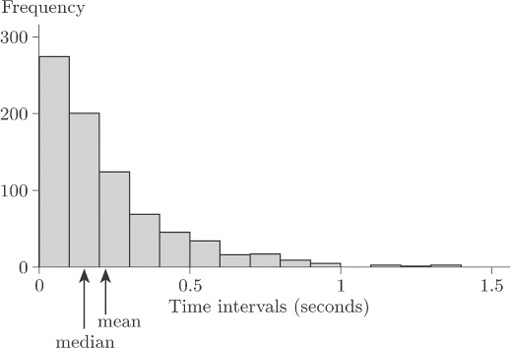
Again, the general pattern is one of lack of symmetry. The data have a relatively large ‘tail’ to the right of the diagram for relatively long time intervals, so again they are described as right-skew or positively skewed.
The mean and the median are shown in Figure 22. Notice that the mean is greater than the median; this is the case for right-skew data in general.
Clearly not all data sets that exhibit lack of symmetry are right-skew. Data sets whose bar charts or histograms look generally like the mirror images of Figures 21 and 22 are said to be left-skew or negatively skewed. In general, the mean is less than the median for left-skew data. (Note that the direction – left or right – used to describe the skewness is the direction in which the long ‘tail’ of the distribution points, not the end of the diagram where the main bulk of the data lie.) In practice, right-skew data are relatively common, and often arise (as in the data sets in Figures 21 and 22) where there is some natural lower limit on the values of a variable, so that it is impossible for there to be a long ‘tail’ to the left. In the nature of things, natural upper limits on the values of variables tend to be less common, so that left-skew data are encountered rather less frequently.
Figure 23 is a bar chart of the family sizes of the first group of mothers in Table 12, who were educated for six years or less.
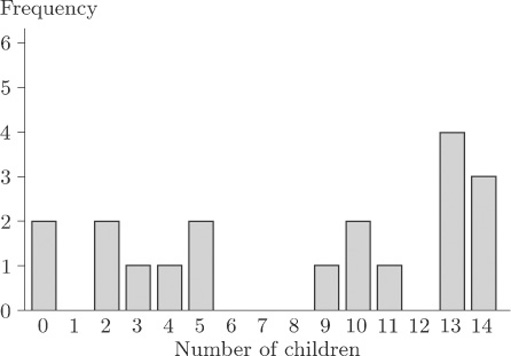
This bar chart does not exhibit such a clear lack of symmetry as does Figure 21; but it is not symmetrical. This time, however, the main concentration of the data is, if anything, towards the right of the diagram and the main ‘tail’ is to the left. These data are left-skew, or negatively skewed.
As well as a general impression of skewness obtained by looking at histograms or bar charts, a numerical measure of symmetry is both meaningful and useful.
The generally accepted measure is the sample skewness, defined as follows.
The sample skewness
The sample skewness of a data sample x 1, x 2, …, xn is given by
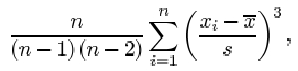
where ![]() is the sample mean and s is the sample standard deviation.
is the sample mean and s is the sample standard deviation.
Notice the term ![]() in this formula. Since
in this formula. Since ![]() is positive when
is positive when ![]() is positive and negative when
is positive and negative when ![]() is negative, observations greater than the sample mean contribute positive terms to the sum, while observations less than the sample mean contribute negative terms. Perfectly symmetric data have a skewness of 0, because the contributions from positive and negative terms cancel out. In skewed data, the sign of the sample skewness depends on the direction of the skew. For right-skew data, the bigger ‘tail’ is on the right, so that it consists (largely at any rate) of values greater than the sample mean. In other words, in right-skew data there are a lot of values much greater than the sample mean, and fewer values much less than the sample mean. The power of 3 applied to the terms in the sum, in the formula for sample skewness, means that values a long way from the mean contribute a disproportionately large amount to the sum. Thus, in right-skew data, the positive terms in the sum outweigh the negative terms, and the sample skewness comes out to be positive. In left-skew data, it is the other way round and the sample skewness is negative. (This, in a sense, is the reason why right-skew data are also said to be positively skewed, and left-skew data are negatively skewed.) The data of Figure 21 have a sample skewness of 1.36, and those in Figure 23 have a sample skewness of −0.33. That is, the data for the group of mothers with seven or more years of education have positive skewness, while for the group of mothers with six or less years of education, the sample skewness is negative. The asymmetry is rather slight for the second group of mothers, certainly by comparison to the first group of mothers.
is negative, observations greater than the sample mean contribute positive terms to the sum, while observations less than the sample mean contribute negative terms. Perfectly symmetric data have a skewness of 0, because the contributions from positive and negative terms cancel out. In skewed data, the sign of the sample skewness depends on the direction of the skew. For right-skew data, the bigger ‘tail’ is on the right, so that it consists (largely at any rate) of values greater than the sample mean. In other words, in right-skew data there are a lot of values much greater than the sample mean, and fewer values much less than the sample mean. The power of 3 applied to the terms in the sum, in the formula for sample skewness, means that values a long way from the mean contribute a disproportionately large amount to the sum. Thus, in right-skew data, the positive terms in the sum outweigh the negative terms, and the sample skewness comes out to be positive. In left-skew data, it is the other way round and the sample skewness is negative. (This, in a sense, is the reason why right-skew data are also said to be positively skewed, and left-skew data are negatively skewed.) The data of Figure 21 have a sample skewness of 1.36, and those in Figure 23 have a sample skewness of −0.33. That is, the data for the group of mothers with seven or more years of education have positive skewness, while for the group of mothers with six or less years of education, the sample skewness is negative. The asymmetry is rather slight for the second group of mothers, certainly by comparison to the first group of mothers.
It is, of course, possible to calculate the sample skewness on a calculator, but the computations are rather tedious. In practice a statistician would use a computer — and therefore practice on calculating skewness is left to the computer book.
Exercise 2 Alcohol consumption
Table 5 contains average annual alcohol consumption figures (in 1/person) for 15 countries. The figure for France was observed to be much higher than the other figures (an apparent outlier). In order of increasing size, the other values in the data set are as follows.
| 3.1 | 3.9 | 4.2 | 5.6 | 5.7 | 5.8 | 6.6 | 7.2 | 8.3 | 9.9 | 10.8 | 10.9 | 12.3 | 15.2 |
Calculate the median, the upper and lower quartiles and the interquartile range for these alcohol consumption figures.
Answer
Solution
For these data, the sample size n is 14. The lower quartile is
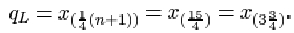
This is three-quarters of the way between x (3) =4.2 and x (4)=5.6. So
qL = 4.2 + ¾(5.6 – 4.2) = 5.25,
or approximately 5.3. The sample median is
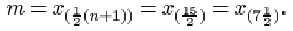
This is midway between x (6)=6.6 and x (8)=7.2, that is 6.9.
The upper quartile is
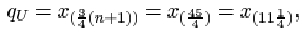
which is one-quarter of the way between x (11)=10.8 and x (12)=10.9. So
qU = 10.8 + ¼(10.9 – 10.8) = 10.825,
or approximately 10.8. The interquartile range is
qU – qL = 10.825 – 5.25 = 5.575,
or approximately 5.6.
5.11 Numerical summaries: summary
In this section, various ways of summarising certain aspects of a data set by a single number have been discussed. You have been introduced to two pairs of statistics for assessing location and dispersion. The median and interquartile range provide one pair of statistics, and the mean and standard deviation the other, each pair doing a similar job. As for the choice of which pair to use, there are pros and cons for either. You have seen that the median is a more resistant measure of location than is the mean, in the sense that its value is less affected by the presence of one or two outliers in the data. In the same sense, the interquartile range is a more resistant measure of dispersion than is the standard deviation.
The (sample) median is the central value in a data set after the data values have been sorted into order of increasing size. The lower and upper (sample) quartiles are the values that divide the data set into quarters. Denoting by x (p) the pth value in the ordered data set of n values, the median to, the lower quartile qL and the upper quartile qU are given by
m = x (½(n+1)), qL = x (¼(n+1)), qU = x (¾(n+1)).
In each case, if the subscript is not a whole number, it is interpreted by interpolating between sample values. The interquartile range is q U −q L . A much less commonly used measure of dispersion is the range, which is simply the difference between the largest and smallest values in the sample.
No sorting of the data is required when calculating the (sample) mean and (sample) standard deviation. The mean x and the standard deviation s of a sample x 1, x 2,… x 1 are given by
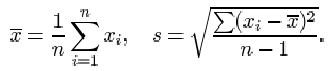
The variance is the square of the standard deviation.
The term ‘mode’ can be used to describe a ‘representative value’ in a data set; it describes the most frequently occurring observation. For numerical data, this definition needs to be modified; a mode is taken to be a clear peak in a histogram of the data. Some data sets have only one such peak and are called unimodal, others have two peaks (bimodal) or more (trimodal, multimodal).
Finally, you have learned to distinguish between data sets that are symmetrical, right-skew (or positively skewed, with a long tail of high values) and left-skew (or negatively skewed, with a long tail of low values). The sample skewness is a numerical summary of the skewness of a data set.
6 Conclusion
In this course, you have been introduced to a number of ways of representing data graphically and of summarizing data numerically. We began by looking at some data sets and considering informally the kinds of questions they might be used to answer.
An important first stage in any assessment of a collection of data, preceding any numerical analysis, is to represent the data, if possible, in some informative diagrammatic way. Useful graphical representations that you have met in this course include pie charts, bar charts, histograms and scatterplots. Pie charts and bar charts are generally used with categorical data, or with numerical data that are discrete (counted rather than measured). Histograms are generally used with continuous (measured) data, and scatterplots are used to investigate the relationship between two numerical variables (which are often continuous but may be discrete). You have seen that a transformation may be useful to aid the representation of data.
However, most diagrammatic representations have some disadvantages. In particular, pie charts are hard to assess unless the data set is simple, with a restricted number of categories. Histograms need a reasonably large data set. They are also sensitive to the choice of cutpoints and the widths of the classes.
Numerical summaries of data are very important. You have been introduced to two main pairs of statistics for assessing location and dispersion. The principal measures of location that have been discussed are the mean and the median, and the principal measures of dispersion are the interquartile range and the standard deviation (together with a related measure, the variance). Because of the way they are calculated, these measures ‘go together’ in pairs – the median with the interquartile range, the mean with the standard deviation. The median and interquartile range are more resistant than are the mean and standard deviation; that is, they are less affected by one or two unusual values in a data set.
The mode has also been introduced. The term ‘mode’ is used for the most frequently occurring value in a set of categorical data, as well as to describe a clear peak in the histogram of a set of continuous data.
You have learned about the terms used to describe lack of symmetry in a data set. A data set is said to be right-skew or positively skewed if a histogram (or bar chart, for numerical discrete data) has a relatively large and long tail towards the higher values, on the right of the diagram. The terms left-skew and negatively skewed are used when there is a relatively long tail towards the lower values, on the left of the diagram. Note that the direction of the tail, and not the direction of the main concentration of the data values, is used to describe the skewness. The sample skewness, which is a numerical summary measure of skewness, has also been defined.
Acknowledgements
All materials included in this course are derived from content originated at the Open University.
Course image: Kjetil Korslien in Flickr made available under Creative Commons Attribution-NonCommercial 2.0 Licence.
Except for third party materials and otherwise stated (see terms and conditions), this content is made available under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Licence
Don't miss out:
If reading this text has inspired you to learn more, you may be interested in joining the millions of people who discover our free learning resources and qualifications by visiting The Open University - www.open.edu/ openlearn/ free-courses
Copyright © 2016 The Open University