Squares, roots and powers
Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Friday, 19 April 2024, 5:52 PM
Squares, roots and powers
Introduction
This free course, Squares, roots and powers, reminds you about powers of numbers, such as squares and square roots. In particular, powers of 10 are used to express large and small numbers in a convenient form, known as scientific notation, which is used by scientific calculators.
This OpenLearn course provides a sample of level 1 study in Mathematics.
Learning outcomes
After studying this course, you should be able to:
evaluate the squares, cubes and other powers of positive and negative numbers with or without your calculator
estimate square roots and calculate them using your calculator
describe the power notation for expressing numbers
use your calculator to find powers of numbers
multiply and divide powers of the same number.
1 Squares, cubes and roots
1.1 Squares
In general, to square a number, multiply it by itself. This is denoted by writing a small ‘2’ to the top right of the number,
e.g. 4 squared, written 42, is 4 × 4 = 16.
Example 1
A gardener is planning to create a square patio using square concrete slabs. A row of 11 large slabs just fits across the width of the areas she wants to cover.
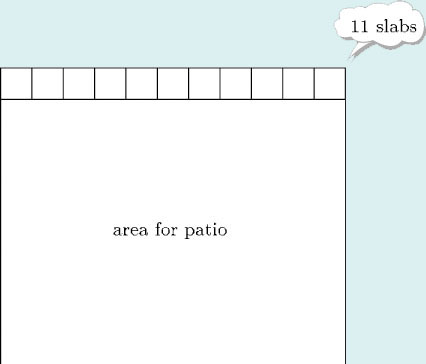
(a) How many rows of slabs will she use?
(b) How many slabs will she need altogether?
(c) The slabs are 0.75 m square. What area will the patio be?
Answer
(a) Since the patio is square and it is 11 slabs wide, it must be 11 slabs long too, so there are 11 rows of slabs.
(b) That means that altogether she will need 11 × 11, or 112 = 121 slabs.
(c) There are several ways of finding the area of the patio. One method is to say that each slab is 0.75 m by 0.75 m, which is an area of 0.752 square metres. So the patio is 112 × 0.752 square metres. Using a calculator gives 68.0625 square metres. An alternative method is to say that each side of the patio is 11 × 0.75 m. so the area of the patio is (11 × 0.75)2 square metres. Using a calculator again gives 68.0625 square metres. (Notice (11 × 0.75)2 = 112 × 0.752.)
So the patio will be just over 68 square metres.
Example 2
In an art course the teacher plans to asks each of the pupils to draw a sketch of every child in the class, including a self-portrait, on separate sheets of paper. There are 26 children in the class. Find an upper estimate for the number of sheets of drawing paper he should supply for the whole class. Find a lower estimate. Use your calculator to find the exact number of sheets of paper.
Answer
Each of the 26 children will need 26 pieces of paper, so altogether 26 × 26, i.e. 262 sheets of paper are required.
Upper estimate: If there were 30 pupils in the class he would need 30 × 30 = 900 sheets of paper.
Lower estimate: If there were only 20 pupils the teacher would need 202 = 400 sheets of paper.
So he will need something in between 400 and 900.
On the calculator, 262 = 676.
This is in reasonable agreement with the rough check, so 676 sheets of paper are required. (He would probably take 700 to have spares.)
1.1.1 Try some yourself
Activity 1
Evaluate the following:
(a) 62
(b) 0.52
(c) 1.52
Answer
(a) 62 = 6 × 6 = 36
(b) 0.52 = 0.5 × 0.5 = 0.25
(c) 1.52 = 1.5 × 1.5 = 2.25
Activity 2
Square carpet tiles measure 50 cm by 50 cm (or 0.5 m by 0.5 m).
(a) What area is covered by one tile? Give your answer (i) in square centimetres (cm2) and (ii) in square metres (m2).
(b) What area, in m2, will 100 tiles cover?
(c) How many tiles are needed to cover 1 square metre?
(d) How many tiles are needed to cover a room with an area of 16 m2?
(e) If the room in (d) is square, how many tiles go along each edge?
Answer
(a)(i) One tile covers 50 × 50 = 2500 cm2.
(a)(ii) To convert this to m2, you could divide by 1002 to give
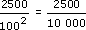= 0.25 m2.Alternatively (and more simply) convert first: each tile measures
0.5 m × 0.5 m and so has an area 0.5 m × 0.5 m = 0.25 m2.
(b) One tile covers 0.25 m2 so 100 tiles cover 100 × 0.25 = 25 m2.
(c) Since each tile covers 0.25 m2, 4 tiles will cover 4 × 0.25 = 1 m2.
(d) 4 tiles cover 1 m2 so 16 × 4 = 64 tiles cover 16 m2.
(e) If the room is square and the area is 16 m2 then each edge must be 4 m, since 4 × 4 = 16 (or
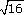=4). So 8 tiles go along each edge. (You could also have deduced this from your answer to (d), since 64 tiles is 8 × 8 tiles.)
1.2 Squaring fractions and negative numbers
You have now seen how to find squares of whole numbers and decimals. What about fractions? The rule is as before: to square a fraction, just multiply it by itself.
For example:
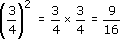
In Example 1, you could have used 
instead of 0.75. Check on your calculator that 0.752 = 
. Both answers should be 0.5625.
There may be contexts where you need to square negative numbers. Take care when doing so. Use the brackets if in doubt. Calculating by hand gives, for example:
(−9)2 = −9 × −9 = 81
However, keying in −9 and then squaring will give −81 on many scientific and graphics calculators. Why? They calculate exactly what you have asked for, i.e. −92. Since 92 is 81, −92 is −81. The number 9 is squared first, to give 81, and then made negative, to give −81. Brackets are needed to tell the calculator to make the 9 negative and then square:
(−9)2 = 81,
but without brackets −92 often means −(92).
To avoid any ambiguity, it is always best to use brackets when squaring negative numbers.
1.2.1 Try some yourself
Activity 3
Without using your calculator, find the following:
(a) 102
(b) 1002
(c) 0.12
(d) 0.012
(e)
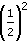
(f) (−3)2
(g) (−1)2
Answer
(a) 102 = 10 × 10 = 100
(b) 1002 = 100 × 100 = 10 000
(c) 0.12 = 0.1 × 0.1 =
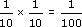= 0.01(d) 0.012 = 0.01 × 0.01 =
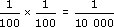
= 0.0001
(e)
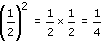
(f) (−3)2 = −3 × −3 = 9
(g) (−1)2 = −1 × −1 = 1
Activity 4
Explain why brackets should be used when writing the expression (−1)2.
Answer
If you write −12 it is not clear whether you mean to square 1 first then make the answer negative, giving −1, or to square −1, giving 1. Many calculators would assume you meant −(1)2, and return the answer −1.
Activity 5
Use your calculator to find the following, using your answers to the appropriate parts of Question 1 as estimates.
(a) 962
(b) 10.652
Answer
(a) Rough check: 1002 = 10 000.
Calculator gives 962 = 9216.
(b) Rough check: 102 = 100.
Calculator gives 10.652 = 113.4225.
1.3 Square roots
Given any number, you now know how to find its square. But, given the squared number, how do you find the original number?
Example 3
If the gardener in Example 1 had only 49 paving slabs, what size of square patio could she make?
Answer
You probably spotted that 49 is 7 × 7, or 72, so she could make a square patio 7 slabs by 7 slabs.
Since 72 = 49, 7 is the square root of 49, written
7 =
.
Sometimes you can just look at a number and spot its square root, if the number is a ‘perfect square’ (i.e. the result of squaring a whole number). For example, 25 is a perfect square, and 
= 5. But more often than not you will need to use your calculator for square roots, and it is important to be able to find rough estimates as a check on your calculator work. So if you wanted 
, you would know that it would lie between = 7 and 
= 8, and you would expect an answer of seven point something. (It is 7.416 …).
Technically, −7 is also a square root of 49, since (−7)2 = 49. This is called the negative square root. The sign √ is customarily used to denote the positive square root, so = 7 and − = −7.
In Example 3, only the positive square root is relevant (patios have positive length sides).
Example 4
The owners of a new house, with a bare earth garden, see an advertisement for 44 square metres of turf, ‘free to a good home – only pay transportation’. They were planning a square lawn surrounded by flower beds.
Find a rough estimate for the square root of 44. Use your calculator to find 
and find the size of the square lawn which the turf would make.
Answer
Rounding 44 down to 40 doesn't help – you don't know the square root of 40 either! But you do know that 62 = 36 (which is less than 44) and 72 = 49 (which is greater than 44) so lies between 6 and 7. You could leave the answer as ‘between 6 and 7’ or guess it as 6.5, say. The calculated answer is 6.6332 (rounded to four decimal places). So the turf would make a lawn about 6.6 m square.
1.3.1 Try some yourself
Activity 6
The new home owners from Example 4 above want to price grass seed, as well as the turf (transport only). The best buy seems to be loose seed, which says ‘1 kilo covers 80 m2’. They wonder what length the side of an 80 m2 square lawn would be? Make an estimate and then use your calculator to find 
and hence the side of the square lawn.
Answer
A square of side 9 m has an area of 81 m2. So 80 m2 would be a little less than this.
= 8.94.... So the length of the side of the square lawn would be 8.9 m.
Activity 7
Use your calculator to find each of the following, estimating the answer first in each case.
(a)
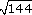
(b)
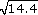
(c)
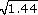
(d)
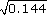
Where necessary, round your answers to four decimal places.
Answer
(a) Since 12 × 12 = 144, the answer must be
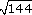= 12. The calculator confirms this.(b) Since 32 = 9 and 42 = 16,
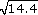must lie between 3 and 4.Calculator gives
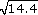
3.7947 rounded to four decimal places.(c) Since 12 = 1 and 22 = 4,
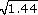must lie between 1 and 2.Calculator gives
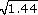= 1.2.(d) Since 0.32 = 0.09 and 0.42 = 0.16,
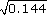must lie between 0.3 and 0.4.Looking at the pattern of parts (a) and (c), and since
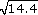= 3.7947, a good guess would be that 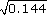= 0.3795 rounded to four decimal places.Indeed, the calculator gives
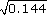
0.3795 rounded to four decimal places.
1.4 Cubes
To find the cube of a number, multiply three copies of it together. For example:
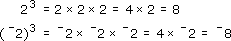
You can use your calculator to find cubes. 23 is ‘two cubed’ or ‘two to the power three’. Just as ‘square root’ is the opposite process to squaring, so 'cube root' is the opposite process to cubing.
43 = 64, so 
= 4.
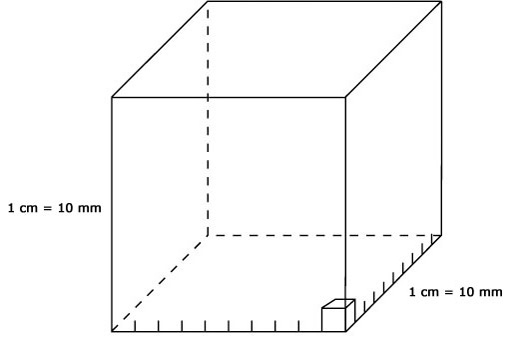
In the same way that square units are used to measure area, cubic units are used to measure volume. A cube measuring 1 cm × 1 cm × 1 cm has a volume of 1 centimetre cubed, or 1 cubic centimetre, written as 1 cm3, or 1 cc. The volume of a ‘box’ is length x width x height, so the volume of this cube (10 mm × 10 mm × 10 mm) in millimetres is
1 cm3 = 10 mm × 10 mm × 10 mm = 1000 mm3.
Example 5
My half-litre measuring jug is marked off in divisions of 100 ml, with subdivisions of 20 ml. I want to measure out 420 cc, but the only conversion table I have tells me that a litre is one cubic decimetre. (One decimetre is a tenth of a metre.) How many cubic centimetres are there in a litre? Can I use the measuring jug for 420 cc?
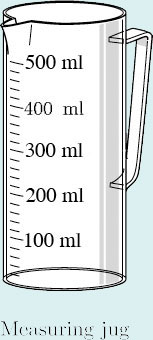
Answer
There is one cubic decimetre in a litre, so 1 litre measures 1 dm × 1 dm × 1 dm (if shaped into a cube). (Note: 1 m = 10 dm = 100 cm.) There are 10 centimetres in a decimetre, so a 1 litre cube would measure
10 cm × 10 cm × 10 cm = 1000 cm3.
So 1 litre is 1000 cm3. This is a useful result.
But there are 1000 millilitres in a litre, so it turns out that a millilitre is the same as a cubic centimetre.
1 ml = 1 cm3.
So I can use the jug to measure 420 ml, or 420 cc (or cm3).
(Note: 1 cubic centimetre can be written as 1 cc or 1 cm3.)
1.4.1 Try some yourself
Activity 8
If a litre is one cubic decimetre, how many litres are there in a cubic metre?
Answer
Since a litre is one cubic decimeter, the question is asking how may cubic decimetres are in a cubic metre.
1 metre = 10 decimetres
so 1 m3 = 103 cubic decimetres.
Hence there are 1000 litres in a cubic metre.
Activity 9
Find the following without using your calculator, as an estimate for the calculator work in the next question.
(a) (−1)3
(b) 33
(c) 1003
(d) 0.13
Answer
(a) (−1)3 = −1 × −1 × −1 = 1 × −1 = −1
(b) 33 = 3 × 3 × 3 = 9 × 3 = 27
(c) 1003 = 100 × 100 × 100 = 10 000 × 100 = 1000 000 (a million)
(d)
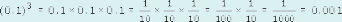
Activity 10
Use your calculator to find the following.
(a) (−1.2)3
(b) 3.33
(c) 1013
(d) 0.1213
Answer
(a) Estimate: (−1)3 = −1.
Calculate: (−1.2)3 = −1.728.
(b) Estimate: 33 = 27.
Calculate: 3.33 = 35.937.
(c) Estimate: 1003 = 1000 000.
Calculate: 1013 = 1030 301.
(d) Estimate: .13 = .001.
Calculate: 0.1213 = 0.00177 (3 s.f.)
Activity 11
What are the following?
(a)
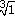
(b)
Answer
(a)
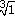= 1 since 13 = 1.(b)
= 10 since 103 = 1000.
Activity 12
Find the volume of a one-foot cube in cubic metres (1 foot = 30.48 cm). Estimate your answer first. Round your answer to three decimal places.
Answer
To estimate an answer, choose a simple approximation, say
1 foot 30 cm = 0.3 m.
Then 1 foot cubed (0.3)3 = 0.027 m3.
More accurately, 1 foot = 30.48 cm = 0.3048 m.
So 1 foot cubed = (0.3048)3 = 0.028 m3 to three d.p.
Activity 13
Without using your calculator, find the following, as estimates for the calculator work in Question 7.
(a) 92
(b) 43
(c)
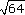
(d)
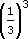
(e) (−3)2
Answer
(a) 92 = 9 × 9 = 81
(b) 43 = 4 × 4 × 4 = 16 × 4 = 64
(c)
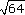= 8 (since 82 = 64)(d)
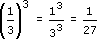
(e) (−3)2 = −3 × −3 = 9
Activity 14
Use your calculator to find:
(a) 9.422
(b) 3.653
(c)
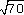
(d) 0.333
(e) (−2.713)2
Use your answers to the previous question as rough checks. Round your answers to four decimal places.
Answer
(a) 9.422 = 88.7364
(b) 3.653
48.6271(c)
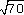
8.3666(d) 0.333
0.0359 (check this by calculating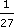 
, the estimate from 3(d) above, as a decimal.(e) (−2.713)2
7.3604 (N.B. To get this answer on a calculator, remember the brackets.)
2 Powers
2.1 The impact of a power
Here is a tale based on an ancient Eastern legend, which gives an idea of the impact of raising a number to a power.
Example 6
A long time ago there lived a very rich king whose son's life was saved by a poor old beggar woman. The king was naturally very grateful to the woman, so he offered to give her anything that she wanted. Much to the king's surprise the old lady just asked for two bags of rice. When asked why she specifically wanted the rice, she explained that she would like to have her son to stay and that if she had some rice she would be able to feed him. The king felt that this was far too small a reward so he asked if there were any other members of her family that she might like to have to stay. She replied that she would like to have her two daughters the following week, so four bags of rice then would be a great help. The king agreed to this and suggested that she might like to think of having more of her family to stay. He said he would be prepared to double the number of bags he gave her each week. At this point his accountant got very agitated and asked him to consider very carefully what he was offering! What was he worried about?
Answer
In order to decide if the king was being exceptionally generous, you need to look at exactly what he was proposing. In the beginning the numbers are quite small, 2 bags of rice in the first week, 4 bags in the second, then 8 in the third, 16 in the fourth, 32 in the fifth and so on.
Week 1: 2 bags of rice = 2
Week 2: 2 × 2 bags of rice = 4
Week 3: 2 × 2 × 2 bags of rice = 8
Week 4: 2 × 2 × 2 × 2 bags of rice = 16
Week 5: 2 × 2 × 2 × 2 × 2 bags of rice = 32
However, to get a feel for how the numbers are growing, look at them in another way.
It is not particularly convenient to write out all these 2s, particularly if you want to go on and look at the situation in week 52, say, i.e. a year later. However, there is a short and neater way of expressing these numbers.
You can write 2 × 2 = 22 = 4 and 2 × 2 × 2 = 23 = 8.
In a similar manner, in week 4 you can write 2 × 2 × 2 × 2 = 24 = 16, … and in week 10, when there are ten twos multiplied together, you can write 210. Sometimes you may find it written 2 ^ 10 (^ is the ‘power of’ sign).
In week 1, when the number of bags is just 2, you can write this as 21.
These numbers can be worked out on your calculator. Check each of 24, 25 and 210 using your calculator.
You should find that 210 = 1024 and so see what the accountant was worried about.
2.1.1 Try some yourself
Activity 15
The size of a population of micro-organisms doubles every hour. If there are two of these creatures to start with, how many will there be after five hours?
Answer
After one hour there are 2 × 2 = 4 micro-organisms.
After two hours there are 2 × 4 = 8, or 2 × 2 × 2 = 23.
After five hours there are 2 × 32 = 64, or 2 × 2 × 2 × 2 × 2 × 2 = 26.
So there will be 26 = 64 after five hours.
(Note: if you gave 32 as your answer, maybe you forgot that there were 2 organisms to start with.)
2.2 Power notation
The notation in Example 6 is called power notation, or index notation. In a number such as 25, the 5 is called the power, or index, of the number.
The squares are particular examples of powers: 92, for example, can be thought of as ‘9 to the power 2’.
For most numbers, calculating powers by hand soon becomes tedious: while you might be quite happy to find 25 or 92, it would take a long and fairly dull time to find 250 or 920 by hand. So you will be using your calculator for most calculations involving powers, even when the numbers themselves are quite simple. However, there is one number whose powers are quite easy to find, namely 10. For example:
one hundred = 10 × 10 = 102 = 100;
one thousand = 10 × 10 × 10 = 103 = 1000;
one million = 10 × 10 × 10 × 10 × 10 × 10 = 106 = 1000 000.
In the same way that 2 can be written as 21 so 10 can be written as 101.
It is also easy to find powers of 1 and 0. 1 × 1 × 1 × … = 1 and 0 × 0 × 0 = 0.
Example 7
The headings on the place value tables in the OpenLearn course Numbers, units and arithmetic are tens, hundreds, thousands etc. … Write these as powers of ten. What do you think the units columns heading would be as a power of ten?
Answer
| ten | = 10 = 101 |
| hundred | = 100 = 102 |
| thousand | = 1000 = 103 |
| ten thousand | = 10 000 = 104 |
| hundred thousands | = 100 000 = 105 |
| million | = 1000 000 = 106 |
The power of ten increases for each column. So to be consistent, the units column should be 100. Putting 100 into a calculator gives 100 = 1. So the units column is 1 = 100.
2.2.1 Try some yourself
Activity 16
Find the following powers by hand, as estimates for calculator work.
(a) 107
(b) 108
(c) 34
(d) (−2)2
(e) (−2)3
Answer
(a) 107 = 10 000 000
(b) 108 = 100 000 000
(c) 34 = 3 × 3 × 3 × 3 = 27 × 3 = 81
(d) (−2)2 = −2 × −2 = 4
(e) (−2)3 = 4 × −2 = −8
Activity 17
Use your calculator to find the following and use your answers to the previous question as a check. Give your answers correct to 3 significant figures.
(a) 117
(b) 10.88
(c) 3.144
(d) (−2.2)2
(e) (−2.01)3
Answer
(a) 117 = 19 487 171
19 500 000 (3 s.f.)(b) 10.88 = 185 093 021
185 000 000 (3 s.f.)(c) 3.144 = 97.21171216
97.2 (3 s.f.)(d) (−2.2)2 = 4.84
(e) −(2.01)3 = −8.120601
−8.12 (3 s.f.)
Activity 18
(a) How many zeros are there in 1012 when written out in full? Work out a rule for finding the number of zeros in any positive whole number power of 10.
(b) Your answers to parts (d) and (e) of Question 1 may have suggested a rule for powers of negative numbers, depending on whether the power is odd or even. What is the rule?
Answer
(a) There are 12 zeros in 1012. The number of zeros for a positive power of 10 is the same as the power.
(b) An odd power of a negative number is negative. An even power of a negative number is positive.
Activity 19
Hamsters of a particular kind, left to breed in a suitable environment, double their population every month. If a friend of yours, who is thinking of breeding these hamsters, started with one pair (male and female), what population might she expect in a year's time (assuming she keeps them all)?
Answer
After 0 months (i.e. at the start) there are 2 hamsters = 2
After 1 month there are 2 × 2 hamsters, i.e. 22 = 4
After 2 months there are 2 × 2 × 2 hamsters, i.e. 23 = 8
So after 12 months there are 213 = 8192 hamsters.
Activity 20
A ploughed field has been left abandoned. It has one weed in the middle. The weed is an annual plant and its flower produces about 1000 seeds. If a tenth of these seeds germinate to produce one flower each in a year's time, estimate the possible number of dandelion flowers in the field if it is abandoned for five years. (You can assume that no other factors affect the growth of the weeds during this time).
Answer
of 1000 = 100
So 100 seeds per flower germinate each year.
At 0 years there is 1 weed.
After 1 year there are 1 × 100 = 100 weeds (which can be written as 1001).
After 2 years there are
100 × 100 = 1002 = 10 000 weeds.
So after 5 years an estimate is
1005 = 10 000 000 000 weeds (or 10 billion).
Activity 21
Cells in a laboratory culture divide into two every day, given sufficient nutrient. If there were five cells on day one, how many would there be on day ten?
Answer
On day 1 there are 5 cells
On day 2 there are 5 × 2 = 10 cells
On day 3 there are 5 × 2 × 2 = 5 × 22 = 20 cells
On day 4 there are 5 × 2 × 2 × 2 = 5 × 23 = 40 cells.
So on day 10 there are 5 × 29 = 5 × 512 = 2560 cells.
2.3 Multiplying powers
Powers of ten can be used to investigate what happens when two powers of the same number are multiplied together. For example, consider multiplying 10 by 100:
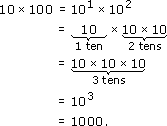
A billion is a thousand million. In terms of powers this is:
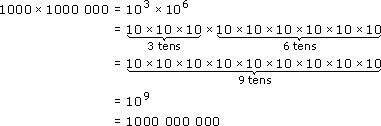
so a billion is 109 or 1000 000 000.
(An American billion is a thousand million. In UK a billion used to be a million million, but now the American billion is the standard usage.)
Note: The number of zeros in the whole number power of ten is the same as the power.
In the above calculations, 101 × 102 = 103 and 103 × 106 = 109, and the way these have been worked out shows that, when you multiply numbers expressed as powers of ten, you add the powers.
Powers of 10 were used because they are easy to work with, but you can just as easily show that multiplying powers of the same number always means adding the powers. For example:
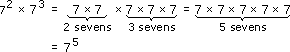
so 72 × 73 = 72+3 = 75. Check this on your calculator!
To multiply two powers of the same number, add the powers.
2.3.1 Try some yourself
Activity 22
Write the following as one number to a single power:
(a) 23 × 24
(b) 32 × 34
(c) 42 × 43 × 44
Answer
(a) 23 × 24 = 2(3 + 4) = 27
(b) 32 × 34 = 3(2 + 4) = 36
(c) 42 × 43 × 44 = 4(2 + 3 + 4) = 49
Activity 23
Without using your calculator, find the following, as estimates for calculation work in the next question.
(a) (−1)5
(b) 34
Answer
(a) (−1)5 = −1 (any odd power of −1 is −1)
(b) 34 = 3 × 3 × 3 × 3 = 81
Activity 24
Use your calculator to find the following.
(a) (−1.3)5
(b) 3.24
(Use your answers to the previous question as rough checks.) Round your answers to four decimal places.
Answer
(a) (−1.3)5
−3.7129(b) 3.24 = 104.8576
2.4 Dividing powers
Now consider division in the same way. For example:
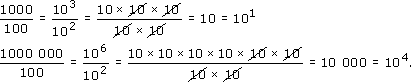
So 103 ÷ 102 = 101 and 106 ÷ 102 = 104, which suggests that dividing the powers of ten means subtracting the powers. You can see that the two tens underneath have cancelled with two of the tens on top in each case, which shows why the number of tens underneath is subtracted from the number on top. This argument applies equally well to any number. For example:
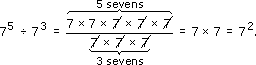
Work out 75 ÷ 73 on your calculator to check this.
To divide two powers of the same number, subtract the powers.
2.4.1 Try some yourself
Activity 25
Write the following as a number to a single power:
(a) 26 ÷ 22
(b) 1010 ÷ 107
(c) 78 ÷ 74
Answer
(a) 26 ÷ 22 = 2(6 − 2) = 24
(b) 1010 ÷ 107 = 10(10 − 7) = 103
(c) 78 ÷ 74 = 7(8 − 4) = 74
Activity 26
Express as powers of ten
(a) a million
(b) a thousand
(c) a million divided by a thousand
Answer
(a) a million = 1 000 000 = 106
(b) a thousand = 1 000 = 103
(c) 106 divided by 103 = 106–3 = 103 = a thousand
2.5 The power zero
Now, what happens if you divide a number by itself? You should get the answer 1. For example
so 100 must equal 1. This must be true for any number (except for 0, because there is a problem in defining 00). So, for example, 70 = 1, 1230 = 1, 10000 = 1. It even works for negative and decimal numbers. Check a few numbers on your calculator to see that raising to the power 0 gives 1.
Any non-zero number raised to the power 0 is 1.
2.5.1 Try some yourself
Activity 27
What are the following?
(a) 10
(b) 01
(c) 20
(d) 02
Answer
(a) 10 = 1
(b) 01 = 0
(c) 20 = 1
(d) 02 = 0 × 0 = 0
2.6 Negative powers
Now look at what happens when the power is negative. What does 10−3 mean? What is the result of the following calculation?
100 ÷ 100 000
What you are actually being asked to find is:
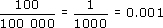
But look at the calculation again. Using the rule for the division of powers of numbers gives:
102 ÷ 105 = 102−5 = 10−3
So 10−3 = 0.001. But you can also write this result as:
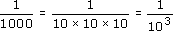
This means that 10−3 can be thought of as 1 divided by 103.
This result is true for all negative powers, not just powers of ten. For example:
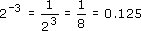
One over any number is called the reciprocal of the number.
For example, the reciprocal of 10 is 
= 10−1 and the reciprocal of 100 is 
= 
= 10−2
A number raised to a negative power is the reciprocal of the number raised to the corresponding positive power.
So 10−5 = 
= 0.00001.
Example 8
The decimal place value table columns are headed tenths, hundredths, thousandths etc. Write these as powers of ten.
Answer
a tenth = =10−1
a hundredth = = 10−2
a thousandth = 
= 10−3
So the headings of the place value table are all powers of ten. To the left of the units they are positive powers, the units column is 100, and to the right the column headings are negative powers of ten.
Notice that
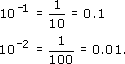
The negative power indicates the position of the decimal point — how many times it has moved to the left from 100 = 1.
10−1 = 0.1 (move one to the left); 10−2 = 0.01 (move 2 to the left) etc.
2.6.1 Try some yourself
Activity 28
Find each of the following by hand, giving your answers both as a power of ten and as a decimal number. You will use these answers as a check on your calculator work in the next question.
(a) 10−2
(b) 102 × 103
(c) 107 ÷ 104
(d) 104 ÷ 107
(e) 2−2
Answer
(a) 10−2 = 0.01
(b) 102 × 103 = 102 + 3 = 105 = 100 000
(c) 107 ÷ 104 = 107 − 4 = 103 = 1000
(d) 104 ÷ 107 = 104 − 7 = 10–3 =
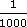= 0.001(e) 2−2 =
= 
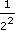(=0.25)
Activity 29
Evaluate the following, using your calculator and your answers from Question 1 as estimates.
(a) 10.3−2 (to four significant figures)
(b) 10.12 × 10.113 (to four significant figures)
(c) 10.1127 ÷ 10.214 (to one decimal place)
(d) 10.124 ÷ 10.3517 (to three significant figures)
(e) 2.2−2
Answer
Using Question 1 as a rough check, the calculator gives:
(a) 10.3−2 = 0.009 426 (to 4 s.f.)
(b) 10.12 × 10.113 = 105 400 (to 4 s.f.)
(c) 10.1127 ÷ 10.214 = 994.8 (to 1 d.p.)
(d) 10.124 ÷ 10.3517 = 0.000824 (to 3 s.f.)
(e) 2.2−2
0.2066
It is a good idea to get in the habit of estimating your answers, even if not specifically asked to do so.
Activity 30
Find each of the following by hand.
(a) 10240
(b) 10241
(c) 5−1
(d) 10−4
Answer
(a) 10240 = 1
(b) 10241 = 1024
(c)
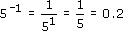
(d)
Activity 31
How many zeros are there after the decimal point in the number 10−6? How many zeros are there after the decimal point for any given negative power of 10?
Answer
10−6 = 0.000 001; there are five zeros after the decimal point. For any given negative power of 10, say 10−(NUMBER) there is one fewer zero than NUMBER. This works for 10−1, too, since 10−1 = 0.1, which has no zeros after the decimal point, i.e. one fewer than 1.
Activity 32
Try to answer the following questions
(a) Explain why a negative power of a number is one divided by the corresponding positive power of that number. (Hint: remember that a number to the power zero is 1.)
(b) Use the power button on your calculator to find the following.
(i)
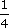
(ii)
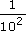
Answer
(a) Take an example, which makes the explanation easier than describing it in the abstract. Consider 10−6. Now −6 is just the same as 0 − 6, so 10−6 = 100−6. Using the rule for dividing powers, 100−6 = 100 ÷ 106. But 100 = 1. So 10−6 = 1 ÷ 106. This argument would apply equally well to any number, since any number to the power 0 is 1. (Alternatively you may have started from the other end, for example, by showing that
= 
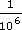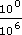= 100−6 = 10−6.)(b)
3 Scientific notation
3.1 Expressing numbers in scientific notation
Earlier you looked at place values for numbers, and why they were called powers of ten.
| Place value | 10 000 | 1000 | 100 | 10 | 1 | 0.1 | 0.01 | 0.001 | 0.0001 | 0.000 01 |
| Power of ten | 104 | 103 | 102 | 101 | 100 | 10−1 | 10−2 | 10−3 | 10−4 | 10−5 |
Using this notation, very large numbers or small decimal numbers can be expressed in a particularly neat form. This is how scientific and graphics calculators display numbers which will not fit on the screen. This is illustrated by the following examples:
107 = 10 000 000 so 25 000 000 = 2.5 × 107
10−6 = 0.000 001 so 0.000 0025 = 2.5 × 10−6
A number expressed in this form is said to be in scientific notation. Any decimal number can be converted to scientific notation, which is
A calculator automatically uses scientific notation when the answer to a calculation is very large or very small. For example, return to our tale of the king and the bags of rice. In week 52 the woman would receive 252 bags. Calculate this on your calculator. You should get 4.503 599 627 × 1015. (This number may be displayed as 4.503 599 627 E 15.) To get a feel for how big this number is, i.e. for how many bags of rice the king would need to provide a year later, look at some other numbers in scientific notation:
Great Britain has an area of 229 850 km2.
In scientific notation, 229 850 = 2.2985 × 100 000 = 2.2985 × 105.
The distance from the Earth to the Sun is 149 600 000 km.
In scientific notation, 149 600 000 = 1.496 × 100 000 000 = 1.496 × 108.
Consider now the bags of rice calculation. 1015 is 1000 000 000 000 000. So the number of bags of rice is 4503 599 627 000 000. This is a very large number of bags of rice! The king would need to give the woman over four thousand million million bags of rice in week 52. No wonder his accountant was concerned.
As mentioned above, scientific notation is also used for very small numbers.
Try finding 
on your calculator.
You should find that the answer on your calculator is 3.125 × 10−7.
(This number may be displayed as 3.125 E −7.) This time the index is negative. This is the same as:
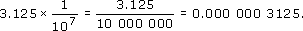
With practice you may not need the intermediate steps. You may be able to just move the decimal point the appropriate number of places (multiplying by 10−3 means moving the decimal point 3 places to the left).
5.2 × 10−3 = 0.0052
3.1.1 Try some yourself
Activity 33
Express each of the following numbers in scientific notation.
(a) Light travels 9460 700 000 000 km in a year.
(b) The average distance from the centre of the Earth to the centre of the Moon is 384 400 km.
(c) Saturn is 1427 000 000 km from the Sun.
(d) The mass of the Earth is 5976 000 000 000 000 000 000 000 kg.
(e) The Mediterranean Sea has an area of 2504 000 km2.
(f) Annapurna 1 is 8075 m high.
(g) The diameter of the Sun is 1392 000 km. Use metres in your answer.
Answer
(a) Light travels at 9.4607 × 1012 km in a year.
(b) The distance from the centre of the Earth to the centre of the Moon is 3.844 × 105 km.
(c) Saturn is 1.427 × 109 km from the Sun.
(d) The mass of the Earth is 5.976 × 1024 kg.
(e) The Mediterranean Sea has an area of 2.504 × 106 km2.
(f) Annapurna 1 is 8.075 × 103 m high.
(g) 1392 000 km is 1392 000 000 m (multiplying by 1000). In scientific notation this is
1.392 × 109 m.
(Alternatively: 1392 000 km is 1.392 × 106 km = 1.392 × 106 × 103 m = 1.392 × 109 m.)
Activity 34
The following numbers are given in scientific notation. Write each out as a single decimal number.
(a) Ben Nevis is 1.343 × 103 m high.
(b) Mercury is 5.8 × 107 km from the Sun.
(c) The distance from the Earth to the nearest star is about 4.3 × 1013 km.
(d) The Earth has a circumference of 4.0078 × 104 km at the equator.
(e) The span of the Golden Gate Bridge is 1.28 × 103 m.
(f) The Arctic Ocean has an area of 1.3986 × 107 km2.
Answer
(a) Ben Nevis is 1343 m high.
(b) Mercury is 58 000 000 km from the Sun.
(c) The distance from the Earth to the nearest star is about 43 000 000 000 000 km.
(d) The Earth has a circumference of 40 078 km at the equator.
(e) The span of the Golden Gate Bridge is 1280 m.
(f) The Arctic Ocean has an area of 13 986 000 km2.
Activity 35
Express each of the following in scientific notation.
(a) 0.53
(b) 0.0075
(c) 0.000 004
(d) 0.000 020 01
Answer
(a) 0.53 = 5.3 × 10−1
(b) 0.0075 = 7.5 × 10−3
(c) 0.000 004 = 4 × 10−6
(d) 0.000 020 01 = 2.001 × 10−5
Activity 36
Express each of the following in conventional decimal notation.
(a) 2.03 × 10−4
(b) 1.4 × 10−3
(c) 5.67 × 10−5
Answer
(a) 2.03 × 10−4 = 0.000 203
(b) 1.4 × 10−3 = 0.0014
(c) 5.67 × 10−5 = 0.000 0567
3.2 Using scientific notation
Scientific notation can be very useful when estimating the answers to calculations involving very large and/or small decimal numbers.
Example 9
A lottery winner won £7851 000. He put the money straight into a deposit account which earns 7.5% interest per annum (i.e. each year). If he wanted to live off this interest, how much per day would it be?
Answer
The amount is £7851 000 × 
÷ 365.
Estimate first to provide a check for the calculator work.
7851 000 = 7.851 × 106 8 × 106
= 7.5 × 10−2 8 × 10−2
365 = 3.65 × 102 4 × 102
So the estimate becomes:
(8 × 106) × (8 × 10−2) ÷ (4 × 102).
Now separate the digits from the powers of 10 to give:
(8 × 8 ÷ 4) × (106 × 10−2 ÷ 102).
Since 8 × 8 ÷ 4 = 16 and 106 × 10−2 ÷ 102 = 106+−2−2 = 102, the estimate is 16 × 102 = 1600 (£1600 a day!).
On a calculator, 7851 000 × 0.075 ÷ 365 gives £1613 rounded to the nearest pound, which is quite close to the estimate.
3.2.1 Try some yourself
Activity 37
Use the method outlined in Example 9 to estimate each of the following, and then use your calculator to evaluate each, giving your answers to six significant figures.
(a) 2521 ÷ 38
(b) 17.85 × 286.3
(c) 1452 ÷ 0.0072
(d) 0.0053 × 0.0078 ÷ 0.6821
(e) 0.000 923 × 0.007 67.
Answer
(a) Estimate: 2521 = 2.521 × 103
3 × 10338 = 3.8 × 101
4 × 101.So 2521 ÷ 38
= 
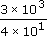× 103−1= 0.75 × 102 = 75.
Calculate: 2521 ÷ 38 = 66.3421 rounded to six significant figures.
(b) Estimate: 17.85 = 1.785 × 101
2 × 101286.3 = 2.863 × 102
3 × 102.So 17.85 × 286.3
2 × 101 × 3 × 102= 2 × 3 × 101 × 102 = 6 × 103 = 6000.
Calculate: 17.85 × 286.3 = 5110.46 rounded to six significant figures.
(c) Estimate: 1452 = 1.452 × 103
1.4 × 1030.0072 = 7.2 × 10-3
7 × 10−3.(Notice that in this case it is easier to round to 1.4 than to 1 or 1.5, anticipating the next step, since it is easier to find 1.4 ÷ 7 than 1 ÷ 7 or 1.5 ÷ 7.)
So 1452 ÷ 0.0072
= 
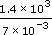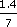× 103–−3= 0.2 × 103+3 = 0.2 × 106 = 2 × 10−1 × 106
= 2 × 10−1+6 = 2 × 105 = 200 000.
Calculate: 1452 ÷ 0.0072 = 201 667 rounded to six significant figures.
(d) Estimate: 0.0053 = 5.3 × 10−3
5 × 10−30.0078 = 7.8 × 10−3
8 × 10−30.6821 = 6.821 × 10−1
7 × 10−1.So
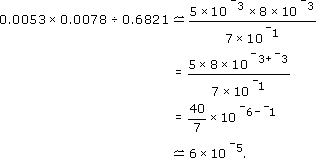
Calculate: 0.0053 × 0.0078 ÷ 0.6821
= 6.06069 × 10−5 = 0.000 060 6069 rounded to six significant figures.
(Notice that the calculator gives the answer in scientific notation.)
- (e)
0.000 923 × 0.007 67 = 9.23 × 10−4 × 7.67 × 10−3
Estimate:
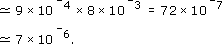
Calculate:
0.000 923 × 0.007 67 = 7.079 41 × 10−6.
Activity 38
A light year is the distance light travels through space in one year. The centre of the Milky Way galaxy is 2.6 × 104 light years away from Earth. One light year is 9.46 × 1012 km. How far away is the centre of the Milky Way in kilometers? Estimate your answer first and then use your calculator to do the calculation, giving your answer in scientific notation.
Answer
Estimate: The centre is roughly 3 × 104 light years away, and each light year is roughly 9 × 1012 km, so the distance to the centre is approximately 3 × 104 × 9 × 1012 = 27 × 1016 = 2.7 × 1017.
Calculate:
2.6 × 104 × 9.46 × 1012 = 2.4596 × 1017.
4 Open Mark quiz
Now try the quiz and see if there are any areas you need to work on.
Conclusion
This free course provided an introduction to studying Mathematics. It took you through a series of exercises designed to develop your approach to study and learning at a distance and helped to improve your confidence as an independent learner.
Acknowledgements
Except for third party materials and otherwise stated (see terms and conditions), this content is made available under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Licence
Course image: LittleDaan in Flickr made available under Creative Commons Attribution 2.0 Licence.
All written material contained within course originated at The Open University.
Don't miss out:
If reading this text has inspired you to learn more, you may be interested in joining the millions of people who discover our free learning resources and qualifications by visiting The Open University - www.open.edu/ openlearn/ free-courses