
Last November, Maine voters approved, by a slim majority, a ballot initiative to adopt a voting system called “instant runoff.”
This system has been proposed as an alternative to our traditional election method – called “plurality voting” – by several politicians, including 2016 Green Party presidential candidate Jill Stein. It has also been implemented in various municipal elections in the United States.
Many other multi-candidate election methods have been proposed. Most of them have the drawback of being complicated, and therefore are probably not politically viable. I want to suggest a method that I believe is much better than both plurality voting and instant runoff, and just as simple as instant runoff.
Plurality voting and its problems
In plurality voting, every voter names their favorite candidate, and the candidate named most often wins.
This is the only reasonable thing to do when there are only two candidates, but it becomes problematic when there are more. The problems are well-recognized. For example, if you were every voter’s second choice among five candidates, you’d be doing very well, quite possibly better than any other candidate by most reasonable measures – yet you would lose. Plurality voting in fact appears to promote the emergence of two-party systems. Political scientists call this Duverger’s Law.
When there are two major candidates and some much weaker third-party candidates, plurality voting leads to “spoiler” problems. The weak candidates can change the outcome, sometimes in ways that their supporters find highly undesirable. For instance, the presence of Green Party candidate Ralph Nader on the presidential ballot in Florida in 2000 may very well have caused Al Gore to lose Florida, and thereby the presidency, even though it’s likely that a large majority of Nader voters preferred Gore to George Bush.
Attempts to improve plurality voting have a long history, with primaries in the U.S. as well as runoff rounds in presidential elections in France, Brazil and other countries.
Instant runoff and its problems
With instant runoff, every voter ranks the candidates. The candidate who is ranked first by the fewest voters is then removed from the ballots, and candidates who were ranked underneath the removed candidate move up by one notch. Then the process is repeated until only one candidate remains. That candidate wins.
In practice, one would want to allow voters to rank only some, not all, of the candidates, and one would want to allow ties. These are complications that are important, but also easy to deal with. For simplicity, we’ll assume here that all voters rank all candidates, with no ties.
When there are two strong candidates and some much weaker third-party candidates, instant runoff clearly does away with the spoiler problem. Weak candidates are eliminated early on.
For example, if instant runoff had been used in the 2000 presidential election in Florida, Gore would likely have been president. Nader would have been eliminated early on in the process, and those among his 97,421 voters who preferred Gore over Bush would have been counted as Gore voters. Considering that the final official margin by which Bush won Florida was 537, it seems likely that this would have changed the outcome.
Unfortunately, instant runoff – just like plurality voting – also immediately eliminates the candidate who is everyone’s second choice but nobody’s first.
And, just like plurality voting, instant runoff does not work well when there are more than two strong candidates. It can then produce quite arbitrary outcomes. If there are five strong candidates, should you really be eliminated just because 18 percent of voters put you first, while the other four candidates were placed first by 19 to 22 percent of voters? Shouldn’t we look at how many voters put you second, for instance, before ruling you out as the winner?
Condorcet and Borda
Two French noblemen of the 1700s thought about how to organize multi-candidate elections: the Marqis de Condorcet and Jean-Charles de Borda. (Condorcet was friends with Thomas Jefferson, who appears to have paid little attention to Condorcet’s writings about voting.)
Condorcet suggested that, if an absolute majority – more than half the voters – prefers Candidate X to Candidate Y, then Candidate Y should not be the winner. That seems very reasonable. Why not make the majority happier by making X the winner?
Unfortunately, when there are more than two candidates, this principle can easily rule out everyone. There can be a situation where, say, 55 percent of voters prefer Candidate A to Candidate B, 60 percent prefer B to C and 65 percent prefer C to A.
Condorcet didn’t say what should happen in such a case. His proposal refers only to situations in which there is a single candidate, the “Condorcet candidate,” who would beat every other candidate in head-to-head contest. He suggested that a Condorcet candidate, if there is one, should win.
As sensible as this sounds, both plurality voting and instant runoff violate it. Take my earlier example of an election with five candidates. If you are ranked second by every single voter, you might well win head-to-head contests against each of your four competitors. But, under plurality voting or instant runoff, you will lose.
Borda proposed his own election method that allots each candidate points based on their ranking. For instance, if there are five candidates, then Borda proposes to give a candidate five points for first place on a voter’s ballot, four points for second place, and so on.
Unfortunately, Borda and Condorcet can clash in a rather dramatic way. Even if an absolute majority of voters place you first, Borda may have you lose if most of the other voters strongly dislike you.
Borda’s method tends to handicap polarizing candidates. This seems like a good thing. However, if an absolute majority of voters place me first, then I should win, according to Condorcet, and most people would probably agree. When Borda’s method makes me lose because I am strongly disliked by a substantial minority, one could – and Condorcet would – argue that this goes a bit too far.
Merging Condorcet’s and Borda’s ideas
Merging Condorcet’s and Borda’s ideas creates an election method which, in my view, is much better than instant runoff, and just as simple. (I discuss this method at greater length in my textbook on this subject.)
In the system I propose, voters rank candidates, as in instant runoff and many other election methods. The outcome is then evaluated in two stages: a “Condorcet stage” where we pick out the strongest candidates, followed by a “Borda stage” where we identify the winner.
In the Condorcet stage, we determine the “strong” candidates. We define the “strong” candidates to be the smallest group of candidates with the property that everybody inside the group would beat everybody outside the group in two-person races. (This is also often called the Smith set, after the mathematician John H. Smith.) For instance, if there is a Condorcet candidate X, then X is the only strong candidate.
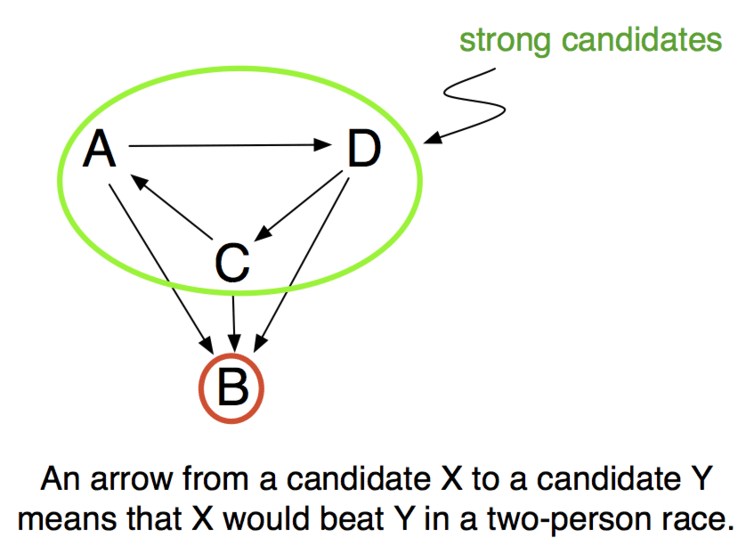
We then remove all candidates who are not strong from the ballots, and move on to the Borda stage. The winner is computed with the reduced ballots based on Borda’s method.
In a presidential election, voters would all rank all the candidates: Republicans, Democrats and others. A computer would then determine the strong candidates. (No cause for alarm: Anybody who knows the election results could quite easily verify the computer’s work by hand.) Borda’s method would then decide from among this group.
I believe that many of the people who now support instant runoff should, and would, like this scheme even more. It eliminates weak candidates right away, removing the possibility of spoiler effects. It allows two candidates from the same party to run without interfering with each other so much that neither can win. It allows more than two strong candidates to emerge. When there are several strong candidates, the results are intuitively sensible. The method retains one of the advantages of Borda’s method – namely that polarizing candidates often lose – but, unlike Borda’s method, it does not allow a Condorcet candidate to lose. Equally importantly, the method is simple and transparent, and therefore might be politically viable.
![]() There is no doubt that the issue is important: We cannot value democracy, yet refuse to think about the question how to conduct elections in a fair way.
There is no doubt that the issue is important: We cannot value democracy, yet refuse to think about the question how to conduct elections in a fair way.
This article was originally published on The Conversation. Read the original article.



Rate and Review
Rate this article
Review this article
Log into OpenLearn to leave reviews and join in the conversation.
Article reviews