4.2 Subdivisions

In this subsection we formalise the idea of a net by introducing a useful concept called a subdivision of a surface. This is a standard kind of net drawn on a surface, and is defined in terms of vertices, edges and faces. It leads to the idea of the Euler characteristic of the surface.

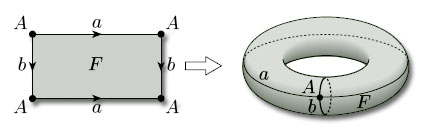
All surfaces obtained from polygons by identifying edges arise from a net (of sorts) consisting of a single polygonal face, together with the edges and vertices that remain after the identifications have been carried out. For example, a torus is obtained from a rectangle by identifying edges: the top and bottom edges become the same, the left and right edges become the same, the four vertices of the rectangle become the same, and there is just one face, as shown in Figure 78. This ‘net’ therefore has one vertex (A), two edges (a and b) and one face (F): the face F is what is left after all the vertices and edges have been removed.

Figure 78

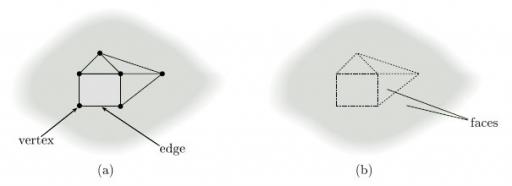
We now try to formalise the idea of a net of polygons on a surface so as to include both this case and the nets described in the previous subsection: the result is called a subdivision of the surface. We start with the surface and mark a set of vertices (points) on it, joining them by edges (non-crossing curves) to produce a connected graph, as shown in Figure 79(a). If we now remove the vertices and edges of this graph from the surface, as shown in Figure 79(b), then their complement splits into a finite number of pieces. If these pieces are all homeomorphic to open discs, then the vertices and edges define a subdivision of the surface, and the disc-like regions are the faces of the subdivision.

Maximise

Figure 79

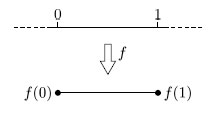
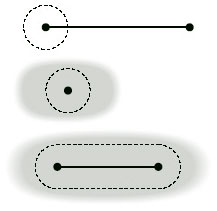
Before we can write down a formal definition of a subdivision of a surface, we must formalise the idea of an edge: an edge of a subdivision is the image of the open interval (0, 1) under a one-one continuous map f of the closed interval [0, 1], as Figure 80 illustrates. The points f(0) and f(1) are the endpoints of the edge. (The endpoints are not part of the edge and may coincide.)

Figure 80

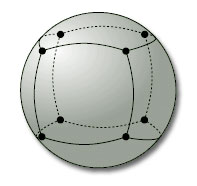
An example of a subdivision is the ‘cube subdivision’ of a sphere, shown in Figure 81, which has 8 vertices, 12 edges and 6 faces.

Figure 81

It is natural to say that two adjacent faces ‘meet along their common edge’, and that edges ‘meet at a vertex’, but strictly speaking this is incorrect since the vertices, edges and faces of a subdivision are disjoint.

To allow us to use such natural phrases, we shall say that:

• a vertex belongs to an edge if every open set containing the vertex contains points of the edge, so the vertex is in the closure of the edge;

• a vertex belongs to a face if every open set containing the vertex contains points of the face, thus the vertex is in the closure of the face;

• an edge belongs to a face if every open set containing the edge contains points of the face, thus the edge is in the closure of the face.

These relationships are illustrated in Figure 82. They allow us to say that two edges or faces meet at a vertex if there is a vertex that belongs to both of them, and that two faces meet at an edge if there is an edge that belongs to both of them. They also allow us to say that a face has a number of edges and vertices, namely those edges and vertices that belong to it. We shall also say that the edges that meet at a vertex are the incident edges of that vertex.

Figure 82

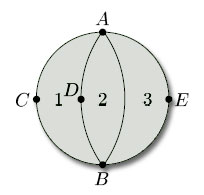
To illustrate this terminology, consider the subdivision of a closed disc shown in Figure 83, which has 5 vertices (A, B, C, D, E), 7 edges (AB, AC, AD, AE, BC, BD, BE) and 3 faces (1, 2, 3). Faces 1 and 2 meet at edges AD and BD and at vertices A, B and D; faces 2 and 3 meet at edge AB and at vertices A and B; faces 1 and 3 meet only at vertices A and B. Edges AC and BC meet at vertex C; edges AC and AD meet at vertex A; edges AD and BC do not meet; and so on. Face 1 has 4 edges (AC, AD, BC, BD) and 4 vertices (A, B, C, D); face 2 has 3 edges (AB, AD, BD) and 3 vertices (A, B, D); face 3 has 3 edges (AB, AE, BE) and 3 vertices (A, B, E).

Figure 83

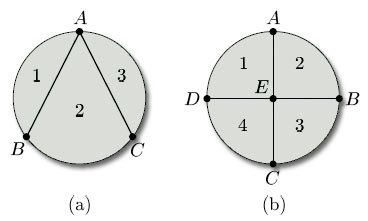
Problem 18

List the vertices, edges and faces of each of the subdivisions of a closed disc in Figure 84. Describe where face 1 meets the other faces in each case. How many edges and vertices does face 3 have in each case?

Figure 84

Answer

(a) vertices {A, B, C},

edges {AB (twice), AC (twice), BC};

faces {1, 2 ,3}.

Faces 1 and 2 meet at the inner edge AB and at vertices A and B. Faces 1 and 3 meet at vertex A only. Face 3 has 2 edges (both from A to C) and 2 vertices (A and C).

(b) vertices {A, B, C, D, E},

edges {AB, BC, CD, DA, AE, BE, CE, DE},

faces {1, 2, 3, 4}.

Faces 1 and 2 meet at the edge AE and at vertices A and E. Faces 1 and 3 meet at vertex E only. Faces 1 and 4 meet at edge DE and at vertices D and E. Face 3 has 3 edges (BC, BE, CE) and 3 vertices (B, C and E).

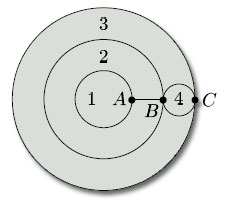
We noted earlier that the endpoints of an edge may coincide. This means that an edge can meet itself, as is illustrated by the circular edges in the subdivision of a closed disc shown in Figure 85. This figure also shows that a face may meet itself along an edge – face 2 meets itself along the edge AB (and of course at the vertices A and B) – and also a face may meet itself at a vertex or vertices but not along an edge – face 3 meets itself at vertices B and C only.

Figure 85

From the definition of a subdivision and the examples we have given, we may deduce the following properties of subdivisions of surfaces:

• each point of the surface must be a vertex, or lie on an edge, or lie in a face;

• faces meet only at vertices and edges;

• two faces may meet at one or more vertices;

• two faces may meet at one or more edges;

• edges meet only at vertices;

• an edge may belong to one or two faces;

• an edge may have one or two vertices;

• a vertex may belong to one or more faces;

• a vertex may belong to one or more edges.