5.2.1 Proof
We check that Tf satisfies conditions (T1)–(T3) for a topology.
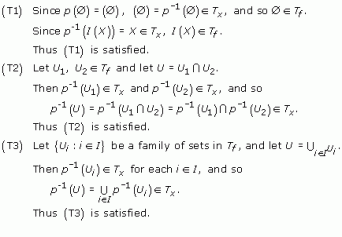
Since (T1)–(T3) are satisfied, Tf is a topology on I(X).
Thus (I(X),Tf) is a topological space. We give the topology Tf a special name.
Definition
The topology Tf defined in Theorem 15 is the identification topology for X under f.
We now use F to create a topology on Y = f(X). We define a subset U of Y to be open if F−1(U) is an open subset of X.
Recall that F([x]) = f(x).
Problem 29
Show that the family TY of open sets defined in this way comprises a topology on Y.
Answer
We check (T1)–(T3).
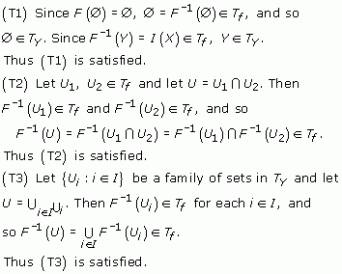
Since (T1)–(T3) are satisfied, TY is a topology on Y.
So we have a bijection F:I(X) → Y between the topological spaces (I(X),Tf) and (Y,TY). Furthermore, from the definitions of open sets in Tf and TY, we can deduce immediately that for each U ![]() TY, F−1(U)
TY, F−1(U) ![]() Tf and for each V
Tf and for each V ![]() Tf, F(V)
Tf, F(V) ![]() TY. Hence F is a homeomorphism between (I(X),Tf) and (Y,TY).
TY. Hence F is a homeomorphism between (I(X),Tf) and (Y,TY).
We have thus shown that the object created by identifying some or all of the edges of a polygon is a topological space homeomorphic to the identification space of the polygon. We now need to show that this topological space is Hausdorff and that every point has a disc-like or half-disc-like neighbourhood, to demonstrate that the space is indeed a surface.
