1.2 Exploring the magnitude scale
To explore the magnitude scale in more detail, let’s take a look at where some familiar objects appear on the scale.
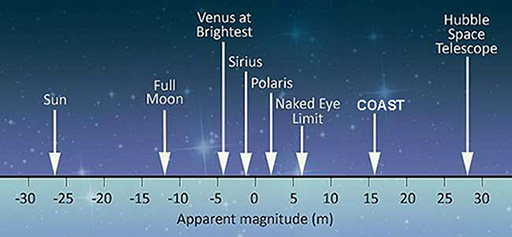
In Figure 2, the magnitude scale has been extended to include objects far brighter than the stars – including Venus, the Moon and the Sun. Being extremely bright, these have very large negative magnitude numbers.
In order to cover such a wide range of brightness, the magnitude scale works on a logarithmic principle. This is a mathematical term meaning that each step along the scale multiplies the brightness by a certain amount, rather than simply adding a fixed amount. Specifically, a change of five magnitudes represents an increase or decrease of 100 times in the brightness – so that for example, a magnitude +1 star is one hundred times brighter than a magnitude +6 star.
Breaking this down into individual steps along the scale a change of one magnitude is equal to an increase or decrease of approximately 2.5 times in brightness.
[Many other scales work on this logarithmic principle in order to cover a wide range – the Richter scale for earthquakes and the decibel scale for intensity of sound are two other examples of logarithmic scales. In both cases, each step along the scale represents a multiplication in the value being measured.]
Activity 2 Caculating the difference in brightness of stars
Two stars have magnitudes of +2.0 and +4.5 – a difference of 2.5 magnitudes.
How many times brighter is the magnitude +2.0 star than the magnitude +4.5 star ?
Answer
The stars differ in brightness by a factor of 10. To work this out, remember that a difference of 5 magnitudes multiplies the brightness by a factor of 100. Two steps of 2.5 makes a total change of 5 magnitudes, so each step of 2.5 magnitudes must multiply the brightness by 10. In this way, two steps of 2.5 gives a change of 10 × 10, which is 100.