1.3 Problem of points
You are now going to look at the ‘problem of points’, which was mentioned earlier. Specifically, the problem involves a game of chance with two players. Both players, each of whom have an equal chance of winning, have put up the same stake, and the first player who collects a certain number of points wins the game and collects the entire stake. Suppose, however, that the game is interrupted and cannot continue before either player has won. How then should the winnings be divided? Clearly the player who has already accumulated the greater number of points should receive a greater share of the winnings, but it is not so clear what that share should be. How can this be resolved?
Let’s look at a specific example. Suppose that the two players, Alex and Bill, are rolling a single die. Alex scores a point if the die shows a 4, 5 or 6, and Bill scores a point otherwise. In other words, on each roll of the die they each have an equal chance of scoring a point. The total stakes are £60, which will go to the person who first scores a total of 3 points. If the game is interrupted when Alex has scored 2 points and Bill 1 point, how should they divide the £60?
There are two ways of looking at this. Either you can focus on what has happened in the past or you can focus on what may happen in the future. Taking the first approach here, Alex would walk away with all the winnings and Bill would get nothing, because the only knowledge you have is that Alex is closer to a winning score of 3 points than Bill is.
Question 1
There is a problem with this solution. Can you see what it is?
Answer
No value has been attached to the fact that Bill was still in the game when it was interrupted. He still had a chance of scoring 3 points before Alex, and this chance is certainly worth something.
What happens if you focus on the future instead? What possible outcomes can there be? Either Alex wins the next round and wins the game, or Bill wins the next round, and they go to a final round which either one of them can win. There are therefore three possible outcomes, two of which end with Alex as the winner. You might think that this approach means that Alex should get 2/3 of the stake (£40) but it turns out that this too is wrong!
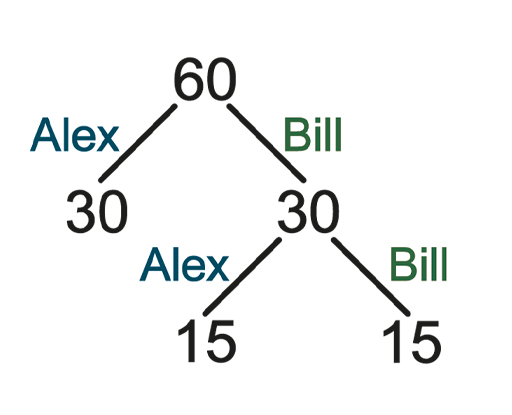
It was Blaise Pascal who worked out the correct solution, which goes as follows. Alex has a 50% chance of winning in one further round, in which case she would get the entire stake of £60. But if Bill wins that round, then, since they are each equally likely to win the final round, they could at this stage (before they play the final round) divide the stake equally between them so that they would get £30 each. In either case, Alex is guaranteed £30. So, the other £30 should be split equally between them, giving Alex a total of £45 and Bill a total of £15. This can be pictured in the following way.