Language, notation and formulas
Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Friday, 26 April 2024, 9:14 AM
Language, notation and formulas
Introduction
An integral part of learning mathematics involves communication.
Writing mathematics is a specific skill which needs to be developed and practised: there is a lot of difference between putting down a few symbols for your own use and writing a mathematical solution intended for someone else to read. In attempting mathematical questions, you may previously have written down very little, just enough, perhaps, to convince yourself that you could answer the questions. This may suffice now, but you may want to use your notes and solutions for revision so you will want them to be self-contained, able to stand on their own and easy to read. This will also be the case if you are writing mathematics for somebody else to read.
This OpenLearn course provides a sample of level 1 study in Mathematics.
Learning outcomes
After studying this course, you should be able to:
lay out and, where appropriate, label simple mathematical arguments
understand the precise mathematical meaning of certain common English words
understand and use common mathematical symbols
write clear, unambiguous mathematical solutions using appropriate notation
identify and modify some sources of ambiguity or inappropriate use of notation in a mathematical solution.
1 Communicating mathematics
1.1 Writing mathematics
How do you write mathematics that can be read and easily understood by anyone else, such as a tutor or another student?
It takes practice, but the following guidelines may be helpful.
Ensure that what you write consists of sentences. Too many people believe that mathematics is a language which is entirely made up of unfamiliar symbols. It is not. Many symbols act in part merely as abbreviations which, when read, can be translated back into spoken words.
Ensure that there are sufficient words of explanation so that the reader is led, line by line, through your proposed solution or argument.

1.2 Talking and writing mathematics
One way of testing whether or not you are conforming to the first guideline, is to read your solutions through aloud. Speaking aloud involves you in translating every symbol on the page into its verbal equivalent. If you find yourself needing to say more than is written on the page, you may need to expand your written account. To give you practice at this and at assessing the quality of some written mathematics, work through the animation below. The actual mathematics used is not important; just concentrate on the style of its presentation.
Working through the following animation should take you about forty minutes. The relevant frames are shown with the appropriate extract and you will need to answer using pen and paper. After each extract you will need to click on the play button to hear the next audio.
2 Reading mathematics
2.1 Layout
As mentioned in the animation in Section 1.2 writing mathematics has a lot in common with writing English. When you write mathematics, you should write in the equivalent of sentences, with full stops at the end. As in English, each new statement should follow on logically from the previous one or it should contain an indication that a new idea is being introduced. However, laying out mathematics differs from laying out English: because mathematics is more condensed than written English, it is often best to start each statement on a new line so that the various steps involved are readily apparent.
In writing mathematics you can use a mixture of words and symbols – symbols in mathematics are just shorthand for words. If you do not know the correct symbol, use the word itself.
Above all, make sure that you write so that somebody else can understand – that somebody might be yourself at a later date! It often helps to read aloud the mathematics that you have written to see if it makes sense.
Example 1
Read the following mathematics aloud:
(a) 24.67 − 12.45 = 12.22
(b) 3 × 4 = 4× 3 = 12.
Answer
(a) Twenty-four point six seven minus twelve point four five equals twelve point two two.
(b) Three times four equals four times three which is equal to twelve.
2.1.1 Try some yourself
Activity 1
Read the following expression out aloud or write it out in full in words:
(a) 21 + 34 = 55
Answer
(a) Twenty-one plus thirty-four equals fifty-five.
2.2 Using the equals sign
As mentioned previously, one of the most misused mathematical symbols is the equals sign, =. It stands for the verb ‘equals’ or the phrase ‘is equal to’ or ‘which equals’, and so it should only come between two things that are equal.
Example 2
Which of the equals signs should not be included in these calculations?
(a) 24.67 − 12.45 = 12.22
(b) 6.4 + 23.34 = 29.74
(c)
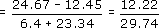
Answer
The equals signs in (a) and (b) are used correctly, but the first sign in (c) is not. This equals sign is not between two things that are equal, and consequently it should not be there. Also it is at the beginning of a sentence, and when you read it aloud it does not make sense. It would be better replaced by a word like ‘hence’ or ‘so’.
2.2.1 Try some yourself
Activity 2
Here is a poor example of mathematical writing, although the final answer is correct. Rewrite it, correcting the layout and the mathematical punctuation.
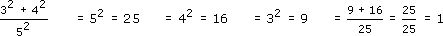
Answer
There are many possible alternatives – here is one of them.
Since 52 = 25, 42 = 16 and 32 = 9,
hence
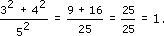
2.3 Link words
A lot of people use the equals sign wrongly in places where another word or phrase might actually make the meaning clearer. Sometimes a link word or phrase is useful at the beginning of a mathematical sentence: examples include ‘So’, ‘This implies’ or ‘It follows that’ or ‘Hence’.
Example 3
Add link words and punctuation to the calculation below to help somebody else to follow it.
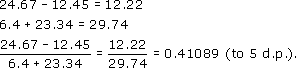
Answer
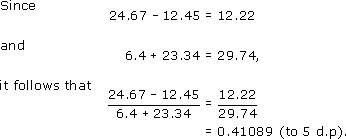
Notice that mathematical calculations are often easier to read if all the equals signs are aligned underneath one another.
2.3.1 Try some yourself
Activity 3
In the following two pieces of mathematical writing, remove or replace any inappropriate equals signs, and add link words and punctuation to help somebody else understand the mathematics.
(a)
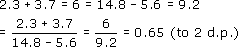
(b) (3.2)2 = 10.24 = (8.5)2 = 72.25 = 10.24 + 72.25 = 82.49
Answer
The versions given below are not the only possibilities. You may have used other words, but check that you have written in whole sentences with full stops at the end.
(a)
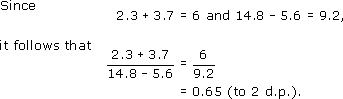
(b)
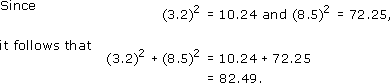
2.4 Labelling lines
Sometimes you may want to refer to mathematical sentences or phrases further up your work. You can label such sentences and then refer back by label. Thus, Example 3 could be laid out as follows.
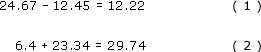
So, from (1) and (2),
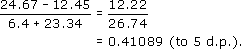
2.4.1 Try some yourself
Activity 4
Two labels have been omitted in the mathematics below. Where should they go to make sense of the argument?
Since
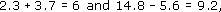
it follows that
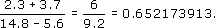
Now
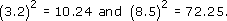
Hence
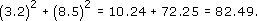
So, from (1) and (2),
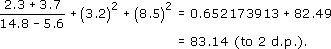
Answer
Since
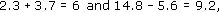
it follows that
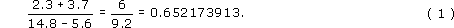
Now
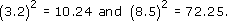
Hence
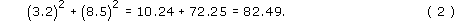
So, from (1) and (2),
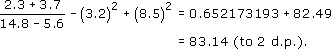
2.5 Vocabulary
In mathematics, some words are used in a more precise way than in English. It is important that a mathematical argument is unambiguous; therefore words that can be used in several contexts in English usually take only one meaning in mathematics. For instance, in English the word ‘sum’ might mean any calculation, but it has a precise mathematical meaning as exemplified by ‘The sum of 456 and 789 is 1245’. Similarly, in English the word ‘product’ can have a variety of meanings, but in mathematics the product of two numbers is the result obtained by multiplying those numbers together.
Below is a list of mathematical words and phrases, together with their mathematical meanings and examples of their use. You will have come across some of them before. Read them carefully and try to see the connections with the meanings that the words have in everyday English. You may well wish to copy the table into your notes and add to it in your future studies.
| Word/phrase | Mathematical meaning | Example of use |
|---|---|---|
| Even number | A whole number that is exactly divisible by two (that is, it results in a whole number when divided by two). | 432 is an even number. |
| Odd number | A whole number that is not exactly divisible by two. | 321 is an odd number. |
| Sum | The addition of numbers. | The sum of 123 and 456 is 579. |
| Difference | The numerical difference between two numbers, or the positive result of subtracting one number from the other. | The difference between 24 and 42 is 18. The difference between 5 and −2 is 7. |
| Product | The result of multiplying numbers together. | The product of 3, 4 and 5 is 60. |
| Quotient | One number divided by another. | The quotient 60 ÷ 12 is 5. |
| Exponent | The power to which a number is raised. | In the expression (2.6)4, 4 is the exponent. |
| Perimeter | The outer boundary of a geometric figure (also the length of that boundary). | The perimeter of the figure was drawn in red. |
| Circle | A geometric figure in which every point on its perimeter is the same distance (the radius) from its centre. | The circle has a radius of 4 cm. |
| Equation | One expression equaling another. | The equation 9 − 6 = 3. |
| Inequality | One expression being less than or greater than another. | 3 |
2.5.1 Try some yourself
Activity 5
How would you add the following words to the list:
decimal, fraction, positive, negative.
For each one, give the mathematical meaning and an example of its use.
Answer
There are many different correct answers to this question. However, make sure that the meanings you have given are equivalent to the ones below.
| Word | Mathematical meaning | Example of use |
|---|---|---|
| Decimal | A number expressed in terms of tenths, hundredths, etc. | A quarter expressed as a decimal is 0.25. |
| Fraction | One whole number over another. | 0.75 expressed as a fraction is |
| Positive | Greater than zero. | 2 is a positive number. |
| Negative | Less than zero. | −2 is a negative number. |
2.6 Making sense of symbols
Mathematical symbols are a shorthand way of writing words or phrases that crop up often in mathematical writing.
2.6.1 Arithmetical symbols
You will have already met the symbols for the basic arithmetical operations, which are +, −, × and ÷, but you may not have met some of the alternative ways of writing × and ÷.
To recap, the main symbols for arithmetical operations are:

There are other alternatives to × and * for multiplication. Sometimes, provided there is no risk of ambiguity, no symbol is used, just as sometimes the words ‘multiplied by’ or ‘times’ can be omitted in speech: for example, two fours or five fives means two times four or five times five, respectively. So, instead of writing 3 × (4 + 5), you can just write 3(4 + 5) and save one symbol. Mathematicians like to be as concise as possible! Brackets avoid ambiguity in mathematical expressions.
An alternative to ÷ and / for division is a fractional notation: for example, ![]() means ‘add three and six, and then divide by four’. The slash symbol / is sometimes used for fractions: thus, three-quarters may be written as 3/4. Many calculators use this notation to display fractions.
means ‘add three and six, and then divide by four’. The slash symbol / is sometimes used for fractions: thus, three-quarters may be written as 3/4. Many calculators use this notation to display fractions.
Example 4
What do the following expressions mean?
(a) 5/(3 + 2)
(b) 5/3 + 2
(c) 4(8 − 5)
Answer
(a) Divide 5 by the sum of 3 and 2. (This gives 1.)
(b) Divide 5 by 3 and then add to 2, or
 added to 2. (This gives
added to 2. (This gives 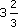 .)
.)(c) Multiply 4 by the difference between 8 and 5. (This gives 12.)
2.6.2 Try some yourself
Activity 6
Read the following expression out aloud or write it out in full in words:
(a) 3 × 4 + 3 × 5 = 3 (4 + 5).
Answer
(a) Three times four, plus three times five equals three times the sum of four and five.
Activity 7
Which mathematical operations are implied by these words when used in a mathematical sense?
(a) Sum
(b) Difference
(c) Product
(d) Quotient
State the operations in both words and symbols.
Answer
(a) Sum implies addition or +.
(b) Difference implies subtraction or −.
(c) Product implies multiplication or ×.
(d) Quotient implies division or ÷.
2.7 Powers and roots
There are several symbols for powers and roots: for instance, 24 means ‘2 to the power 4’. An alternative to 24 is 2![]() 4, where the symbol
4, where the symbol ![]() means ‘to the power’. This symbol is often used by computers and calculators.
means ‘to the power’. This symbol is often used by computers and calculators.
A related symbol is the square root symbol, as in ![]() meaning the positive square root of 25 (that is, 5). Symbols for other roots, are exemplified by
meaning the positive square root of 25 (that is, 5). Symbols for other roots, are exemplified by ![]() meaning the cube root of 8 (that is, 2).
meaning the cube root of 8 (that is, 2).
Raising to the power −1 gives the symbol for a reciprocal: thus, 6−1 means the reciprocal of 6, or ![]() . The symbols used by calculators for scientific notation often involve the letter E: for example, 3.1E2 means 3.1 × 102, or 310.
. The symbols used by calculators for scientific notation often involve the letter E: for example, 3.1E2 means 3.1 × 102, or 310.
Example 5
What do the following expressions mean?
(a) 52
(b)
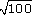
(c) (5 + 8)2
(d) 2−1
(e)
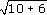
Answer
(a) Square 5. (This gives 25.)
(b) Positive square root of 100 (This gives 10.)
(c) Add 5 and 8, and then square the result. (This gives 169.)
(d) The reciprocal of 2. (This gives
 or 0.5.)
or 0.5.)(e) The square root of the sum of 10 and 6. (That is, 4.)
2.7.1 Try some yourself
Activity 8
Evaluate the following:
(a) 34
(b) 3

(c) 5−1
(d)
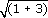
(e) (6 − 2)3
Answer
(a) 34 = 3 × 3 × 3 × 3 = 81.
(b) 3
 = 3 (since 3 × 3 × 3 = 27).
= 3 (since 3 × 3 × 3 = 27).(c) 5−1 =
 or 0.2.
or 0.2.(d)
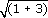 =
= 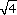 = 2.
= 2.(e) (6 − 2)3 = 43 = 4 × 4 × 4 = 64.
2.8 Relationship symbols
There are also symbols that show the relationship between numbers or quantities. Two common ones are = and ![]() , but there are several other symbols of this type.
, but there are several other symbols of this type.
Symbols indicating relationships include:
= means ‘equals’;
≠ means ‘does not equal’;
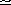 means ‘is approximately equal to’;
means ‘is approximately equal to’;> means ‘is greater than’;
≤ means ‘is less than or equal to’;
≥ means ‘is greater than or equal to’.
Other symbols that are sometimes used include:
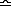 means ‘is approximately equal to’ (an older version);
means ‘is approximately equal to’ (an older version);≡ means ‘is exactly equivalent to’;
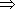 means ‘implies’;
means ‘implies’;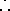 means ‘therefore’;
means ‘therefore’; means ‘because’.
means ‘because’.
Another type of symbol that you come across are abbreviations for units of measurement: for example, m for metres, kg for kilograms, and h for hours, and in imperial units ft for feet
Example 6
What do the following mean?
(a) time > 2s
(b) height ≤ 100 m
(c)
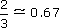
Answer
(a) The time is greater than 2 seconds.
(b) The height is less than or equal to 100 metres.
(c) Two-thirds is approximately equal to 0.67.
You will meet many symbols in your mathematical studies. It is important that you are sure what each one means in any given context, so that you can read it and use it appropriately.
2.8.1 Try some yourself
Activity 9
What do the following mean?
(a) (5 + 8)/(4 − 2)
(b) 5 + 8/4 − 2
(c) (4 + 5)(5 − 2)
(d)
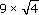
(e)
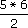
(f)
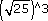
(g) (12 − 9)−1
Answer
(a) Add 5 and 8, and then divide the result by the difference between 4 and 2. (This gives
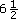 .)
.)(b) Add 5 to the division 8/4, and then subtract 2. (This gives 5.)
(c) Multiply the sum of 4 and 5 by the difference between 5 and 2. (This gives 27.)
(d) Multiply 9 by the square root of 4. (This gives 18.)
(e) Multiply 5 by 6, and then divide by 2. (This gives 15.)
(f) The cube of the square root of 25. (That is, 125.)
(g) The reciprocal of 12 minus 9. (That is,
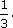 )
)
Activity 10
What do these symbols mean?
(a) =
(b)
(c) >
(d)
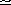
Answer
(a) = means ‘equals’ or ‘equal to’ or ‘which equals’.
(b) or ‘which is less than’.
(c) > means ‘greater than’ or ‘which is greater than’.
(d)
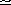 means ‘is approximately equal to’.
means ‘is approximately equal to’.
Activity 11
What do the following mean?
(a) mass ≥ 10 kg
(b) time 6 h
(c) 2/3 ≠ 0.67
Answer
(a) The mass is greater than or equal to 10 kg.
(b) The time is less than 2.4 million hours.
(c) Two-thirds (or 2 divided by 3) is not equal to 0.67.
3 Formulas
3.1 Word formulas
A formula is a rule or a generalisation. Word formulas – formulas that use English words rather than mathematical symbols – are so much a part of life that people often use them without realising that they are doing so. Here are some examples.
The cost of a purchase of oranges is the price per orange times the number of oranges.
The total cost of petrol is the price of petrol per litre times the number of litres.
The average speed is the distance travelled divided by the time taken.
The number of tins of paint needed to cover a wall is the area of the wall divided by the area covered by one tin of paint.
These word formulas can be written more clearly using mathematical symbols. Notice how brackets can be used for clarity.
Cost of oranges bought = (price per orange) × (number of oranges).
Cost of petrol = (price of petrol per litre) × (number of litres).
Average speed = (distance travelled)/(time taken).
Number of tins of paint needed = (area of wall)/(area covered by one tin).
Sometimes letters are used as shorthand in formulas.
Example 7
At constant speed, ‘distance is the product of speed and time’. Write this as a word formula and then shorten it by using symbols: d for distance, s for speed and t for time.
Answer
distance = (speed) × (time)
d = s × t or d = st
3.1.1 Try some yourself
Activity 12
Write the folowing as word formulas and then shorten them
(a) The area of a square is its length squared.
(b) The area of a rectangle is its length times its breadth.
(c) The area of a triangle is half its base times its height
Answer
(a) The area of a square = (length)2 = l2 where l stands for length.
(b) The area of a rectangle = (length) × (breadth) = l × b or lb where l stands for length and b for breadth.
(c) The area of a triangle is
 (base) × (height) =
(base) × (height) =  b × h or
b × h or  bh where b stands for base and h for height
bh where b stands for base and h for height
(Note it is important to be clear about what each letter represents).
3.2 Using formulas
Formulas are important because they describe general relationships, rather than specific numerical ones. For example, the tins of paint formula applies to every wall. To use such a formula you need to substitute specific values for the general terms, as the following examples show.
Example 8
If the price of petrol is 85 pence per litre and a driver buys 25.9 litres, what is the cost?
Answer
The formula is
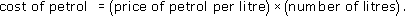
The price per litre is 85 pence and the number of litres is 25.9. So
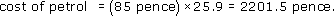
Rounded to the nearest penny, this is 2202 pence or £22.02.
Example 9
Suppose you are travelling on a UK motorway in a coach and you want to know how far the coach has travelled in the previous quarter of an hour. You glance over the shoulder of the driver and you see that the speed is a steady 70 miles per hour. Estimate how far you have travelled on the motorway in the last quarter of an hour, assuming a constant speed of 70 miles per hour.
Answer
The formula gives
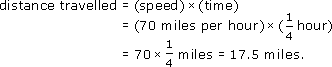
3.2.1 Try some yourself
Activity 13
You are planning to paint three rooms with total wall areas of 56, 38 and 40 square metres, using paint that comes in tins which claim to cover 15 square metres per tin. How many tins will you need for each room? And how many in total?
Answer
For the first room, with a wall area of 56 square metres,
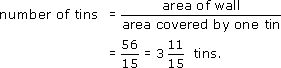
For the second room, with a wall area of 38 square metres,
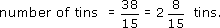
For the third room, with a wall area of 40 square metres,
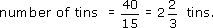
The total number of tins required will depend on whether you are planning to paint all the rooms in the same colour or not. If you are, the number of tins required will be
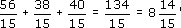
so you will need to buy 9 tins. If all the rooms are to be different colours, you will need to buy 4 tins for the first room, 3 for the second and 3 for the third – a total of 10 tins.
3.3 Units and formulas
As already noted, the units used in a formula must be consistent. For instance, in Example 9, the speed is in miles per hour, so the time travelled must be in hours and the distance travelled must be in miles. If one of the quantities is not in the correct units, then you need to change it before using the formula.
Example 10
Suppose you have been travelling in a car at a roughly constant speed of 50 miles per hour for 45 minutes. How far would you have travelled?
Answer
You need to change the time into hours in order for the units to be consistent. Thus, 45 minutes is ![]() hour. Then, from the formula,
hour. Then, from the formula,
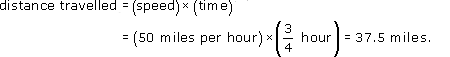
3.3.1 Try some yourself
Activity 14
If tomatoes cost 75 pence per kg, how much would 1.45 kg cost in pounds (£)?
Answer
The formula is
cost of tomatoes = (price per kilogram) × (number of kilograms).
The price per kilogram is 75 pence, and the number of kilograms is 1.45. So the formula gives
cost of tomatoes = (75 pence) × 1.45 = 108.75
Rounded to the nearest penny this is 109 pence, or £1.09.
Activity 15
If you travel in a car at a constant speed of 60 km per hour, how far would you have travelled after 1.5 hours, after 2 hours 40 minutes and after three and a half hours?
Answer
The formula is
distance travelled = (speed) × (time).
So, after 1.5 hours,
distance travelled = (60 km per hour) × (1.5 hours) = 90 km.
As 2 hours 40 minutes is ![]() hours, or
hours, or ![]() hours, the formula gives
hours, the formula gives
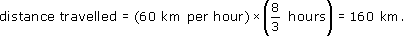
For three and a half hours (3.5 hours), the formula gives
distance travelled = (60 km per hour) × (3.5 hours) = 210 km.
Activity 16
3 Suppose you are selling a new lawn-edging strip and need to calculate the perimeters of lawns in order to quote prices to prospective customers.
The formula for the distance round the perimeter of a rectangular lawn is
perimeter = 2 × length + 2 × breadth.
Use this formula to find the perimeter of a lawn that is 10 m by 8 m.
Answer
The length of the lawn is 10 m and its breadth is 8 m. So, from the formula,
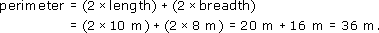
The perimeter of the lawn is 36 m.
Activity 17
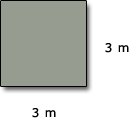
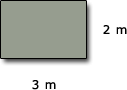
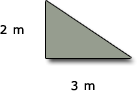
Use the formulas for areas given below to find the areas of the shapes in square metres (m2).
Area square = (length)2; Area rectangle = length × breadth; Area triangle = ![]() base × height
base × height
(a)
(b)
(c)
Answer
(a) Area square = (length)2 = (3 m)2 = 9 m2
(b) Area rectangle = length × breadth = 3 m × 2 m = 6 m2
(c) Area triangle =
 base × height =
base × height =  × 3 m × 2 m =
× 3 m × 2 m =  × 6 m2 = 3 m2
× 6 m2 = 3 m2
3.4 Converting units by using a formula
It is sometimes necessary to convert from one unit of measurement to another. You can use a formula in order to do this.
Example 11
Use the formula 1 pint = 0.5683 litres (to 4 s.f.) to calculate the number of litres in 8 pints (or 1 gallon). Give your answer to 3 significant figures.
Answer
As 1 pint is 0.5683 litre, it follows that 8 pints will be 8 times this:
8 pints = 8 × (0.5683 litre) = 4.55 litres (to 3 s.f.).
Sometimes the conversion formula that is given is in the opposite direction from the one you want. However, it is possible to turn such formulas round. For example, since 1 km = 1000 m, it follows that
![]()
Example 12
Turn the formula 1 mile = 1.609 km round to obtain 1 km in miles. Give your answer to 3 significant figures.
Answer
The formula can be written as
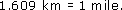
Dividing by 1.609 gives
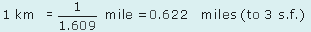
3.4.1 Try some yourself
Activity 18
1 Use the formula 1 mile = 1.609 km to find 12 miles in kilometres rounding your answer to 3 significant figures.
Answer
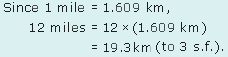
Activity 19
Turn the following formulas round to obtain centimetres in terms of inches, and grams in terms of pounds giving your answer to 4 decimal places:
1 inch = 2.54 cm;
1 Ib = 453.6 g (to 4 s.f.).
How many pounds are there in a kilogram?
Answer
From 2.54 cm = 1 inch, it follows that
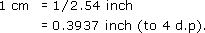
From 453.6 g = 1 lb, it follows that
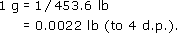
Since 1 kg is 1000 g,
Activity 20
You sell lawn-edging strip by the metre, but some customers have measured their lawns in feet so you have to convert their measurements into metres.
You know the perimeter of a rectangular lawn is:
perimeter = 2 × length + 2 × breadth.
Check whether it makes a difference if you convert to metres before or after you apply the formula.
(a) Use 1 ft = 0.3048 m to convert the measurements of a lawn that is 12.5 ft by 10 ft into metres. Then use the formula given above to find the perimeter of the lawn in metres.
(b) Use the formula given above to find the perimeter of the lawn in feet, and then convert this into metres.
Answer
(a) As 1 ft = 0.3048 m, it follows that
12.5 ft = 12.5 × 0.3048 m = 3.810 m
and
10 ft = 10 × 0.3048 m = 3.048 m.
Therefore the lawn is 3.810 m by 3.048 m.
From the formula for the perimeter,
perimeter = (2 × 3.810 m) + (2 × 3.048 m) = 13.716 m.
So the perimeter of the lawn in metres is 13.716 m.
(b) From the formula for the perimeter,
perimeter = (2 × 12.5 ft) + (2 × 10 ft) = 45 ft.
So the perimeter of the lawn in feet is 45 ft.
To convert this into metres, use 1 ft = 0.3048 m, then
45 ft = 45 × 0.3048 m = 13.716 m.
This is the same answer for the perimeter as in part (a). However, the method in part (b) is quicker and, as it involves fewer calculations, it affords less opportunity for making mistakes.
A further point to bear in mind is that the perimeter formula requires consistent units – you cannot, for instance, use length measured in feet and breadth measured in metres.
4 The format of questions
4.1 Understanding the question
Before you can attempt a question, you must read and understand it. This may sound obvious but you will need to know, before you start, what is expected by way of an answer. In particular, you will need to know the meaning of the instructions contained in the question. This section contains a discussion of the precise meanings attached to words like ‘find’, ‘show’, ‘write down’ and ‘determine’ in mathematics questions. The different types of instruction are illustrated by posing several questions all based on the same initial problem.
4.1.1 ‘Write down’ question
Example 13
Suppose you plan to redecorate your bathroom. The end wall has the following shape, with dimensions as shown on the diagram. The quality of the plasterwork is not good and you are considering tiling the wall.
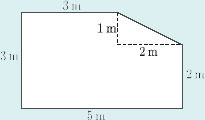
Write down the area of this wall. [4]
The number [4] at the right-hand side means there are four marks awarded for a correct solution. The marks give an indication of the length of answer expected. For example, if a question is in two parts, the first of which is allocated two marks and the second eight marks, then you would expect the first part to have a shorter and more straightforward solution than the second. Here, four marks would be awarded for stating the answer correctly, as in the solution below, because all you were asked to do was to ‘write down’ the area.
Solution A to Example 13
![]()
Comment
This solution does get full marks, but if 14 had been the wrong value the mark would have been zero. It is therefore a good idea to show working even when it is not required; some marks can be awarded for a wrong answer if there is an indication of a correct method being used.
4.2 A better solution
Here is an improved solution which shows working.
Example 13
Suppose you plan to redecorate your bathroom. The end wall has the following shape, with dimensions as shown on the diagram. The quality of the plasterwork is not good and you are considering tiling the wall.

Write down the area of this wall. [4]
Solution B to Example 13

Here the area is broken down into manageable parts and each area is found before the total area is stated. Had one of the areas been wrongly calculated, only one mark would have been deducted and the remainder would have been marked on a ‘follow through’ basis, giving almost full marks when a small error has been made. ‘Follow through’ means that credit is given for the method, even though the wrong value has been used.
When asked to ‘write down’ a solution, try to judge how much working to give by looking at the number of marks available for a correct solution.
4.3 ‘Find’ questions
Example 14
Suppose you have decided to tile the wall using square tiles of side 10 cm. You are proposing to use the tiles across the full 5 metre width of the wall up to a height of 1.8 m.
Find the number of boxes of tiles that you will require to cover the wall if the tiles are sold in boxes of twenty-five. [4]
The word ‘find’ implies some reasoning is required. Although the following solution contains an error (so it does not get full marks), it is nevertheless worthy of credit. Note how marks are awarded for correct reasoning and justification.
Solution A to Example 14
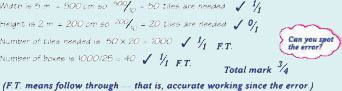
The error occurs in line 2 where the height of the tiles has been taken as 2 m not 1.8 m. However, credit is gained for those parts that are correct, including correct work following the error.
Solution B to Example 14
![]()
Comment
By contrast, this correct answer gets only the single final mark – the reasoning and justification marks are forfeited.
4.4 ‘Show that ’ questions
In this type of question you are given the answer! All the marks are allocated for correct reasoning and justification.
Example 15
Suppose you now decide to place your new bath (length 1.7 m, height 0.8 m) against this wall as shown in the diagram below.
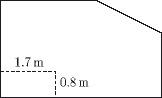
Given that you still intend to have the tiles to a height of 1.8 m, this means that you will not need so many tiles now. If a box of twenty-five tiles costs £14.75, show that the cost of tiling this wall will be £457.25. [7]
Note that the question says ‘show that’. So no marks are allocated for the final cost. This is reflected in the way the marks have been awarded in the following solution to Example 15
Solution to Example 15

Comment
This is one of several correct methods of showing that the cost will be £457.25. Any other correct method will also gain full marks.
4.5 Questions and answers
The following table summarises some of the types of instructions you will encounter.
| Write down … | Determine … | Show … |
| What is… | Find … | Prove … |
| Calculate … | ||
| A simple answer will do but generally give some working. | Justification for your answer is required. This will be reflected in the marks. | The answer is given to you. All marks awarded for a convincing argument. |
You may like to copy this table into your own notes and add to it if you encounter other question wording in the future.
5 Approaches to problem solving
You should not expect always to be able to read a problem and then just write down the answer. When you are faced with a written mathematical question or problem to solve, read it carefully. It is important that you get to grips with the question in two ways: first, that you absorb the information given; and second, that you find out what the question is really asking. Your solution will link the two. This method can be summarised by the following questions.
What do I know?
What do I want?
Try to decide not only what you know from the question itself, but also what you know from past experience which is at all relevant to the problem.
When you consider what you want, first decide whether you have to (a) find an answer or (b) show that something is true.
In order to get to grips with what a question is really about, it can often be helpful to begin by drawing a diagram.
If you are stuck, it may help to review your work. Try to write out your thoughts as clearly as possible so that you can easily see each step and the ideas they are based on.
You may need to leave the problem for a while and then come back to it, in order to see it more clearly. In this case, it is vital that you have written down what you have done so far. It may also be a good idea to talk to someone about it. The act of describing a problem to someone can often be enough to help you see what you should do to arrive at a solution. If there is nobody to talk to, try ‘talking to yourself’.
Always consider whether the answer you have come up with ‘makes sense’; that is, step back a bit and see whether it fits in with the other information that you have.
6 Writing out solutions
6.1 How a question is marked
When you tackle a mathematical question, it is often helpful to think about how it would be marked.
To give yourself some practice at this, in this section you will:
read and criticise sample solutions;
then read what the tutor wrote about them; and
see if any of the tutor's comments are applicable to your own solutions.
A billions problem
First write out a full solution to the following problem.
Example 16: Billions
You may think that you know what the word billion means but do you really have a feel for its size?
| (a) Write down one billion as a power of 10. | [3] |
| (b) Consider how far a billion centimetres (cm) is. Determine what one billion cm is in kilometres (km). How does it compare with the distance between Saturn and the Sun, which is 1427000 000 km? | [5] |
| (c) Now consider one billion seconds. Determine how long this is in years (round your answer to the nearest whole number). | [7] |
| (d) Finally, if there are 4 980 000 grains in 1 kilogram (kg) of sugar, show that one billion grains of sugar are approximately equivalent to 2 × 102 kg of sugar. | [5] |
6.1.2 Look at another solution
Now look at the sample solution below: consider both mathematical accuracy and style.
6.2 Another ‘billions’ solution
Pretend that you are the marker of another solution to the same problem. How would you mark Solution B?
Example 16 Billions
You may think that you know what the word billion means but do you really have a feel for its size?
| (a) Write down one billion as a power of 10. | [3] |
| (b) Consider how far a billion centimetres (cm) is. Determine what one billion cm is in kilometres (km). How does it compare with the distance between Saturn and the Sun, which is 1427000 000 km? | [5] |
| (c) Now consider one billion seconds. Determine how long this is in years (round your answer to the nearest whole number). | [7] |
| (d) Finally, if there are 4 980 000 grains in 1 kilogram (kg) of sugar, show that one billion grains of sugar are approximately equivalent to 2 × 102 kg of sugar. | [5] |
Sample Solution B to Example 16
(a) 109
(b) 109 ÷ 102 ÷ 103 = 104
(c) 109 ÷ 60 ÷ 60 ÷ 365 = 761
(d)
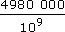 = 4.980 × 106 ÷ 109 = 4.980 × 10−3
= 4.980 × 106 ÷ 109 = 4.980 × 10−3
Click on ‘Reveal answer’ to see the tutor's marking.
6.3 Solving the riddle of St Ives
Write out your own solution to the following problem.
Example 17: St Ives
As I was going to St Ives
I met a man with seven wives.
Each wife had seven sacks.
Each sack had seven cats.
Each cat had seven kits.
Kits, cats, sacks and wives
How many were going to St Ives?
| (a) Write down the people I met. | [2] |
| (b) Find the number of wives, sacks, cats and kits. | [4] |
| (c) Show that the number of kits is 74. | [4] |
| (d) What is the answer to the riddle? | [2] |
Now comment on the sample solution which follow as if you were the tutor. Finally, use the tutor's comments to assess your own solution and comments.
Sample Solution A to Example 17

Click on ‘Reveal answer’ to see the tutor's marking.
6.4 Mark another St Ives' question
Now pretend your are the tutor marking a rather briefer response to the St Ives' riddle.
Example 17: St Ives
As I was going to St Ives
I met a man with seven wives.
Each wife had seven sacks.
Each sack had seven cats.
Each cat had seven kits.
Kits, cats, sacks and wives
How many were going to St Ives?
| (a) Write down the people I met. | [2] |
| (b) Find the number of wives, sacks, cats and kits. | [4] |
| (c) Show that the number of kits is 74. | [4] |
| (d) What is the answer to the riddle? | [2] |
Notice that the tutor suggests a clearer way of displaying the results. Solution A's method is also clearer. You will notice that the student lost marks for not really ‘showing’ that there were 74 kits, even though he or she probably understood this; the marks are for giving good, convincing reasoning.
6.5 Solutions to ‘making a lawn’
Learning from the marking of the previous questions, write out a good solution to the following problem.
Example 18: Making a lawn
Suppose you have some friends who are planning to put a new lawn in their garden. The lawn is to be 12 m by 14 m and they have a choice of either laying turf or sowing grass seed. You have been asked to help them decide between the two.
| (a) Write down the area of the lawn. | [3] |
| (b) The turf they can lay is sold in pieces, each of which is a square of grass measuring ½ m by ½ m. How many pieces of turf are needed to cover the lawn? | [4] |
| (c) If a piece of turf costs 50p, write down how much it will cost to turf the lawn. | [3] |
| (d) Grass seed is sold in boxes. Each box contains enough seed for 10 m2, and costs £5.15. Find the cost of sowing seed. | [5] |
| (e) Which method is cheaper? Why might your friends choose the more expensive method? | [3] |
Now look at the sample solutions and mark them as if you were the tutor. Finally, use the tutor's comments to assess your own solution and comments.
6.5.1 Another ‘making a lawn’ solution
Example 18 Making a lawn
Suppose you have some friends who are planning to put a new lawn in their garden. The lawn is to be 12 m by 14 m and they have a choice of either laying turf or sowing grass seed. You have been asked to help them decide between the two.
| (a) Write down the area of the lawn. | [3] |
| (b) The turf they can lay is sold in pieces, each of which is a square of grass measuring ½ m by ½ m. How many pieces of turf are needed to cover the lawn? | [4] |
| (c) If a piece of turf costs 50p, write down how much it will cost to turf the lawn. | [3] |
| (d) Grass seed is sold in boxes. Each box contains enough seed for 10 m2, and costs £5.15. Find the cost of sowing seed. | [5] |
| (e) Which method is cheaper? Why might your friends choose the more expensive method? | [3] |
Sample Solution B to Example 18
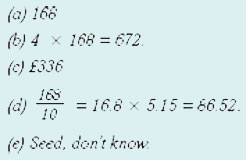
Click on ‘Reveal answer’ to see the tutor's marking.
7 OpenMark quiz
Hopefully, thinking about how your solution to a mathematical problem might be marked, will help you to produce better solutions for yourself, as well as for somebody else. Now try the quiz and see if there are any areas you need to work on.
Conclusion
This free course provided an introduction to studying Mathematics. It took you through a series of exercises designed to develop your approach to study and learning at a distance and helped to improve your confidence as an independent learner.
Acknowledgements
The content acknowledged below is Proprietary (see terms and conditions) and is used under licence.
Grateful acknowledgement is made to the following sources for permission to reproduce material in this course:
Course image: Tom Brown in Flickr made available under Creative Commons Attribution 2.0 Licence.
The content acknowledged below is Proprietary and is used under licence.
The following material is proprietary (and not subject to Creative Commons Licence) and used under licence (see terms and conditions):
Section 4.5: Sesame;
Section 5: Syndication International, Mirror Group Newspapers.
Don't miss out:
If reading this text has inspired you to learn more, you may be interested in joining the millions of people who discover our free learning resources and qualifications by visiting The Open University - www.open.edu/ openlearn/ free-courses
Copyright © 2016 The Open University










