Babylonian mathematics
Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Wednesday, 24 April 2024, 7:13 PM
Babylonian mathematics
Introduction
This course looks at Babylonian mathematics. You will learn how a series of discoveries have enabled historians to decipher stone tablets and study the various techniques the Babylonians used for problem-solving and teaching. The Babylonian problem-solving skills have been described as remarkable and scribes of the time received a training far in advance of anything available in medieval Christian Europe 3000 years later.
This OpenLearn course provides a sample of Level 2 study in Mathematics
Learning outcomes
After studying this course, you should be able to:
demonstrate knowledge about cuneiform and how it was used to represent numbers for mathematical problem solving and computation;
understand the relationship between a decimal place-value system and a sexagesimal one;
appreciate the advanced understanding of mathematics in Ancient Mesopotamia in relation to anyone in medieval Christian Europe 3000 years later.
1 Babylonian mathematics
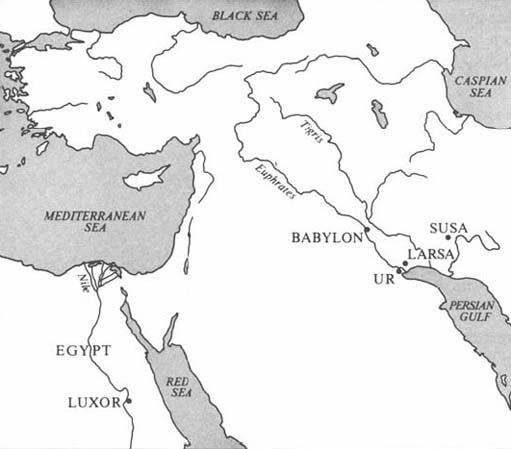
In Mesopotamia, the scribes of Babylon and the other big cities were impressing on clay tablets economic and administrative records, literary, religious and scientific works, word-lists, and mathematical problems and tables. Nearly all of the texts that give us our fullest understanding of Babylonian mathematics—indeed, of any mathematics before the Greeks—date from about 1800—1600 BC. During this period, King Hammurabi unified Mesopotamia out of a rabble of small city-states into an empire whose capital was Babylon, which was on the river Euphrates sixty miles south of present-day Baghdad. It is in this area, the valley of the two rivers Euphrates and Tigris which lead into the Persian Gulf, that there is the most ancient evidence for writing, some 1500–2000 years earlier still (see Figure 1).
By the middle of the third millennium BC, the writing style had evolved into the highly abstract and unrepresentational cuneiform (‘wedge-shaped’) script. This script, which was used initially for writing down words in the Sumerian language, was later also adopted by neighbouring peoples. All of the Babylonian tablets are written in Akkadian, a Semitic language quite different from Sumerian, although some mathematical tablets do use a few Sumerian words.
1.2 A Babylonian mathematical problem
Before seeing how our knowledge has been acquired, let us get into the spirit of things by ascertaining what a problem looks like once the modern cuneiform scholar has translated a tablet. The following example is taken from a tablet (see Figure 2), now at Yale University, translated by Otto Neugebauer and Abraham Sachs. Words in square brackets are their suggested reconstructions of what the tablet presumably says (where it is damaged), and words in parentheses are the translator's additions so that the English is (relatively!) more understandable.
I found a stone, (but) did not weigh it; (after) I subtracted one-seventh, added one-eleventh, (and) subtracted one-thir[teenth], I weighed (it): 1 ma-na. What was the origin(al weight) of the stone? [The origin(al weight)] of the stone was 1 ma-na, 9½ gin, (and) 2½ se.
This tablet contained 22 such problems-and-answers, none indicating how the answer was reached, and all involving a stone of 1 ma-na when weighed.
We can make little progress without knowing how the units of weight are related (there are in fact 60 gin to 1 ma-na, and 180 se to 1 gin), but it is possible to reach some conclusions from your experience.

Question 1
Do you think this is an actual practical problem? Have you seen anything like it before? Can you suggest what the tablet might have been for?
Discussion
It is clear this is not a practical problem—he would have done better to have weighed the stone when he found it, if he were really interested directly in its weight!
You probably noticed that it was formulated in terms of unit fractions. So, on the evidence of this tablet at least, similar things seem to have been taking place mathematically in Egypt and Babylon, at much the same time.
The facts that there are so many similar problems on the tablet and that no working is shown, both suggest that it may have been for teaching purposes in an oral teaching situation where the method was explained verbally. Just what was being taught is unclear, however, as several possibilities spring to mind: it could have been the method of solving problems like this; it could have been the learning of units of weight (for the solution comes out only if these are understood correctly). It could also have been a question of how to handle these unit fractions—notice that they are all awkward ones in that they do not divide into the weights (one-seventh of a ma-na does not come out as a whole number of gin or of se).
There is one further point that we should mention, in case you tried to work out the problem but could not obtain his answer. The fractions in the question are not all parts of the original stone, but are parts of whatever the previous step has been. So it is the stone less its seventh, plus the eleventh of that, and so on. This makes for a slightly more complicated calculation than most of the otherwise similar Rhind Papyrus problems that exist from this period in Egypt.
1.3 The historical study of cuneiform
Now, how did historical study reach the stage where Neugebauer and Sachs could pick up a tablet in a library and translate it so as to provide a fair degree of understanding? As with Egyptian hieroglyphs, cuneiform studies date from the last century. Their equivalent of the Rosetta Stone—a trilingual inscription for which one of the languages could be partially understood—was a sheer rock-face at Behistun in south-western Iran into which a text was carved in three languages, Old Persian, Elamite and Babylonian, proclaiming the victories of Darius the Great (520 BC). It was the British Consul in Baghdad, Henry Rawlinson, who rediscovered this inscription and between 1835 and 1851 copied it (at the risk to his life that any amateur mountaineer faces 300 feet up a precipice) and began to decipher both the script and the languages. Shortly thereafter, the burgeoning science of archaeology resulted in excavations of cuneiform tablets from ancient sites in Mesopotamia. These have sometimes been unearthed in vast quantities, with the result that there are now many more tablets available, in museums and universities throughout the world, than have been translated or even catalogued. It is only a small proportion of these that have been shown to have mathematical content, perhaps five hundred or so, compared with the several hundred thousand extant tablets. The results of studying these emerged in the 1920s and 1930s, and led to a considerable re-evaluation of the Babylonians, who within a decade changed from being a bare footnote to biblical studies (as in the Tower of Babel), to being a culture whose mathematical attainments put those of the Greeks of 1200 years later into a fresh perspective.
The earliest understanding to emerge was that of the Babylonians' remarkable numeration system. This discovery was due, once again, to Henry Rawlinson, who in 1855 was studying a tablet from the ancient city of Larsa. Look at the illustration and see if you can identify some of its main features, then come back to the description here.

It seems to consist of four columns, of which the second and fourth do not change, but the first and third do. The third, especially, changes in so regular a way that it is fair to infer that this is a column of successive numbers, constructed on a principle like that of the Egyptian hieroglyphic numbers. If ![]() represents 1, and
represents 1, and ![]() is 10, then the third column would be the numbers 49, 50,51,…, 58, 59, and then 1, for a reason that is not yet clear. The first column, though, is not so regular and has the curious feature that like symbols (if that is what they are) are not all collected together. The third line, for instance, has four 10s, then three 1s, then two 10s, then one 1. Rawlinson realised that all could be consistently explained if the assumption were dropped that a number sign could represent only one number value. So he suggested that the 1-symbol at the foot of the third column was to be understood as 60, and that the third line's first-column number was forty-three 60s and twenty-one 1s, This is, then, a place-value system (see Box 1), in which the value of each component number symbol depends on its place in the numeral as a whole.
is 10, then the third column would be the numbers 49, 50,51,…, 58, 59, and then 1, for a reason that is not yet clear. The first column, though, is not so regular and has the curious feature that like symbols (if that is what they are) are not all collected together. The third line, for instance, has four 10s, then three 1s, then two 10s, then one 1. Rawlinson realised that all could be consistently explained if the assumption were dropped that a number sign could represent only one number value. So he suggested that the 1-symbol at the foot of the third column was to be understood as 60, and that the third line's first-column number was forty-three 60s and twenty-one 1s, This is, then, a place-value system (see Box 1), in which the value of each component number symbol depends on its place in the numeral as a whole.
Box 1: A note on numeration systems
We write numerals in what is called the decimal place-value system: in ‘88’, for example, the first 8 has a value which is ten times that of the 8 in the units place.
We also have distinct symbols, 1,2,…, 9, 0, to put in each place without involving repetition; we have enough distinct symbols to avoid having to repeat ‘1’ eight times to signify 8, for instance.
The Babylonians had a numeration system as in A, except that it was sexagesimal—each place has value sixty times the next, compared with our ten times.
For constructing numbers within each place, the Babylonians used a repetitive system as with the Egyptian hieroglyphs. If there were no value in some place (which is what our zero symbol signifies) a space was sometimes left, but otherwise ![]() meant 1 or 60 or 3600 (or, indeed,
meant 1 or 60 or 3600 (or, indeed, ![]() or
or ![]() etc.) according to context. In much later sources, mainly astronomical texts dating from c. 300 BC onwards, a zero symbol
etc.) according to context. In much later sources, mainly astronomical texts dating from c. 300 BC onwards, a zero symbol ![]() is found to mark empty places within numerals; but not at the end of a numeral, so the absolute value of the whole is still left ‘floating’.
is found to mark empty places within numerals; but not at the end of a numeral, so the absolute value of the whole is still left ‘floating’.
Question 2
Try to transcribe the Larsa tablet. Can you suggest what the cuneiform words (columns two and four) might mean? (Hint: You may find that it helps to form some initial hypothesis about relationships among the numbers, and see if this is borne out elsewhere. So try first to work out the relationship of numbers in the second line (what relation does ‘forty-one sixties and forty’ have to fifty?), then see if the third line confirms this, and so to the whole tablet.)
Discussion
If you followed the hint, you should have found that
![]()
(forty-one sixties and forty) comes to 2500 in our numerals, which is the square of
![]()
(fifty). So we should try to see if this also works for other numbers. The next line we might hope would be the square of fifty-one, (that is, 2601), which indeed is forty-three sixties and twenty-one. It looks as though our hypothesis is on the right lines. Now we can go back to the first line, (which the hint steered you away from as it is slightly trickier), and note that if the first number is to be 49 squared (2401), then the cuneiform symbols cannot be forty-one anything—even though that is what they look like—but must be forty sixties and one unit.
It seems safe, then, to infer that column two carries the meaning ‘is’ or ‘equals’, and column four means ‘squared’, so the first line would read
2401 equals 49 squared
and so on, down to
3600 equals 60 squared.
There is one further thing to notice about our interpretation of the tablet. Suppose that all the numbers but one, say, had fitted our conjectured pattern: how should we respond to the inconsistent entry? It is just possible, number patterns being indefinitely many, that some other much more complicated interpretation could be found to cover every number without exception. Historians generally adopt the simpler view that the scribe must have made a mistake. Primary sources are not necessarily ‘correct’ merely by virtue of being old! Note that our confidence in sometimes changing the content of a tablet is only possible because of the mathematical structuring we presume it to have. Indeed, if a tablet is quite badly damaged it may be only that presumption that enables it to be reconstructed at all. (Perhaps this is a distinction between the history of mathematics and that of more empirical subjects.)
1.4 A remarkable numeration system
The Babylonian numeral system was described in Section 3 as ‘remarkable’. It is worth spelling out the reasons for this judgement. Although what we notice first is that it was a place-value system (see Box 1), what is perhaps more striking is the coupling of this feature with a ‘floating sexagesimal point’; that is, the lack of any indication about the absolute value of the number. This makes life hard for us in reading the tablets initially, but seems to have given the Babylonians unprecedented flexibility in calculations, because, among other things, there was no symbolic distinction between ‘whole numbers' and ‘fractions’. ![]() could be 30, or 1800 (=30×60), or ½ (=30×
could be 30, or 1800 (=30×60), or ½ (=30×![]() ), or
), or ![]() (=30×
(=30×![]() ), and so on. This approach completely sidesteps the relatively cumbersome Egyptian technique of handling fractional parts, and, together with the use of multiplication tables, leads arguably to computations even smoother than our own (at least before pocket calculators). We presume that, in any case where the absolute value of the number was significant, this would be clear to the scribe from the context. Also he would have needed to have kept his wits about him in doing addition or subtraction, where the places need to be lined up correctly. This system was used consistently only within mathematics, as far as we know. In dating, weights and measures, economic records and the like, there seems to have been a wide mixture of units with many local variations. (You saw an example earlier, in the ma-na to gin to se ratios of our first problem.)
), and so on. This approach completely sidesteps the relatively cumbersome Egyptian technique of handling fractional parts, and, together with the use of multiplication tables, leads arguably to computations even smoother than our own (at least before pocket calculators). We presume that, in any case where the absolute value of the number was significant, this would be clear to the scribe from the context. Also he would have needed to have kept his wits about him in doing addition or subtraction, where the places need to be lined up correctly. This system was used consistently only within mathematics, as far as we know. In dating, weights and measures, economic records and the like, there seems to have been a wide mixture of units with many local variations. (You saw an example earlier, in the ma-na to gin to se ratios of our first problem.)
It follows that there is a translation problem even in the task of finding equivalents in our system for what the Babylonian scribe wrote down. A helpful notation has been devised by Otto Neugebauer. He represents the value within each sexagesimal place in our numerals, separating the places by commas, (So the entries in the first column of the Larsa tablet would be transcribed as 40,1 41,40 43,21 and so on.) This leaves unspecified, just as the scribe did, the absolute value of a number. However, if we have reason to believe that we know where the ‘integer part’ of the number ends and the ‘fractional part’ begins, then a semi-colon is used to separate them. So, for instance, 1,10;30 would represent 60+10+30/60, which is 70½, or 70.5 in decimal fractions.
Now let us try this notation, and see more of the flexibility of Babylonian calculations. Below is an array of numbers from a different tablet, transcribed in Neugebauer's notation.
| 2 | 30 | 16 | 3,45 | 45 | 1,20 |
| 3 | 20 | 18 | 3,20 | 4X | 1,15 |
| 4 | 15 | 20 | 3 | 50 | 1,12 |
| 5 | 12 | 24 | 2,30 | 54 | 1,6,40 |
| 6 | 10 | 25 | 2,24 | 1 | |
| 8 | 7,30 | 27 | 2,13,20 | 1.4 | 56,15 |
| 9 | 6,40 | 30 | 2 | 1,12 | 50 |
| 10 | 6 | 32 | 1,52,30 | 1,15 | 48 |
| 12 | 5 | 36 | 1,40 | 1,20 | 45 |
| 5 | 4 | 40 | 1,30 | 1,21 | 44,26,40 |
Question 3
What do you think the table is about? (Hint: Try multiplying the paired numbers together and see if a pattern emerges.)
Observe that in the left-hand columns, certain numbers such as 7, 11, 13, etc. do not appear. Which ones are missing? Can you suggest a reason for this?
Discussion
Let us take line 6, and multiply 7,30 by 8. Now, depending on whether we take 7,30 to be 7;30 (=7½), or 0;7,30 (i.e. 7/60 + 30/3600, =450/3600, =0.125 in decimal fractions), or 7,30;0 (= 450), when we multiply by 8 we get 60, or 1, or 3600 respectively. But these are all represented by the same cuneiform symbol,
 , and so it does not matter which we choose. You can reach an identical conclusion by looking at any other pair. In short, the table shows numbers which multiply together to give 1 (say), so we could call it a reciprocal table. The numbers in the right-hand columns are, in effect, 1 divided by the left-hand numbers (and vice versa—notice, for instance ‘45 1,20’ at the top right, and then ‘1,20 45’ lower down the same column).
, and so it does not matter which we choose. You can reach an identical conclusion by looking at any other pair. In short, the table shows numbers which multiply together to give 1 (say), so we could call it a reciprocal table. The numbers in the right-hand columns are, in effect, 1 divided by the left-hand numbers (and vice versa—notice, for instance ‘45 1,20’ at the top right, and then ‘1,20 45’ lower down the same column).If you try to divide 7, 11 or 13 into 60, and to express the result in sexagesimal fractions, you will find that it does not work exactly; the process is never-ending. More generally, notice that the only numbers appearing in the table are ones which are the result of multiplying together 2s, 3s and 5s in various combinations, and that 2, 3 and 5 are the only prime factors of 60 (=2×2×3×5). Thus 50 (=2×5×5) is in the table, but 21 (=3 × 7) is not. It is an arithmetical fact that only numbers whose prime factors are 2, 3 and 5 have reciprocals which can be expressed as finite (i.e. terminating) sexagesimal fractions. Such numbers we will call, following Neugebauer, regular numbers.
There are a couple of further points to make at this stage. There is some debate among historians about whether this is to be interpreted as a table of reciprocals, as suggested above, or whether its function was as a conversion table of fractional parts into their sexagesimal equivalent. (So 2 would stand for the second part, 3 the third part, and so on down to 1,21 as the eighty-first part, in something like the Egyptian mode.) In this interpretation, the columns would be not of numbers related reciprocally, but of the same number expressed in two different ways, as a unit fraction and as a sexagesimal fraction. This is an attractive idea, illustrating once again that it is harder than we should like to identify definitively even simple-looking tables. Fortunately, for our purposes, we do not need to resolve this point, so we shall continue to refer to the table as a reciprocal table.
Secondly, the Babylonians were quite able to divide by numbers other than regular ones, and approximated the results to three or four sexagesimal places. There are reciprocal tables for complete sequences of numbers (i.e. containing both regular and non-regular ones) from the period. Any division problem, therefore, could be converted into an equivalent multiplication one by using such tables. In order to divide by a number, you multiply by its reciprocal. If the number you are trying to divide by is regular, then the answer will be exact; otherwise, it will be approximate, (Note that the Babylonians had more regular numbers in the above sense than we have—any number with prime factors other than 2 and 5 lands us with an unending decimal fraction: e.g. ⅓=0.333… .)
We have now seen how the Babylonian numerals work, and also two examples of tables, one of squares and one of reciprocals, which give an idea of the level, spirit and flexibility of Babylonian computations. We did not try to ascertain how the results on the tables were arrived at, as that seemed either obvious or not very interesting. But thus equipped, we are ready to tackle a table whose method of construction does turn out to be rather interesting.
1.5 Plimpton 322
1.5.1 Uncertain origins
The tablet is called Plimpton 322, and is described by Neugebauer (The Exact Sciences in Antiquity (Dover, 1969) p. 40) as ‘one of the most remarkable documents of Old-Babylonian mathematics’. The name arises simply from the fact that the tablet has catalogue number 322 in the George A. Plimpton collection at Columbia University, New York. Plimpton bought it in about 1923 from a Mr Banks who lived in Florida; it is not certain where he obtained it, but it may have been dug up at Larsa in Mesopotamia. The left hand side of the original tablet appears to have been broken off, and traces of modern glue suggest that this has happened since its excavation. (All of this is a fairly typical example of the random, not to say slapdash, way in which things have emerged from under the sand into the eventual light of public knowledge.)

Look at the photograph and notice the main features of what remains: four columns of numbers, with words at the head of each column. Now look at the transcription (we have labelled the columns A, B, C for ease of reference), and see if any pattern is evident to you
| A | B | C | |
|---|---|---|---|
| [1;59,0,]15 | 1,59 | 2,49 | 1 |
| [1;56,56,]58,14,5O,6,15 | 56,7 | 3,12,1 | 2 |
| [1;55,7,]41,15,33,45 | 1,16,41 | 1,50,49 | |
| [1;]5[3,1]0,29,32,52,16 | 3,31,49 | 5.9,1 | 4 |
| [1;]48,54,1,40 | 1,5 | 1,37 | 5 |
| [1;]47,6,41,40 | 5,19 | 8,1 | 6 |
| [1 ;]43,11,56,28,26.4O | 38,11 | 59,1 | 7 |
| [1;]41,33,45,14,3,45 | 13,19 | 20,49 | 8 |
| [1;]38,33,36,36 | 9,1 | 12,49 | 9 |
| 1;35,10,2,28,27,24,26,40 | 1,22,41 | 2,16,1 | 10 |
| 1 ;33,45 | 45 | 1,15 | 11 |
| 1;29,21,54,2,15 | 27,59 | 48,49 | 12 |
| [1;]27,0,3,45 | 7,12,1 | 4,49 | 13 |
| 1;25,48,51,35,6,40 | 29,31 | 53,49 | 14 |
| [1;]23.13,46,40 | 56 | 53 | 15 |
At first sight, this is not very promising! Something seems to be being listed, as the lines are numbered (final column); and the numbers in column A do diminish fairly regularly, from just under 2, down to just over 1⅓. (But if you did manage to notice that it was partly the effect of the editorially informed semi-coIons, and Neugebauer's reconstructions in square brackets, of course.) Otherwise, the numbers look fairly random, and there is little to tell that this is not a Babylonian supermarket till receipt. (Until Neugebauer studied the tablet, it was, in fact, catalogued as a ‘commercial account’.) But Neugebauer discovered—presumably after a considerable amount of conjecture and refutation—that the numbers in each line can be related as:
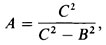
and this was the basis for his reconstruction of the illegible entries. Let us check this out on the simplest looking complete case, line 11.

So it is possible to find a relation, albeit a somewhat devious one, between the columns of the tablet. (In fact, for this to hold consistently throughout, the underlined numbers have to be considered as mistakes by the scribe, a point to which we shall return.) Before trying to decide what this is all about, let us investigate the numbers a little more. If we calculate C2−B2 for each entry, and then take its square root, something rather surprising emerges. Look at the next table, in which we have calculated the values (and the scribe's ‘errors’ have been corrected’). Ignore for the time being the final two columns which we have labeled p and q.
| B | C | p | q | ||
|---|---|---|---|---|---|
| (decimal) | (sexagesimal) | ||||
| 119 | 169 | 120 | 2,0 | 12 | 5 |
| 3367 | 4825 | 3456 | 57,36 | 64 | 27 |
| 4601 | 6649 | 4800 | 1,20,0 | 75 | 32 |
| 12709 | 18541 | 13500 | 3,45,0 | 125 | 54 |
| 65 | 97 | 72 | 1,12 | 9 | 4 |
| 319 | 481 | 360 | 6,0 | 20 | 9 |
| 2291 | 3541 | 2700 | 45,0 | 54 | 25 |
| 799 | 1249 | 960 | 16,0 | 32 | 15 |
| 481 | 769 | 600 | 10,0 | 25 | 12 |
| 4961 | 8161 | 6480 | 1,48,0 | 81 | 40 |
| 45 | 75 | 60 | 1,0 | ||
| 1679 | 2929 | 2400 | 40,0 | 48 | 25 |
| 161 | 289 | 240 | 4,0 | 15 | 8 |
| 1771 | 3229 | 2700 | 45,0 | 50 | 27 |
| 56 | 106 | 90 | 1,30 | 9 | 5 |
Notice that, compared wilh columns B and C, the values computed in D are remarkably simple looking numbers (this is particularly noticeable in their sexagesimal representation). You may indeed have recognised some as old friends, from the reciprocal table. In fact, all of them are regular numbers (whereas B and C are all, except for line 1L, non-regular), which explains why their squares could divide into C2 and yield an exact, finite sexagesimal expression.
1.5.2 What is the significance of the numbers?
In seeking the significance of these numbers, there is more information on the tablet that we have not yet taken into account, namely the text of the column headings themselves. The heading of column A is partly destroyed, but the text headings for B and C are clearer. B says something like ‘ib-sa of the front’, and C ‘ib-sa of the diagonal’, where ib-sa is a Sumerian word whose significance here is not precisely known. The geometrical cue provided by the headings suggests that we try viewing the numbers on the tablet as relating to geometrical figures. Indeed, as the numbers in the table above have the property B2+D2=C2 (which follows immediately from the way D was defined), it appears that the middle two columns of Plimpton 322 contain the shortest side and diagonal respectively of right-angled triangles, whose third side is a simple regular number. Successive lines in the table can then be seen to be ordered so that the triangles gradually change shape from B being almost equal to C, to it being rather shorter. (This is equivalent to what is shown in column A, where the ratio C2/D2 diminishes as one goes down the column—note that the actual numerical size of the triangles changes randomly, it is just the shape that varies in a smooth ordered way.)
We should think carefully about what these geometrical connotations of the numbers on the tablet might mean. We know from several other tablets that the Babylonians were well aware that adding the squares of the lengths of the two shorter sides of a right-angled triangle gives the same number as squaring the length of the diagonal (one version of the result that has come to be called, for no very sound historical reason, ‘Pythagoras' Theorem’). But why were whole number examples of such triangles listed on this tablet? (If that is indeed what the numbers signify.) Why ordered in this curious way? Why these particular triangles? What is the purpose of column A? The successful decipherment of Plimpton 322 has managed to raise rather more questions than when it was safely catalogued as a ‘commercial account’!
Historians have reached various conclusions about what this tablet signifies. Neugebauer and Sachs, the original decipherers, regarded it as ‘the oldest preserved document in ancient number theory’ and that it concerned ‘the fundamental laws of the numbers themselves’. (O. Neugebauer and A. Sachs, Mathematical Cuneiform Texts (American Oriental Society, 1945) pp. 37, 41.) So, on this interpretation, it has little to do with geometry as such, except incidentally, but more to do with properties of numbers. For what struck them especially, when trying to work out how the table had been constructed, was that each line can arise from a pair of small regular numbers (this is the significance of the columns labelled p and q in the table on the previous page). In fact,
B = p2 − q2; C = p2 + q2; D = 2pq,
as you can see by trying this out for yourself on any of the lines of the above table. So it is possible (no less, no more) that the Babylonian scribe was aware of these formulae though he would not, of course, have written them in anything like the modern algebraic form just given. These formulae generate Pythagorean triples, i.e. sets of whole numbers B, D, C, such that B2 + D2=C2. Was Plimpton 322 part of an investigation of number relationships?
It is evident, certainly, that the numbers on Plimpton 322 were the result of some mathematical procedure carried out off-stage, on another tablet perhaps. Apart from common-sense grounds, this can be inferred from the nature and occurrence of the errors on the tablet.
Question 4
Look again at the original translation of Plimpton 322, noting where the errors by the scribe were made. Are these compatible with column A having been calculated directly from columns B and C, as our ‘formula’ A=C2/(C2 – B2) might have tended to suggest?
Discussion
If column A had been calculated directly from columns B and C, then any mistake in B or C wouid carry over to A. But this has not happened, so A must have been calculated independently of B and C.
It is also worth noting that the scribe made four errors in computing the relatively simple B and C numbers, but none of consequence in the more complicated A column (there were in fact two minor confusions of place value, here ‘corrected’ in the transcription). As this is contrary to what one would expect, it seems a significant observation about the computations that went in to the tablet, even if it is not clear just what the significance is.
1.5.3 Errors in Plimpton 322
The presence of errors on the tablet is of further benefit to the historian, in that trying to discover how they could have arisen provides strong clues about how the computations were done. So, for instance, the last entry in column C is half what it ‘should’ be. The scribe wrote 53, where 1,46 is what is needed to preserve the pattern of the rest. This tells us that some stage in the computation must have involved a doubling or halving, which on this occasion the scribe overlooked.
Finally on this issue, it should be remarked that the very detection of ‘errors’ is bound up with the historian's analysis and understanding of the tablet. Although there is clearly an error somewhere along the bottom line, our pattern is equally preserved by taking it to be the column B entry that is in error, as double what it should be. This, however, disrupts the analysis in terms of generation by means of p,q pairs. The choice, then, between these two alternative errors depends on one's confidence that the Babylonian scribe was indeed generating the numbers on the tablet from something analogous to the formulae in terms of p and q given above.
Because of the tablet's evident importance, many historians have considered this question. Not all historians have followed Neugebauer and Sachs in their interpretation of Plimpton 322 as an investigation of number theory. An interesting suggestion has been put forward by Jöran Friberg, who argues that the tablet was a ‘teacher's aid’ for setting and solving problems involving right-angled triangles. So, for example, if the teacher wanted to set a problem like, ‘a ladder of length C leans against a wall, its base is distance B from the wall, how high up the wall does it reach?’. Then choosing the numbers B and C from the Plimpton tablet would ensure that the answer (D) would come out nicely, and not leave the poor student with an unending sexagesimal fraction to cope with. We have no space here to investigate Friberg's justification for this view, but it does sound plausible, especially because it is attentive to the situation in which we believe the tablets to have been produced and used. Please read the short extract from Friberg attached as a pdf. We shall then move on to consider this wider aspect of the social context of Babylonian mathematical activity.
1.6 The social context of Babylonian mathematical activity
The extant mathematical tablets from the Old Babylonian period fall broadly into two categories, table texts and problem texts. You have seen examples of both of these. The weighing-the-stone problem with which we started is from a problem text, while all the others—the table of squares, the reciprocal table and Plimpton 322—are table texts, tablets consisting solely of tables of numbers. Several hundred table texts have been found, and many types of calculations appear to have been carried out by means of them. As well as squares and reciprocals, there are multiplication tables, tables of cubes and cube roots, tables of the sums of squares and cubes, combined tables where several of these are present, tables for working out compound interest, tables of weights and measures, and others. Numerical tables seem to have been a staple constituent of Babylonian life, as ubiquitous for them as is the pocket calculator for us today. Problem texts, by contrast, are rarer—only a hundred or so tablets have been found—and they seem to relate to an educational context of advanced scribal training. Early Mesopotamian culture had seen the development of specialised occupations, as a part of the newly-developing and highly-complex urban structuring of the community, and the profession of scribe was central to the running of economic, bureaucratic and other aspects of the state. There were special institutions, schools, for training future scribes in the arts of writing, counting and accounting, and other necessary skills. (The attached pdf affords revealing glimpses into the scribal art and its training.)
It is in this educational context that the problem texts seem to have been written and used. Some merely give the problem and the answer (the one you saw in Question 1 was of this sort); others are fortunately more forthcoming on what to do to reach the answer. Let us look at one of these now.
Please read through the extract below to gain an impression of its style.
I have subtracted the side of my square for the area: 14, 30. You write down 1, the coefficient. You break off half of 1. 0; 30 and 0; 30 you multiply. You add 0; 15 to 14, 30. Result 14, 30; 15. This is the square of 29; 30. You add 0; 30, which you multiplied, to 29; 30. Result 30, the side of the square.
The problem is given in the first sentence, the rest is its solution. It turns out that after doing various things to the numbers initially given, the result 30 is reached. This indeed solves the original problem, for a square of side 30 has area 302 = 900 (= 15,0 in sexagesimal), and subtracting 30 from 900 gives 870 (= 14,30). This is a problem of the kind we would call quadratic, that is, involving the square of some unknown number which is to be found. As a way in to understanding the Babylonian computational procedure for this problem, let us follow the instructions through in a modern algebraic format (and take into account later how far this may have distorted the Babylonian scribe's activity).
Let us call the unknown, the side, ‘x’; the coefficient, (which here is 1), call ‘b’; and the number in the statement of the problem (here, 14,30) call ‘c’. Then the problem is; to find x, where x2 − bx = c. The solution consists of taking the coefficient b, halving it, ½b squaring that, (½b)2; adding this to the result, c+(½b)2; taking the square root of that, √(c + (½b)2); and finally adding the result to the halved coefficient ½b + √(c + (½b)2); which is the answer. Indeed, this algebraic formula is just the same as we would reach (see Box 2 below), which is most satisfactory—or perhaps, on another consideration, somewhat alarming. If our method of understanding what the Babylonian scribe might have been doing is to turn him into a twentieth-century algebraist, it is possible that there has been some misunderstanding.

Box 2: A note on solving quadratic equations
If we have a quadratic equation (a problem with one unknown, involving the square of that unknown but no higher power) in its standard form
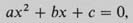
then we find a solution by putting the values given for a, b and c inlo the formula
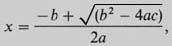
which can be obtained from the standard form of the original equation through a succession of algebraic operations called completing the square.
In the particular case of a quadratic equation of the form
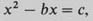
into which the problem specified on the tablet fits, the procedure of completing the square goes as follows.
Take the coefficient b; halve it (½b); square that and then add it to both sides:
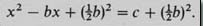
Then the left hand side is the square of (x − 1/2b that is,
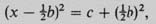
so take the square root of both sides, giving
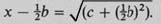
Finally, add ½b to both sides to give
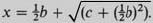
Question 5
How does the symbolic description given above compare with what the Babylonian scribe did? Approach this by considering separately: (i) what similarities there are, and (ii) what differences there are.
Discussion
The sequence of instructions given by the scribe seems to follow quite closely the procedure called (in Box 2) completing the square, in terms of actions on theparticular numbers specified at the outset.
You may have noticed another similarity if you pondered the way in which the Babylonian problem was formulated. As with the stone of Question 1, the scribe seems to be labelling the unknown in an abstract, symbolic way. To see this, consider the alternative possibility that this is a realistically geometrical problem, as the words side and area seem, on the face of it, to imply. Surely the formulation of taking a side away from an area does not really make sense 10 our way of thinking about geometry (apart from conjuring up imagery of farmers ploughing up hedgerows). They are different kinds of things–taking away a hedge does not alter the numerical measure of the area that was previously enclosed. So either Babylonian geometry was quite different from ours, or they were using the terms side and area not as meaning geometrical entities particularly, but more as unknown and square of the unknown. In other words, side referred to some number to be discovered, with no connotations of where it came from or what, if anything, it measured. This is similar, perhaps, to the way we speak of x squared without necessarily imagining a square.
I expect you observed that there are major notational differences. It is worth noting that these are of three sorts: our ‘x’ for unknown, our ‘b’ and ‘c’ for fixed numbers, where we do not want to be specific about what they are, and all the other symbols (+, √, =, and so on). The latter seem fairly harmless translations of Babylonian words and operations in this case.
It has been argued above that our x and their side are conceptually more similar than they may first sight. But in changing their numbers into our ‘b’ and ‘c’ we effected a rather dramatic conceptual change. There is nothing in the Babylonian text paralleling our formula, a structure in which all the contributions of the original coefficients are still evident.
But bear in mind that our ‘formula’ only makes sense through our understanding the conventions about the order in which the operations it embodies are to be performed. Given a formula like √(c + (½b)2), we are taught to interpret it as, ‘square ½b, then add c, before taking the square root…’, which is beginning to sound like Babylonian instructions again. Indeed, the parallel is all the more marked in the computational techniques developed over the last couple of decades Solving a quadratic equation on a pocket calculator or computer involves carrying out a sequenced program of operations closely mirroring the instructions on the Babylonian tablet, even down to pushing the ‘square root’ button at just the stage the scribe would have leant over to consult his square root tables.
All the problem texts that have solutions are of this sort, apparently instructing about a general approach through particular instances. In some cases, all the answers on a particular tablet turn out to be the same, which seems a clear indication that it was the journey rather than the destination that mattered. This is confirmed by details within the calculations. For instance, sometimes a number is explicitly multiplied by 1, which seems pointless until one realises that, in general, it might be some number other than 1 at that stage. This serves as a reminder that some multiplication is to be done there.
1.7 Babylonian mathematical style
Not only should you have learnt through this exercise more about the Babylonian mathematical style, but also, on another level, you should have gained more experience in the endeavour of trying to understand past mathematics. The model that we have been trying out can be characterised thus: use any means, any symbolism or notation that occurs to you, to find your way into the problem, then check rigorously to see how much of your new understanding is more a projection backwards from your own time and techniques. First, try to understand what they might have been doing. Then address the harder questions of how and why. As this process becomes more familiar, you will find it increasingly easy both to respond to past mathematics on its own terms, and to understand and evaluate historical questions and concerns. (Doing this may also produce the added bonus of a better understanding of your own mathematics.)

The Babylonian ‘quadratic’ problem above is fairly characteristic of problem texts; some have two unknowns (length and width) and two conditions connecting them, and a few even have three unknowns and three conditions. Some involve cubes or higher powers of unknown numbers which are to be found. The problems are expressed sometimes fairly abstractly, as we have seen, sometimes in terms of more concrete imagery that seems direct training for practical problems which a scribe might be called upon to solve professionally. (See, for example, the collection of problems in the attached pdf concerning a number of workers digging a volume of earth for so many days at a certain expected productivity.) Yet even apparently practical problems can have flamboyantly unrealistic solutions—on one tablet (see the attched pdf), the problem is to discover what area of field can be irrigated by a particular volume of water, and the answer turns out to be a field some 3½ kilometres square, covered with water to a uniform depth of one finger's breadth, a procedure that would tax even the most diligent of Babylonian farmers!
Conclusion
In conclusion, what is Babylonian mathematics about? Although it is not easy to answer this question precisely, because of the difficulties of interpretation such as you saw with Plimpton 322, the overwhelming impression is of the study and use of numbers, and various techniques for solving problems involving numbers. Where the numbers arise from—whether land measurement, economic questions, idealised geometrical objects (cubes, triangles and so on), or just fairly abstractly—seems a relatively secondary matter. As Otto Neugebauer has put it:
The central problem in the early development of mathematics lies in the numerical determination of the solution which satisfies certain conditions. At this level there is no essential difference between the division of a sum of money according to certain rules and the division of a field of given size into, say, parts of equal area.
O. Neugebauer, The Exact Sciences in Antiquity pp. 44–5.
The Babylonian problem-solving skills, as we infer them from the problem texts, were remarkable. The Babylonian scribe, for example, received a training in these matters far in advance of anyone in medieval Christian Europe 3000 years later. The Old Babylonian knowledge was preserved somehow through all the alarums and excursions of subsequent Mesopotamian history, and filtered through in some measure to the later Alexandrian Greeks. Just what knowledge, however, and when, is not precisely known at present.
Babylonian techniques are sometimes described as algebraic, although other historians would reject the applicability of the term. You can begin to see that the style of mathematics used in some culture or period can be a better way of trying to understand and empathise with past mathematical activity than is the desire to fit topics of concern into pre-ordained slots. For, as we have already seen, the ostensible subject matter, the language used, and the techniques applied do not always fit together in past cultures in the way they do in ours. It is some combination of all these things that is characterised by the word style.
Further reading
Acknowledgements
The content acknowledged below is Proprietary (see terms and conditions) and is used under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Licence.
Course image: dynamosquito in Flickr made available under Creative Commons Attribution-ShareAlike 2.0 Licence.
All other materials included in this course are derived from content originated at the Open University.
Don't miss out:
If reading this text has inspired you to learn more, you may be interested in joining the millions of people who discover our free learning resources and qualifications by visiting The Open University - www.open.edu/ openlearn/ free-courses
Copyright © 2016 The Open University