Visualisation: Visual representations of data and information
Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Friday, 26 April 2024, 9:48 PM
Visualisation: Visual representations of data and information
Introduction
How many times a day do you hear it said that we are drowning in a sea of information? As the cost of computer data storage goes down, it becomes easier and cheaper to store ever more data about ever more things, from corporate information to personal data – yet how are we ever to make sense of all this data and uncover some of the potentially valuable information it contains?
Visualisation can help. This is because, of all the human senses, the visual sense is one of the most powerful. In this course, you will learn how to interpret, and in some cases create, visual representations of data and information that display a wide range of data sets in a meaningful way.
This OpenLearn course provides a sample of level 2 study in Computing & IT
Learning outcomes
After studying this course, you should be able to:
understand what is meant by the term ‘visualisation’ within the context of data and information
interpret and create a range of visual representations of data and information
recognise a range of visualisation models such as cartograms, choropleth maps and hyperbolic trees
select an appropriate visualisation model to represent a given data set
recognise when visualisations are presenting information in a misleading way.
1 Before you begin your study
During the course of this course, your study will involve following links to external websites and resources. In places the material is open-ended in what it asks you to do. In addition, there are several optional activities that may interest you at the end of this part to allow you to explore this topic in more detail. Aim to spend about eight hours in total on the core material.
In places the material relies on your exploring a variety of online active tools for yourself. Some of the suggested tools may require you to register for an account. If you do register a new account on these services, take care not to share personal information you are uncomfortable with sharing, and do not reuse a password that you use elsewhere.
If a service requires an email verification before you can use the service, you could if you wish use a disposable email address (search for ‘disposable email address’ using your favourite search engine). These email addresses last long enough for you to pick up an email that is sent to them immediately, but then they disappear. Note that if you register with a service using a disposable email address and want to reuse that service at a later date, it will not be able to email you a replacement password if you have forgotten the one you originally registered with.
If a service asks for a date of birth for no particularly good reason, you could if you wish invent a ‘web birthday’ for yourself: a date you can remember that is not your real birthday.
1.1 An introduction to visualisation
Activity 1 (exploratory)
Before you go any further, watch the following video presentation by Hans Rosling, Professor of International Health at Sweden’s Karolinska Institute.
It lasts about 20 minutes, and will show you very clearly just how powerful visualisation can be.
If you are reading this course as an ebook, you can access this video here: The Best Stats You've Ever Seen | Hans Rosling | TED Talks
Comment
We’ll come back to the software Rosling used in his visualisations later on, but first we need to think a little more about visualisation: what it is, what it can do for us and what sorts of visualisations are used and useful.
Visualisation is a process whereby data is represented in a graphical way in order to expose patterns and relationships that might otherwise be missed. If you look at a list of unordered numbers, such as the number of mobile calls per subscriber in a particular country over time, you may be able to spot a general increase in the number over that time interval just by casting your eye over the list of numbers. However, it is unlikely that you would spot more ‘elaborate’ trends in the data, such as variations with the time of year, say. Or if you are given a list of numerical GPS co-ordinates, you would probably find it hard to work out the route that was actually taken, just from the list of numbers. Visualisation can bring those numbers alive, and make those periodic trends, as well as the path taken on a GPS journey, self-evident.
Activity 2 (exploratory)
Every so often, the Office of National Statistics (ONS) surveys a sample of UK households about, among other things, their use of the internet (Office for National Statistics, 2010). Skim through this ONS report on domestic internet access for 2010, looking at the range of data tables it contains. As you do so, think about what sort of technique(s) might be appropriate to display the data shown in the various tables in a graphical way.
Comment
You might like to return to this activity at the end of this free course and see to what extent you would want to change your answer as a result of what you have learned.
As a discipline, visualisation is rapidly evolving: more and more online and offline applications that are capable of visualising data from data sharing applications such as online spreadsheets, databases and general ‘data repositories’ are providing ever easier ways to visualise data ‘for free’. In the corporate world, so-called ‘enterprise mashup’ services offer ways of exposing business data to users who can then visualise it for a particular purpose, or to answer a particular question. Just as search engines like Google made it easier to search the web and discover relevant answers to particular search queries, so visualisation techniques are providing ever more powerful ways of interrogating data and getting answers from it.
Visual representations can also be misleading, though, and should be treated with caution, as should the data that underpins them. So let’s make a start by looking at some very common visualisation techniques, in the form of the most popular spreadsheet chart types, as well as seeing how not to present them.
2 The most common spreadsheet charts
In this section, I’m assuming that you are familiar with three types of charts provided by spreadsheets – bar charts, pie charts, and line charts (often referred to as ‘line graphs’ or just ‘graphs’) – and know how to use a spreadsheet to produce them.
Types of charts
Each chart type communicates information differently to the chart reader. (Or should that be ‘chart viewer’? The terms will be used interchangeably.)
- The pie chart, as shown in Figure 1(a) below, can be used to represent proportions of a whole. For example, if you have set of non-overlapping, percentage-based results that add up to 100%, and not too many categories, it might be appropriate to use a pie chart to represent the results in a visual way.
- The bar chart, as shown in Figure 1(b) below, can be used to compare data obtained from independent members of a set, such as the population size for each country in the set of countries in the European Union.
- The line chart, as shown in Figure 1(c) below, is often used to plot the behaviour of a numerical quantity over time (in which case the data may be described as ‘time-series data’). More generally, line charts can be used to plot two continuous variables against each other.
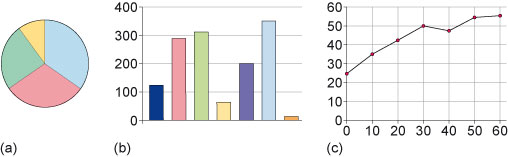
This figure has 3 parts. Part (a) shows a circle divided into sectors of varying sizes. Each sector (pie slice) is filled in a different colour. Part (b) shows a bar chart with vertical bars. The axes are not labelled and there are no units. The vertical axis has a scale from 0 to 400 with equal divisions at intervals of 100. Seven vertical bars are shown, each a different colour and height. Part (c) shows a line chart with a set of axes that have no labels or units. The horizontal and vertical axes are both marked at intervals of 10 from 0 to 60. Various points are marked dots on the graph and these are joined by a straight line between each dot which results in a generally rising line.
Activity 3 (self-assessment)
Which chart type would you choose for each of the following data sets?
- a.The number of mobile phone minutes called in the UK recorded on a monthly basis over the last year.
- b.The number of mobile phone subscribers in the UK recorded on a monthly basis over the last year.
- c.The number of mobile phone subscribers in the UK recorded on a monthly basis over the last five years, with the purpose of revealing the trend and making a forecast for the next three years.
- d.The relative market share in terms of subscribers of the different mobile phone operators.
Comment
Here are my answers, with reasons.
- a.A bar chart would be an appropriate way of displaying this information, on the assumption that usage in one month is independent of usage in another month.
- b.Although you could use a bar chart here, a line chart would be more appropriate, because a significant number of subscribers in one month are likely to be continuing subscribers from a previous month and so the number of subscribers in one month is not really independent of the number in the previous month.
- c.Line charts are the best adapted to revealing trends and making forecasts, so a line chart would be most suitable here.
- d.As we are talking about proportional market share – that is, the share of the whole market held by each company – it would make sense to use a pie chart to display this information, using separate segments for not more than the four or five dominant providers and a single ‘other’ segment to represent the rest.
3 Cheating with charts
One of the reasons for using visualisation is that it allows us to ‘see’ what is going on in a data set, by providing a shorthand ‘at-a-glance’ way of exposing patterns or distributions, where the patterns or trends are graphically self-evident. However, depending on the visual context the data is provided in, the visualisation can sometimes be misleading. In this section, you’ll see a few ways in which graphical representations – specifically line charts, bar charts and pie charts – may be deliberately or carelessly misleading, and do more harm than good in the sense of miscommunicating information rather than failing to communicate it at all.
Before we get started, though, familiarise yourself with the range of ways in which people currently use bar charts, line charts and pie charts by trying the following activity.
Activity 4 (exploratory)
Try the following image searches on Google Images, or an image search engine of your choice:
first, “bar chart” on Google Images
next, “line chart” on Google Images
and finally, “pie chart” on Google Images.
For each chart type, do the charts look broadly the same? What sort of variety is possible in the display of each chart type?
Comment
You may have been struck by how much variation there was in the use of colour and detail on the charts. You probably found that the quality and extent of labelling on the axes varied widely. You may also have found that some charts attempted to use 3D effects which looked pretty at first glance, but at a second look may have become quite distracting and even hard to read.
3.1 Cheating with line charts
Line charts are often used to display the values of particular quantities, such as share prices, or sales figures, over a period of time. Such data is sometimes called time-series data. In this section, you will see various ways in which time-series data and other time-ordered data can be charted and explored in a graphical way.
In order for the line chart to be meaningful, the origin of the graph – that is, the value on the vertical axis where it is crossed by the horizontal axis – is often chosen so that the variation in the quantity being graphed fills the chart. This is particularly the case where the range of the charted values (that is, the difference between the highest and lowest values) is much smaller than the magnitude of the values themselves. So, for example, in the chart in Figure 2 taken from Yahoo! (Yahoo! UK & Ireland, 2009) we see the value for the Barclays Bank share price in late 2008 and early 2009. The minimum price shown is around the 130 mark, and the maximum is nearly 190, so it makes sense to use a range on the vertical axis that is just a little larger than this.
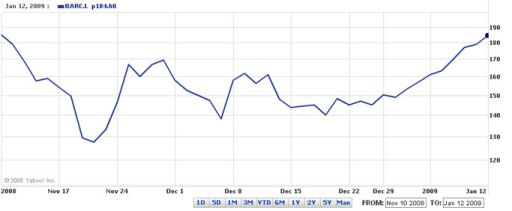
This line graph shows how Barclays Bank share price changed with time. The horizontal axis is labelled ‘From Nov 10 2008 to Jan 12 2009’ and is marked in units of date, from November 2008 to 12 January 2009, at intervals of 1 week. The vertical axis is not labelled and is marked in units of share price, from 110 to 190, at intervals of 10.The divisions on the vertical axis are gradually and evenly getting smaller as the share price increases up the vertical axis. The line is a series of short straight lines joined to form a continuous line. It starts at just below 190 for 10 November and falls to a low of around 130 between 17 November and 24 November. After that the line rises in a series of peaks back to nearly 190 on 12 January.
If you compare the two charts shown in Figure 3 for two different periods in 2008, you should notice that the automatically displayed range of values on the vertical axis is different in each case. If you don’t take care looking at the values on the vertical axes, you may fail to appreciate the difference in performance. You also need to be alert to the fact that the vertical scale in both charts is non-linear. This is particularly noticeable in the August to September chart on the bottom: the distance on the chart between the 440 and 460 lines is less than the distance between the 280 and 300 lines.
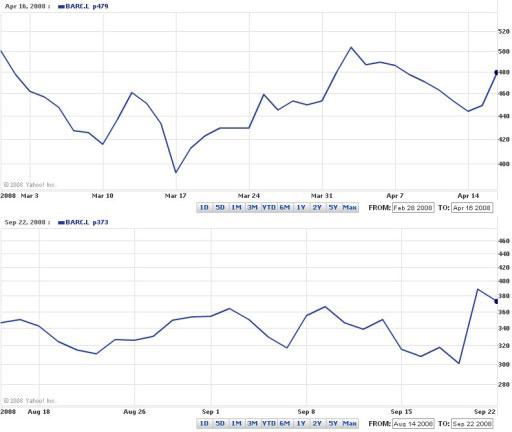
In this figure there are 2 line charts. Both charts show how Barclays Bank share prices changed with time but over different time periods. The charts have different axes and scales.
The top chart: The horizontal axis is labelled ‘From Feb 28 2008 to Apr 16 2008’ and is marked in units of date, from a short time before 3 March to shortly after 14 April, at intervals of 1 week. The vertical axis is not labelled and is marked in units of share price, from 390 to 520, at intervals of 20.The divisions on the vertical axis are evenly spaced.
The line is a series of short straight lines joined to form a continuous line. It starts at 500 on 28 February and falls to just under 420 by 10 March. After that a sharp peak rises to 460 mid-week and then falls back to below 400 by 17 March. From then the share price rises steadily with two small peaks to mid-week 31 March after which it gradually drops until 14 April before rising again towards the end of the period.
The bottom chart: The horizontal axis is labelled ‘From Aug 14 2008 to Sep 22 2008’ and is marked in units of date, from a short time before 18 August to 22 September, at intervals of 1 week. The vertical axis is not labelled and is marked in units of share price, from 260 to 460, at intervals of 20. The divisions on the vertical axis are gradually and evenly getting smaller as the share price increases up the vertical axis.
The line is a series of short straight lines joined to form a continuous line. It starts at 350 on 14 August and falls to just under 320 by 21 August. After that it rises steadily to 360 after 1 September and then falls back sharply to below 320 by 7 September. From then, after a sharp rise, the share price rises and falls with a general downwards trend to mid week after 15 September, after which it rises sharply towards the end of the period.
The effect of the non-linear scale is even more marked if we look at the chart in Figure 4, which is over the period September 2008 to January 2009: the horizontal lines are very much closer together near the top of the graph than they are near the bottom. But is a non-linear scale like this misleading for a quantity like share prices?
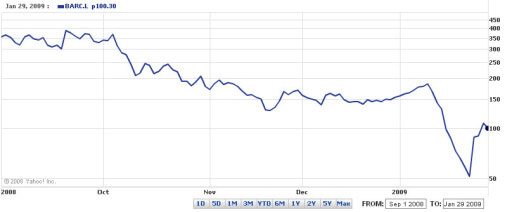
This line graph shows how Barclays Bank share price changed with time. The horizontal axis is labelled ‘From Sep 1 2008 to Jan 29 2009’ and is marked in units of date, from September 2008 to January 2009, at intervals of 1 month. The vertical axis is not labelled and is marked in units of share price, from 50 to 450, at intervals of 50.The divisions on the vertical axis are gradually and evenly getting smaller as the share price increases up the vertical axis.
The line is a series of short straight lines joined to form a continuous line. It starts at just above 350 for September and shows a downward trend but with some sharp drops and other times when the line is horizontal or rises slightly. 2 sharper drops stand out. Between early to mid-October the price drops from 350 to 200 (approximately) where the length of the graph line showing this drop is 1.5 centimetres. Secondly between mid to end January the price drops from 200 to 50 (approximately) where the length of the graph line showing this drop is 3 centimetres.
Activity 5 (exploratory)
Looking at Figure 4, which appears more dramatic: the (approximately) 150 pence drop in early October 2008, or the (approximately) 150 pence drop in January 2009?
Is the non-linear vertical axis misleading? To answer this, find the approximate percentage change in share value in each case.
Comment
The later drop appears far more dramatic. In October the drop was about 150 pence from a starting point of around 350 pence, which is approximately 40%, whereas in January the drop was about 150 pence from a starting point of around 200 pence, which is approximately 75%. So the January fall not only looks more dramatic on the chart, but is more dramatic. The non-linear vertical axis is therefore not misleading, instead it has helped us to visualise the relative severity of the two falls in price.
Activity 6 (exploratory)
Using an interactive line chart, explore a range of time-series data values over different time periods. By selectively choosing different periods of time, can you create different views of the time-series data that appear to tell a different story from the one that is being told when you look at the data over a longer time period. If the website will permit it, also change the origin (that is, the point at which the horizontal axis crosses the vertical axis).
Comment
You probably discovered from your exploration that changing the period of time and changing where the axes cross can create graphs that give very different impressions.
Activity 7 (self-assessment)
For a price varying between 10,000 and 10,250, how might you produce a line chart that at first glance makes it appear as if:
- the value is not changing much at all;
- the value is changing wildly?
Comment
- a.Set the range of the vertical axis range to be 0 to 11,000;
- b.Set the range of the vertical axis range to be 9900 to 10,300.
It is frequently the case that several data series collected over the same period of time will be displayed on the same chart, often using a different colour for the different data series. In such cases, the vertical axis scale may or may not be the same for each data series.
It’s worth bearing in mind that if a time-series data plot is actually an average of two or more related data sets, it may well tell a misleading story. For example, the plot in Figure 5 of Google search trend data suggests that searches for ‘flowers’ are popular three times in the first half of the year.
Or maybe not? See also Figure 6.
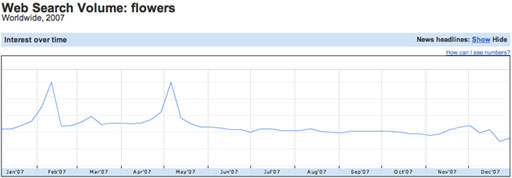
This line graph shows how the number of Google searches for the word ‘flowers’ changes with month of the year. The horizontal axis has no label and is marked in units of date, from Jan 07 to Dec 07, at intervals of 1 month. The vertical axis is not labelled and has no units or scale. The line is roughly horizontal with 2 large and 1 small sharp peaks. The large peaks occur in mid February and early May and the small peak in mid March.
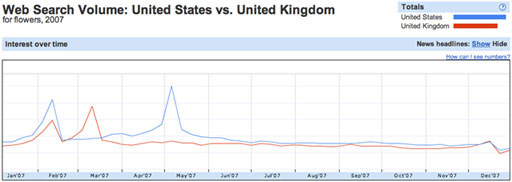
This line graph shows how the number of Google searches for the word ‘flowers’ changes with month of the year. There are 2 lines shown: a blue line for United States data and a red line for United Kingdom data. The axes are the same as for Figure 5. Both lines are roughly horizontal, each with 2 sharp peaks. The blue line has 2 large peaks in February and May. These coincide with the 2 large peaks in Figure 5. The red line has a smallish peak coinciding with the February large peak of the US figures. The red line also has a larger peak coinciding with the small peak in early May in Figure 5.
In Figure 6, which shows the search trends for ‘flowers’ in the UK and the USA separately, we see that peaks in search volumes may be localised to particular countries. Here, Valentine’s day is common to both countries, but Mother’s day is celebrated at different times of year.
There is some optional material on time-series data in section 9.1.
3.2 Cheating with bar charts
Bar charts are subject to various sorts of ‘creative’ use. For example, the bar chart in Figure 7 shows huge differences in the four charted quantities, does it not?
Or maybe not – see also Figure 8.
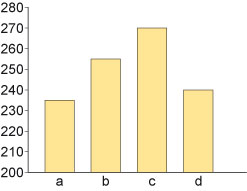
This vertical bar chart has 4 columns of varying height. The horizontal axis has no label and just shows each column labelled with a, b, c and d from left to right. The vertical axis is not labelled and has no units, but the scale goes from 200 to 280 in divisions of 10. The heights of the columns cannot be read accurately but are at approximately the following heights on the vertical axis:
- a 235
- b 255
- c 270
- d 240
The overall impression is of quite large variation in bar heights.
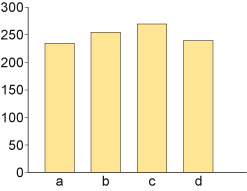
This vertical bar chart has 4 columns of varying height. The horizontal axis has no label and just shows each column labelled with a, b, c and d from left to right. The vertical axis is not labelled and has no units, but the scale goes from 0 to 300 in divisions of 50. The heights of the columns cannot be read accurately but are at approximately the following heights on the vertical axis:
- a 235
- b 255
- c 270
- d 240
The overall impression is of quite small variation in bar heights.
Many spreadsheet packages that are used to create charts also allow the user to employ shapes other than simple bars when constructing a bar chart. This may not be a good thing.
For example, chart widgets like the ones shown in Figure 9 are available from Google Charts. As well as being potentially misleading because it’s not immediately clear where zero lies (the train chart ranges from 200 to 270 whereas the piles of money chart ranges from 0 to 270), the imagery can also be a distraction. Where different 2D shapes are used for the bars, the area of the shape may change out of proportion with the height or length of the ‘bars’, which would mislead the reader at a perceptual level. Where 3D imagery is used, the reader can be confused (even unconsciously) about whether the height or the volume of the chart is what is significant.
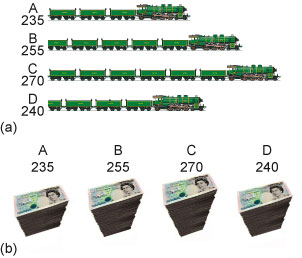
This figure shows 2 charts designed with images of real items representing the columns.
Chart (a) is similar to a horizontal bar chart. Each bar consists of a train locomotive and some carriages. Each bar has a label showing its length (although there are no scales). From the top the lengths are:
- A 235
- B 255
- C 270
- D 240
Chart (b) simply shows some piles of money (notes). Although differences in height of the money piles can be noted it is only possible to make very rough judgements about their relative heights. The piles are labelled from left to right:
- A 235
- B 255
- C 270
- D 240
3.3 Cheating with pie charts
Pie charts are some of the most commonly found graphical devices, although they can be difficult to read and are often misleading. (Several commentators suggest they are always misleading, and that, because they only make visual sense for visualising small data sets, it is often better just to use a numerical table.)
So what actually are they used for? Pie charts are charts that are used to represent the distribution of ‘proportions of a whole’. For example, if you conduct a survey of 100 people, you might use a pie chart to display how they answered a question of the form ‘choose only and exactly one item from the following list’, such as ‘which brand did you buy in your most recent purchase of a mobile phone?’ However, if you then went on to ask an optional, ‘yes/no’ question that only 27 of the 100 people were prepared to answer, representing the results from just those respondents in a pie chart would potentially be misleading – a reader might assume that the results applied to the whole survey population of 100. So in that case it might be better to show a chart with three sectors – one for ‘yes’, one for ‘no’, and one for ‘did not answer’.
Changing the size of the whole referred to in different charts in the same report is one way of potentially misleading the reader of a report. But it is also possible to mislead readers in their perception of a single chart. For example, in the pie charts in Figure 10, which sport has the biggest proportion? Which has the smallest?
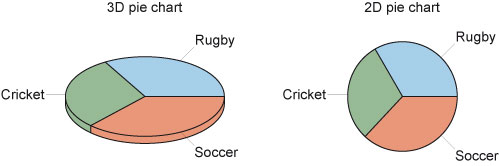
This figure shows 2 pie charts each divided into 3 sectors of red, blue and green. On both charts the red sector at bottom right is labelled ‘Soccer’, the blue sector at top right is labelled ‘Rugby’ and the green sector at left is labelled ‘Cricket’. The left-hand pie chart is labelled ‘3D pie chart’ and has the appearance of a coin lying on a table where you can distinguish the top of the coin and the front edge. The right-hand pie chart is labelled ‘2D pie chart’ and has the appearance of a coin standing on edge on a table where only the front face can be distinguished. In the 3D chart the sectors for Rugby and soccer seem very similar in size and cricket appears smaller. In the 2D chart all the sectors appear very similarly sized.
The actual distributions are: soccer 100, rugby 90 and cricket 80 (in a situation where 270 people were asked to choose their favourite among these three sports). In this case, the 3D chart does manage to suggest this, although the differences are harder to spot than in the 2D chart. However, it is also possible to orientate the 3D chart so as to make one sector appear larger or smaller than another, similarly sized one. And colour can also have an effect on how we perceive the relative sizes. A full consideration of the perceptual effects that can be exploited to highlight particular results (or even to attempt to mislead a reader) when designing a chart will not be given here.
And the lesson of Section 3? Choose your axes, origins and colour schemes carefully. And take particular care with 3D charts. If you want to be able to read actual data values, a table may be more appropriate than a visual representation.
4 Hierarchical data
Many data sets contain within them – either explicitly or implicitly – a set of structural relations between different parts of the data set.
One common way of structuring data is in the form of a hierarchy, or ‘family tree’. Typical examples are organisational charts and library classification schemes.
There is some optional material on creating organisational data in Microsoft Word and Google Spreadsheets in section 9.2.
Hierarchical diagrams are also widely used as the basis of mind-mapping tools, where ‘child’ ideas are developed leading off from a central core topic. A mind-mapping tool can provide a very good way of helping you ‘unpack’ or explore an idea.
There is some optional material in mind-mapping tools in section 9.3.
One of the problems with displaying hierarchies is that they can get very large – and hard to display – very quickly.
There are several ways around this problem. For example, an interactive visualisation can ‘collapse’ each branch of the tree, hiding the sub-branches until you want to see them. In this sense, hierarchical organisations can also be thought of as containing sets of ‘boxes within boxes’.
You may already be familiar with this sort of approach from your computer – many file managers offer a hierarchical visualisation of file organisation through ‘nested’ folders which you can open up or collapse as you wish. Figure 11 shows an example of this.
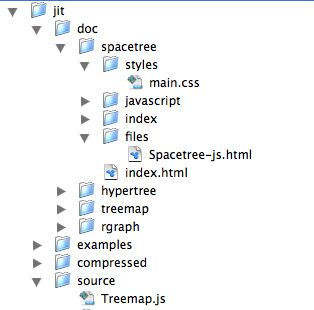
This figure shows a set of folder icons with some of the files having the contents showing as well. At the top left the highest level file is shown. To the left of each folder symbol is an arrowhead and to the right of the folder symbol is the folder’s name. The top folder is called ‘jit’. The arrowhead next to the jit file points downwards indicating that the contents of that file are shown. In the next row down and set 1 jump to the right is another arrowhead with a folder symbol next to it and name next to that. Whenever an arrowhead points downwards the next level of folder or a file is shown underneath. Further down the figure, folders are shown with the arrowhead pointing to the right. In this case no further levels of folder are shown. At levels where there are no further folders, files such as main.css can be seen, with appropriate icons.
4.1 Radial and hyperbolic trees
Sometimes, it is useful to be able to see the ‘full’ hierarchy all in one go. One of the most efficient ways of doing this is to use a radial tree view. A radial tree plots the ‘apex’ of the tree at the centre of a circle, with the ‘child’ branches radiating out from it.
A hyperbolic tree viewer works in much the same way as a radial tree viewer, but uses a different way of visualising the links.
4.2 Treemaps
One colleague still talks about the impact of the first treemap he saw; it was in a blog post by book publisher Tim O’Reilly on the Book Sales as a Technology Trend Indicator (O’Reilly, 2005). It’s shown in Figure 12 below. The reason the treemap made such an impression on him was that one single diagram was capable of portraying several different sorts of information at the same time:
- the relative market share of different topic areas (systems and programming, business applications, and so on);
- the relative market share of different subtopics within each topic;
- the relative growth or decline in market share over the previous 12 months.
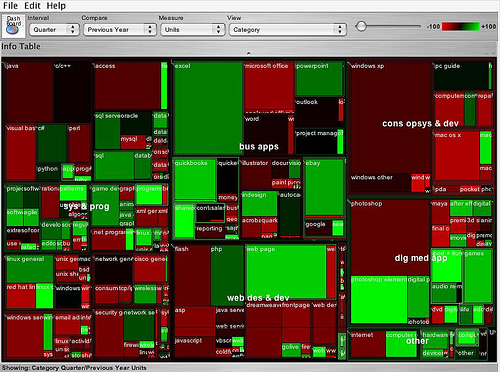
In this screen image a large rectangle is divided into a number of smaller rectangles, each with a label, and within each of those are a number of yet smaller rectangles varying in size. The smallest rectangles are coloured either red or green and in varying shades from bright to dark such that the whole available space is covered in a patchwork of red and green rectangles. Each rectangle has a label; some examples are: ‘Windows XP’, ‘Google’, ‘Microsoft Office’ and ‘Photoshop’. At the top of the window are various drop-down menus. Reading from left to right: Interval (currently showing Quarter); Compare (currently showing Previous year); Measure (currently showing Units); View (currently showing Category).
In addition, the controls at the top of the treemap suggested it was an interactive tool that could potentially be used to explore the data in different ways (the drop-down selection list boxes) or maybe even filter out different results (the −100 to +100 slider). In short, the graphic was powerful and unambiguous, and communicated a lot of different information in one image. The suggestion was also there that the tool that generated it provided a powerful and intuitive way of exploring hierarchically structured data in a dynamic way.
So let’s see how the treemap shown in Figure 12 depicts, at a glance, several different sorts of information at the same time. First, the relative size of the market for different categories of computer books (O’Reilly is one of the best known computer book publishers): the area of each rectangle reflects the relative sales volume of books in one category compared to the others. Second, the year on year change in the volume of sales per category: the chart shows this by using the dimension of colour, with red being market decline and green being market growth.
Activity 8 (exploratory)
Do a web or blog search for “state of the computer book market” to find the most recent O’Reilly review of the computer books market. Visit the review page, but before reading the commentary, just look at the treemap(s) that are presented, and write your own conclusions regarding what they say about the state of the market. Then read through the commentary and compare the conclusions to your own. How ‘intuitive’ did you find the treemap to read?
Comment
Depending on your prior experience and how you respond to visual data, you may find treemaps intuitive to use – or you may even find them confusing.
Have you spotted that the data shown on treemaps can be hierarchical, though only to two levels? For example, Figure 12 has major categories of books sold, indicated by rather cryptic abbreviations such as ‘sys & prog’, ‘web des & dev’, at the upper level. These refer to the ‘window panes’ of the treemap – the areas lying between the thick black lines. At the lower level in Figure 12 are the categories within these major categories. For example, within ‘sys & prog’ are ‘java’, ‘c/c++’ and so on.
Treemaps are a good way of exploring various types of hierarchically organised data. For example, Figure 13 shows a screenshot from the IBM Many Eyes visualisation service, where a treemap has been used to represent the range of course units offered by OpenLearn during its first nine months of operation. Subject Area describes the topic area the course is released under; Original Course describes the course code for the course that the OpenLearn material was taken from; Course Code is the course course identifier for each course on OpenLearn. By rearranging the order of the headers, the treemap can be used to create different hierarchical views of the data, views which might be used to explore the data, or even potentially provide an interactive navigation menu for the materials.

This screen image has the heading ‘Visualizations: OpenLearn Course Units Treemap (DEMO)’. Here a large rectangle is once again divided into several smaller ones which are then sub-divided again into many smaller rectangles. Each of the medium rectangles is a different colour (pale shades of turquoise, blue, peach, yellow, purple, green) and labelled with a different subject area (science and nature, society, mathematics and statistics, arts and history, education and lastly IT and computing). Along the top of the window is a set of headers with the explanation ‘Treemap Hierarchy (Drag to Reorder)’. From the left the headers are ‘Subject Area’, ‘Original Course’, ‘course Code’, ‘Description’, ‘Course Title’, ‘Tags’.
You can find treemaps elsewhere on the web, either as working interactive treemaps, or as simple images (for example, search for treemap (all one word) using your favourite image search engine). One of the most compelling treemaps I have found is the Hive Group World Population treemap, which uses data from the CIA’s online World Factbook to provide a highly interactive way of exploring world population data. If you are interested and have time, you may like to spend a few minutes looking at the Hive Group World Population Statistics treemap.
Activity 9 (exploratory)
Either:
Go back to the Many Eyes site, find the Many Eyes description page about treemaps and read through it. Using this data set based on the medals from the 2008 Summer Olympics, see if you can create your own treemaps to display:
- the distribution of medals by country, ordered by medal type and discipline;
- the distribution of medals by discipline, ordered by country and discipline;
- the distribution of medals by discipline, ordered by country and medal type.
Hint: click on the big ‘visualize’ button to load the visualisation selection page; then click on the big icon that depicts a Treemap to create the treemap visualisation. You should now have a Treemap visualisation.
Note that there may be some issues with running the Many Eyes treemap in certain browsers, including the possibility that your browser will hang. If this happens, force your browser to close using Ctrl+Alt+Del in Microsoft Windows or ‘Force Quit’ in Mac OS X.
Or:
You may prefer to create a treemap from a data set you have uploaded to Many Eyes yourself, either using a data set of your own, one you have discovered on Many Eyes, or one you have located elsewhere. (Take care uploading data to Many Eyes – if uploaded there, it will be made public.)
Read the guidance notes at Many Eyes: treemaps to see how to upload the data in an appropriate format.
As well as the ‘simple’ treemap, Many Eyes can also be used to identify changes in data values in a way reminiscent of the treemaps used in the O’Reilly ‘State of the Book Market’ reports, using the ‘Treemap for comparisons’ (sometimes referred to as a ‘change treemap’) visualisation. If you have a data set you think would benefit from visualisation using one of these types of treemap, the guidance notes on Many Eyes explain how to prepare the data.
Activity 10 (self-assessment)
- a.In what situations might you choose to use a hyperbolic tree visualisation?
- b.How might you use a treemap to display changes in a set of data over time?
Comment
- a.The hyperbolic tree is ideal for dealing with large hierarchical data sets because it allows for the dynamic resizing of parts of the tree that are not currently in focus. So, for example, if you had a very large tree plotted out in a traditional, 2D rectilinear tree view, you would either have to zoom in to areas of the tree you were interested in to look at them, or scroll to the part of the tree you were interested in. The hyperbolic tree makes far more efficient use of space, and allows you to navigate the whole tree, even a large one, in quite a small viewing area.
- b.Treemaps can be used to be display changes in data values between two points in time using the dimension of colour. Typically, the most recent data set will be used to determine the area of each block, and the colour then indicates the degree of change from the earlier data set. So for example, in the O’Reilly book sales treemap, the area of each block represented the current year’s sales, and the colour was the percentage growth (green) or decline (red) in volumes from the previous year, with the intensity of the colour indicating how large or small the change was.
5 Geographical data
Geographical data is, loosely speaking, data that relates to geographical co-ordinates and so can be plotted on a map. The wide range of online mapping tools now available means that it is possible to create a wide range of map-based representations from appropriate data sets very easily indeed. In this section, we will look at how to get data on to a map and then explore three different ways of visualising data on a map: proportional symbol maps, the rather exotic-sounding choropleth maps, and heat maps. We’ll also look at how the transformation of a map projection itself can be used to represent data in the form of a special sort of map known as a cartogram.
But first some orientation.
5.1 Maps on the web
At the start of 2005, Google launched an online mapping service originally known as Google Local, now known more widely as Google Maps. Within a matter of weeks, third-party developers began to work out how to access Google Maps programmatically and create ‘map mashups’ that overlaid third-party data on top of the actual maps. Over the next few months, Google opened up an API – an application programming interface – that made it easier for developers to create their own annotated maps.
Looking around the web today, there is a wealth of online mapping services, some of which are ‘free’, some of which can only be accessed on a commercial basis.
Activity 11 (exploratory)
If the idea of online maps is new to you, spend five to ten minutes familiarising yourself with the capabilities of some freely available online maps, such as the level of detail they offer and how to navigate within them.
For example, visit at least one of the following and see how many different ways you can locate your own home.
A 3D map such as:
Note that your browser may need to install a plug-in if you try to use these 3D maps.
Many mapping services are also available via mobile device web browsers. If you have a mobile device, you may find that it has a mapping application built in that is aware of your location, using phone mast triangulation, Wi-Fi IP address geolocation or an in-built GPS service.
5.2 Making your mark – plotting data points on a map
One of the easiest ways to plot location data onto a map is to add it as an overlay. That is, as a visualisation layer that sits on top of the actual map image layer.
Many web services allow you to place one or more markers on a map and save them so that they can be viewed on a map on the same website – or another website – at a later date. There’s an example of this in Figure 14.

In this screen image a partial map of the world is shown with various markers on it. The top of the image shows the website name ‘Digital Planet’. Underneath to the left are some links to various related sites for example ‘Taking IT further’ and ‘Science & Technology forum’. In the centre, above the map, is the heading ‘Show us your Digital Planet’ with the text ‘We want to see your Digital Planet – use our map to show where and how you listen to the programme’. The map itself has tools to move the map to show other parts of the world and enlarge or reduce the map size. Two types of marker are shown; an orange pin-shaped marker and a green arrow. Neither is explained in this image. Under the map is the text ‘Put yourself on the map’.
Map data can be syndicated, that is, pulled in to a remote map, using a data exchange format that can encode geographical location information, such as the latitude and longitude of a point, and maybe its altitude above sea level.
Two standards that have come to the fore on the geographical web are geoRSS and KML.
geoRSS is a lightweight, emergent standard that extends the RSS syndication protocol with latitude and longitude co-ordinates. Many online mapping tools accept geoRSS, which means that web publishers who publish their content via RSS feeds already can also push that content into a map-based display, if appropriate.
A good example of a site that supports this approach is flickr, the online photo sharing site, which allows users to add location metadata to their photographs, describing the location where they were taken. This information can then be exposed via geoRSS, or the flickr API, and used to create displays such as flickrvision, which plots recently uploaded photos on a map.
As with many online services, flickr publishes RSS feeds as geoRSS if there is location data available for any of the photos listed in the RSS feed.
A second, far more powerful, mark-up language is KML, once known as the ‘Keyhole Markup Language’. This language was originally created for use with the Keyhole 3D geographical visualisation tool that has become Google Earth. KML is now an Open Geospatial Consortium standard.
As well as describing straightforward location information, KML is capable of representing lines and complex polygons (that is, complex 2D and 3D shape overlays), as well as adding image overlays and carrying payloads (such as HTML and embedded video players) into geo-visualisation tools. KML files are often published in a compressed form as KMZ files, which is why you’ll often see Google Earth overlay files linked to files with the extension .kmz rather than .kml. Most services that are capable of accepting a KML file (that is, that will plot the points and overlays described within a KML file) can also read KMZ files.
As an example, click the following link to load a KML/KMZ file of OU Regional Centres into Google Maps.
There is some optional material on exploring KML further in section 9.4, and some optional material on map overlaying skills in section 9.5.
5.3 Geocoding your data
Geocoding refers to the way in which the actual location of a data point (in terms of latitude and longitude co-ordinates, map grid references, or some other reference scheme that allows the data point to be plotted on a map) is obtained from the name of the location, its address, or its postcode. In turn, reverse geocoding refers to the process of taking a map location or co-ordinate and identifying the corresponding address, postcode or ‘toponym’ (that is, the place name).
There is a wide variety of geocoding web services available that can accept either a single address or a set of addresses and return an appropriately geocoded result.
Online map-based search tools all perform some sort of geocoding of addresses or postcodes in order to display locations on the map. For example, you could try typing an address you know into the search box on Google Maps or Yahoo! Maps – does it locate the address properly?
Although it is quite easy to find geocoding APIs for addresses in the USA, thus allowing the creation of applications that can automatically geocode everyday addresses, in the UK the Ordnance Survey and the Post Office have traditionally published UK geolocation data under commercial terms. However, with the move to open up public data it is now possible to access a range of geolocation services in the UK as Linked Data.
Web developers typically access geocoding APIs in order to geocode locations in a programmatic way. The Yahoo! Placemaker™ API provides a location-extracting and geocoding web service that can be accessed via a URL. Pass in an address, or a block of text containing a placename, and it will identify the address and return latitude and longitude data for it. Many social networks make use of geocoding services to allow users to search for people near a particular location.
5.4 Proportional symbol maps
Proportional symbol maps, or more often proportional circle maps, associate a particular symbol, typically a circle, with a particular point on a map, such as the centre of a city, or the capital city of a country. The diameter of the circle represents some function of the quantity being visualised.
For example, the proportional symbol map in Figure 15 depicts the number of internet users per country in 2007 (data source CIA World Factbook; map produced using Many Eyes).
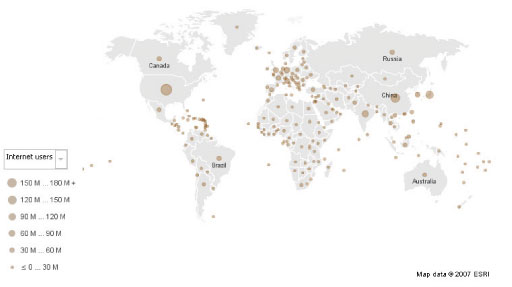
Here a screen image of a world map is shown with brown dots of various sizes scattered over the map. The dot with the largest radius is on the USA and the next largest on China. There are some medium-sized dots on India, Japan and some European countries with slightly smaller dots on the rest of the world. At the bottom left a key explains that dots represents millions of internet users per country. The largest dot represents 150 to 180 million users and the smallest 0 to 30 million.
5.5 Choropleth maps
Choropleth maps are some of the most widely used maps for depicting country- or region-based numerical data on a map. Rather than using markers or proportional symbols to render information about a dataset in a visual way, choropleth maps use shading or different colours (often along a spectrum) to colour well defined geopolitical areas of a map, such as a country, state or county, according to a given dataset.
For example, the choropleth map in Figure 16 visualises the same internet usage data that was used to illustrate the proportional symbol map (data source CIA World Factbook; map produced using Many Eyes).
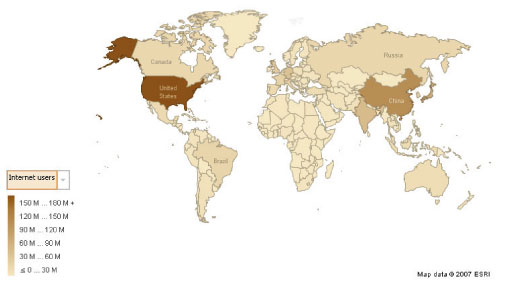
This screen image shows the same world map as Figure 15. Now however each country is shaded in various shades of brown. The darker the shade the higher the number of internet users. The key at the left-hand side shows the shades of brown for the same groups of million users as before. As detailed before, USA has the darkest shading and China the next with India, Japan and some European countries clearly darker than, say, African countries.
Activity 12 (exploratory)
Read through the notes on creating World Map based visualisations on Many Eyes.
Using this dataset (which is slightly more recent than the one used to produce Figures 15 and 16), a dataset that you have found, or a dataset that you have uploaded, use Many Eyes to create both a proportional symbol map view and a choropleth map view of the data.
Note that if you use the foregoing dataset you will have to resolve some incompatibilities between the country names in the dataset and those that the Many Eyes mapping tool expects. Mostly the suggestions of the dialogue box are correct, but you will have to tell it, for example, that Burma is the same as Myanmar.
- a.How do the map views compare in terms of impact and ability to understand the story being told by the data compared to its numerical, tabular representation?
- b.How effectively does the choropleth map communicate the relative extent of internet usage across the world compared to the proportional symbol map?
- c.What drawback do you think there could be to using proportional symbol maps?
Comment
- a.Both maps make it easy to see how the data values vary by country. You probably found that both of them had more impact and gave you a better understanding of the story being told by the data than did the tabular representation.
- b.To some extent the answer to this is personal. For example, if you are used to using maps where countries are coloured to distinguish them then you may find the choropleth map easier to relate to. On the other hand, you may feel that too much significance is given to large countries (whose colours tend to stand out more than do those of small countries) in the choropleth map and so prefer the proportional symbol map.
- c.The principal problem with a proportional symbol map occurs when the symbol size is large compared to the country size. If proportional symbols were used on a higher scale map, for example to display statistics about different postcode areas in a town or city, it might be quite hard to identify which particular area each symbol corresponded to, particularly if some of the symbols overlapped.
Activity 13 (exploratory)
Now read Perceptual Scaling of Map Symbols, a blog post by John Krygier.
How does our perception of area compare with the way we perceive length? What lessons do we need to bear in mind from a psychophysical point of view when choosing between the use of a choropleth map and a proportional symbol map?
Comment
As with many other visualisation techniques, the way we perceive choropleth and proportional symbol maps can be influenced by perceptual psychological and other psychophysical factors.
5.6 Heat (isopleth) maps
Commonly known as heat maps, density maps or isopleth maps use semi-transparent overlays above a map or other image (such as a web page) to show the density (or frequency) of events happening at each point on the underlying map.
In contrast to a choropleth map, where values are plotted for different predefined regions, heat maps show colour-based contour lines that connect points of equal value.
For example, Figure 17, a house price heat map from mousePrice, shows house price inflation in the north-west of England between May 2007 and May 2008.
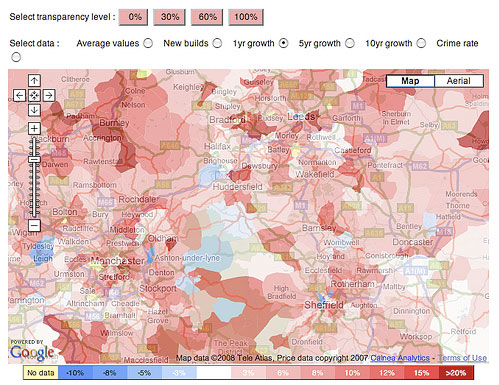
This very busy screen image shows a patchwork of red, pink and blue areas of varying shades overlaying a map of part of the north of England. At the top there are 4 buttons and the text ‘Select transparency level’ with a button for 0%, 30%, 60% and 100%. Under that are radio buttons with the text ‘Select data’ with a button each for the following choices:
- Average values
- New builds
- 1 yr growth
- 5 yr growth (selected)
- 10 yr growth
- Crime rate
On the map town names can be faintly seen. At the bottom a key shows the percentage house price growth relating to each colour. From the left, yellow indicates no data, dark blue minus 10% through various shades of blue to pale pink for 3% up to dark red for greater than 20%.
The ‘hot’ colours (reddish) are naturally taken to mean areas where there was a high one-year growth in house prices and the ‘cooler’ (bluish) colours to mean a lower increase in house prices over the same period – or, indeed, a decrease.
Heat maps have come to be widely used for plotting the incidence of crime within city confines, particularly in the larger US cities. An initiative in 2008 required UK police forces to start publishing crime maps reporting on the level of criminal incidents within their own jurisdiction.
Activity 14 (exploratory)
See if you can find the ‘crime map’ published by your local police authority. (If you don’t live in the UK and don’t have an equivalent where you live, you could try some UK city you may have visited.)
Does your local police authority use a heat map to display the results? If not, see if you can find a crime map that does use heat maps (but don’t spend more than ten minutes on this activity).
If possible, compare the crime heat map to a house price heat map for a similar area; from just the heat maps, does there appear to be any correlation between levels of crime and house price?
Heat maps and density mapping techniques are also widely used for displaying radio propagation data and satellite coverage data. For example, the SatBeams website uses density mapping to plot geographical areas that are covered by particular communications satellites.
Heat maps elsewhere
As well as being used as overlays on geographical maps, heat maps are also widely used to provide reports about website usage. Information can be collected at a crude level based on the links that users click through on a web page to produce a click-density map, although it is possible to also track mouse cursor movements, or, in a laboratory setting, collect eye-tracking data.
Figure 18 shows the result of eye-tracking and mouse-clicking data collected and aggregated from multiple users of the Google website (Enquiro Search Solutions, Inc., 2005). The hot spots (red, orange and yellow colours) are the places on the page that the users were looking at most, and the purple crosses show where users clicked on the page.
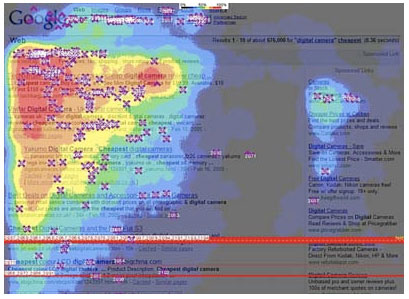
In this screen image a Google search result is shown although the actual results cannot be distinguished. The page is coloured from bright red through yellow to blue with a number of pink crosses showing. The main dark red area is a triangle at the top left hand corner. A larger pale orange triangular border fans out across the page with an even larger yellow triangular border next. Blue areas cover the remainder of the text on the left-hand side. The centre of the page where there is no text is black and then there is a further blue area to the right over the sponsored links list. The sponsored links at the top of the list on the left of the screen fall into the yellow or even orange area.
As well as supporting an understanding of user navigation behaviour on websites, eye-tracking heat maps can also be used to understand better how people read from the screen.
Activity 15 (exploratory)
Read F-Shaped Pattern For Reading Web Content, an article by Jakob Nielsen.
What do the eye-tracking results suggest about how people read web pages? How does the visualisation used in the Google ‘golden triangle’ screen make this sort of generalised pattern of behaviour apparent?
Activity 16 (exploratory)
Suggest two drawbacks of each of:
- choropleth maps
- heat or isopleth maps.
Comment
a.
- The fixed area boundaries in a choropleth maps suggest a discontinuity in the values portrayed either side of an area boundary, and different values of a measure within a geographical area are not shown.
- The use of a limited colour palette means that choropleth maps are unable to depict a wide range of actual values.
b.
- Heat or isopleth maps require a large number of data points in order to identify equal-value lines of a particular measure.
- Heat maps cannot be used in cases where the data is largely discrete or discontinuous – for example, the course codes of Open University courses being studied in households in a particular OU region.
There is some optional material on web developer skills in section 9.6.
5.7 Cartograms
Cartograms are map projections in which the sizes of the countries depicted are dependent on the value of some statistical measure associated with that country. (To a certain extent, treemaps use a similar approach in that the area allocated to a category is proportional to the relative value of a quantity associated with that measure.)
Figure 19 shows a cartogram of the world in which ‘territory size shows the proportion of all telephone mainlines that were found there in 2002’ (Worldmapper, 2006). (Here ‘telephone mainlines’ refers the UN measure of telephone lines connecting a customer’s equipment to the public switched telephone network.)
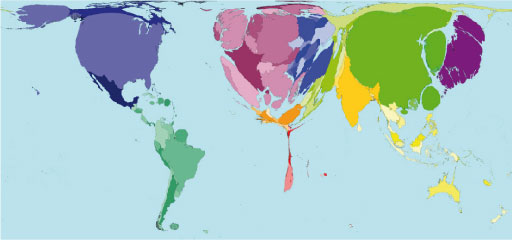
Here a map of the world is shown in various bright colours with the different countries identified by the different colours. However the shapes of the countries are distorted. Whilst the shapes of North and South America are easily recognisable, Europe has become a group of large pink and red blobs. Africa has become relatively tiny and very thin and Japan has also grown hugely.
Note that quantities in international comparative data may often be ‘normalised’. This means that they are not absolute values but are related to the population size itself. So for example, a cartogram might display the number of mobile phones per 1000 people, rather than number of mobile phones in the country as a whole.
Activity 17 (exploratory)
The Show/ World mapper is an online animated cartogram generator that will transform a ‘traditional’ map to an ‘exploded cartogram’ depicting one of several different data sets hosted on the Show/World site:
Worldmapper hosts a collection of several hundred different cartograms, some of which are reprinted in The Atlas of the Real World: Mapping the Way We Live:
Spend a few minutes exploring the cartograms on each site (about five minutes for each site). How easy are the cartograms to understand? What drawbacks are there in using a transformation of country size and shape to communicate statistical measures about different countries, compared to using visualisation techniques such as choropleth and proportional symbols maps within the context of a traditional map projection?
Comment
One major drawback of cartograms is that by distorting the shape of a country, it can become unrecognisable, except in relative terms (for example, I recognise country A, so that mangled shape next to it must be country B). In a choropleth or proportional symbol map, the map colouring or marker placement is typically applied to a map projection we are familiar with
Activity 18 (self-assessment)
You have met several types of map-based visualisation in Section 5. This activity enables you to test your grasp of their relative uses.
What sort of map-based visualisation might you use to display the following sorts of geographical data set?
- a.The approximate travel time to a college campus for students who live within a travel distance of 20 km.
- b.The number of students in each of the universities in England.
- c.The average income in each district of a local city.
- d.Members of your social network who are online at the same time as you.
Comment
- a.Heat maps are a good way of depicting travel time. For example, commuting time maps.
- b.If we assume a single location for each university, a proportional symbol map could be used to display the relative numbers of students at the different universities on a map.
- c.A choropleth map using electoral ward or postcode boundaries could be used to display average income in different areas of a town or city if the data is available for those geographical areas. At a push, you might even get away with using a cartogram to display this information!
- d.A simple marker-based map could be used to display the location of your family and friends on a map.
6 Multi-dimensional data
Multi-dimensional data is data that spans several different dimensions, and potentially many different units of measurement (for example, national statistics for a country might cover birth rate, mortality rate, population size, mean income per capita, average carbon footprint per person, total GDP, total amount of electricity generated per capita, number of mobile phones per capita, and so on).
Being able to visualise several different dimensions of the same data set at the same time can often reveal startling insights about how the data may be correlated. You saw this in the presentation by Hans Rosling that you watched at the start of this course. In this video Rosling is demonstrating the ‘Trendalyzer’ visualisation, which has since come to be called a ‘Motion Chart’.
Whoever thought a statistics talk could double up as a live performance? But did you notice what sorts of techniques Hans Rosling used to explain the story that the animated data was telling?
Activity 19 (exploratory)
Read Six Simple Techniques for Presenting Data: Hans Rosling (TED, 2006).
This analyses Rosling’s presentation, and in particular how he works with the visualisation to narrate the stories the data tells. Then watch the video again.
If you are reading this course as an ebook, you can access this video here: The Best Stats You've Ever Seen | Hans Rosling | TED Talks
Comment
Even if you never have to give a ‘live’ presentation about data, you may still be able to invoke some of the techniques if you ever have to provide a written explanation about a data set.
The Trendalyzer software (also known as a motion chart) that is used to create the Gapminder presentation works best with multidimensional sets of continuous numerical data collected over a long period of time (that is, longitudinal data sets). Such data is often found in the social sciences, as Rosling’s talk suggests.
Activity 20 (exploratory)
There is a great deal of interesting data and many ways of visualising on offer at the Trendalyzer site, so you should aim to spend as much as twenty to thirty minutes on this activity.
Visit the Trendalyzer visualisation tool that Rosling demonstrated, and the UN data he visualised with it at Gapminder World.
You might notice that the application actually provides different ‘views’ over the data - either as a chart against (user selected) numerical axes, or overlaid on a map. Using the Trendalyzer, see if you can spot any trends that relate some or all of internet usage, broadband subscription, mobile phone (called cell phone in the application) ownership and personal computer ownership. (Hint: you can change what’s plotted on the two axes by clicking on the little arrow alongside the axis label and then choosing from the list that will appear.)
Also use the Trendalyzer to look for relationships between these technological indicators and particular economic, trade, education or energy indicators.
If you find any surprising or particularly interesting relationships using the Trendalyzer, save the URL of the visualisation and share it in the Comments section below, along with a brief explanation of what the visualisation depicts and what you found to be particularly notable about it.
Activity 21 (exploratory)
How many dimensions can the Trendalyzer visualise simultaneously, and how can these dimensions be depicted?
How does the Trendalyzer animation help you spot correlations – or anomalies – in the data presented?
Comment
The Trendalyzer allows you to track data along five dimensions: the horizontal axis, the vertical axis, the size of each point (that is, the ‘bubble’ size), the colour of each bubble, and time (when you use the ‘play’ function). You might also view the feature that allows you to identify what each individual bubble represents as giving you access to yet another dimension.
There are many ways in which the Trendalyzer allows you to spot correlations or anomalies. For example, if all European countries are depicted by the same colour of bubble then looking at how the bubbles of that colour move over time will enable you to spot which countries are changing in the same way and which are changing in a different way.
There is some optional material on further visualisation skills in section 9.7.
7 Some caveats
Here are a few final points about using visualisation tools.
First, as more and more use is made of interactive chart components, it is worth bearing in mind that something that is informative as an interactive component may not be so useful if it is printed out. Just as you should always write for an audience, so you should always write for your medium, When designing a data display you should be mindful of what you want it to communicate and the situations in which you want it to be meaningful. For example, the interactive UK stock price charts on Yahoo! Finance allow users to zoom in to different areas of the chart and explore them interactively. If it’s likely that an online document containing an interactive chart will be printed out, you may need to take care in configuring the chart (or the print template for the document) so that an appropriate view of the chart is displayed in the print version. Due consideration also needs to be paid to managing the expectations of the users. For example, if they use the interactive chart to display a particular view over the data and then print the document out, will the view they have selected be the one that gets printed out?
Second, one of the potential problems with using data from public data-sharing websites is that you can’t necessarily guarantee the accuracy, or authenticity, of any particular data set. To be sure of the provenance of the data, you need to either download from a trusted site for original data (such as the UK National Statistics website, the UK Government Data Repository, the World Bank, and so on) or go to a trusted third-party site that in some way guarantees the quality of the data. This is where sites like the Guardian Data store come in. Sites like these maintain directories of ‘qualified’ or otherwise trusted data, as well as curating data themselves. They may even support closely integrated visualisation tools.
And finally, but very importantly, if you do download the data yourself from a website, with the intention of re-using it, then there may be licensing issues that restrict what you can legally do with the data. Further, if you use data from a third-party source, you should always reference it in the same way that you would reference a book or journal article that you may have quoted.
8 Conclusion
One of the aims of this course has been to open your eyes to some (though by no means all) of the visualisation tools and techniques that are available today for visualising data sets, from numerical data to geographical data. Along the way, you have also seen how many institutions and organisations, as well as individuals, are making their own data available so that other people can visualise it to suit their own needs.
9 Taking it further (optional material)
All of the material in this section is optional. If you choose to study any of it, you should be aware that time taken studying this section is not included in the study time for the course as a whole.
9.1 Exploring time-series data (optional)
This page expands on issues discussed in section 3.1.
If you would like to explore other Google search trends, you can find the tool here:
Other sets of time-series data can be found at:
- Time Series Data Library A collection of time-series data drawn from many different subject areas.
- UK National Statistics online This is the UK’s repository for National Statistics, where you can find all manner of UK-related data if you search hard enough!
- Timetric A site you may already have used, in Activity 6, for displaying and analysing time-series data charts.
Several of these sites also provide closely integrated charting tools that let you explore the data in a visual way.
Activity 22 (exploratory)
Choose one or more of the above websites and spend up to 15 minutes exploring what it offers.
9.2 Creating organisational charts (optional)
This page expands on issues discussed in section 4.
If you use Google Spreadsheets, you could look at Google’s alternative way of creating organisational charts:
9.3 Mind-mapping tools (optional)
This page expands on issues discussed in section 4.
If you have never seen – or used – a mind-mapping tool, you may like to try one out. It can be helpful for note taking, mapping out your understanding of a topic, or planning out the structure of a document or presentation.
Search for the terms ‘mind mapping application’ or ‘mind mapping software’ with your favourite search engine to find a tool, and then familiarise yourself with the sorts of diagram these tools can produce.
To get you started, two tools I particularly like are:
- the Freemind desktop application
- and the online Mindmeister.
Using whichever tool you prefer, see if you can create a simple mind map of the topics covered in Sections 1, 2 and 3 of this course.
Related to mind mapping is concept mapping. The Open University’s KMi research department has led the development of Compendium, which is one such concept-mapping tool.
9.4 Exploring KML further (optional)
This page expands on issues discussed in section 5.2.
If you are interested in exploring KML further, you can use the KML Interactive Sampler to see how KML files are structured, as well as how they are then rendered in Google Earth:
Please note that your browser may need to install a plug-in in order to use this application.
A wide collection of KML files can also be found on the Google Earth Outreach site:
See if you can find a KML file that contains a list of UK TV and radio transmitters, and then visualise it using an online map.
9.5 Map overlaying skills (optional)
This page expands on issues discussed in section 5.2.
In order to plot your own geoRSS or KML feeds in Google Maps, use the same construction as I used for the OU data at the end of Section 5.2. That is, start with Google Maps and then add the URL of your geoRSS data. Alternatively, you can simply paste the geoRSS URL into the search box on Google maps and click on ‘Search’.
A similar approach is used by many of the other online mapping services.
New mapping tools that make it easier to display data on maps are being developed all the time. Some examples are:
- OpenHeatMap – plot spreadsheet data easily on a map
- GeoCommons – upload data and create interactive maps
- UK Ordnance Survey OpenData.
If you would rather work on maps at the programming level via map service APIs, Mapstraction provides a Javascript abstraction layer over several popular mapping APIs.
9.6 Web developer skills (optional)
This page expands on issues discussed in section 5.6.
If you would like to create a click density map for a website you control, there are several services you can try for free. For example: ClickHeat, CrazyEgg and clickdensity. How do you think that heat maps might be used to help in improving the usability of a website?
In order to add rich visualisations and charts to your website, there are several frameworks and libraries available. Some examples are:
- Google Chart Tools/ Image Charts – create charts by passing data to an image server via a URL, and let it return the image file directly
- Protovis – Javascript and SVG visualisation library
- gRaphaël – Javascript chart library
- jqPlot – one of several JQuery plugins providing support for charts
- Mapstraction – a Javascript abstraction layer over several popular mapping APIs
- theJIT – Javascript libraries with a particular emphasis on rendering hierarchical/tree-based data structures.
9.7 Further visualisation skills (optional)
This page expands on issues discussed in section 6.
If you ever want to create Trendalyzer-style visualisations using your own data, use a Google ‘Motion Chart’ gadget, either from within a Google spreadsheet, or via the Google Visualisation API.
The Trendalyzer/Google motion chart widget is also used as one of the visualisation tools provided as part of the Google Web analytics service. If you are interested in how the motion chart can be used in such a context, you can watch a demonstration video called Motion Charts in Google Analytics (it lasts just under three minutes):
Motion Charts in Google Analytics
With ever-increasing amounts of data being published, data-handling and visualisation skills, as well as knowledge of statistics, are becoming more and more important. To keep up with innovations in visualisations, the following blogs are well worth subscribing to:
References
Acknowledgements
Grateful acknowledgement is made to the following source for permission to reproduce material in this course:
Course image: Walter in Flickr made available under Creative Commons Attribution 2.0 Licence.
Figure 12: Taken from http://radar.oreilly.com/.
Don't miss out:
If reading this text has inspired you to learn more, you may be interested in joining the millions of people who discover our free learning resources and qualifications by visiting The Open University - www.open.edu/ openlearn/ free-courses
Copyright © 2016 The Open University