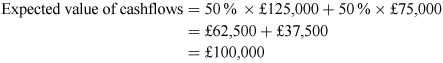4.3.3 Estimating probabilities for scenarios instead of increasing the discount rate
Here is a similar scenario. Say a project requires an £800,000 investment to develop a new product. If the market demand for the product is good, an expected income of £125,000 per year in perpetuity will be generated. However, if demand is poor the income in perpetuity will only be £75,000. The company estimate good demand at only 50% likelihood, so uses a discount rate of 25% rather than their cost of capital of 10% (which is the standard return for selling established products in their industry). Discounted cash flow calculations show that the project is not worthwhile:
So the NPV of the project equals (£400,000), and the project is clearly not worth pursuing.
However, this is using the discount rate to account for the uncertainty in the success of the project, not the uncertainty of the project once it is established. To look at it another way, the company justified using a large discount in the first year because the demand is unknown. However, after the outcome of the first year is known, will the level of additional risk be as high for the second and subsequent years?
The answer is probably no: after the first year, whether the product is successful or unsuccessful, cash flows in the second year and onwards will continue to be high or low, depending on the outcome of the first year. So a further discount of 25% for income in the second year, third year, etc. is not warranted. (Obviously this is a simplification, since cash flows from a new product are unlikely to be constant each year.)
If we could resolve the uncertainty about the success of the product, we could avoid using this fudge factor in the discount rate. The company thinks that if it carried out some market research before investing in the project, it would be able to determine whether demand for the product would be good or poor. This market research would cost £25,000 and take place just before paying out the £800,000 investment.
The two scenarios can now be looked at separately. Since the market research removes the risk of how well the product is received, the discount rate for the normal selling of products in this industry can be used, rather than for launching products.
Poor demand
![]()
So the project is actually worth undertaking if there is good demand, but not if there is poor demand. If the company knew in advance there was poor demand, it would not actually invest in the project, whereas with good demand the project has an NPV of £450,000 and would be invested in.
However, a company may be reluctant to invest in the project while there is risk about the levels of demand, in case there was poor demand and the project generated negative NPV. So it would want to carry out the market research to remove this risk.
In this scenario, the company can find out whether there would be good demand by spending an additional £25,000 on market research, before having to decide whether to go ahead with the £800,000 investment. So, the decision to make now is whether to go ahead with the market research! To do this, we calculate the expected NPVs of the project with and without paying for market research first.
Once the market research is completed, the company will know whether demand will be good or poor, and will invest or not depending on this knowledge. The probability-weighted NPV of the project can be calculated, taking into account that the company will have to pay for the market research to make its decision about investment.
The probability-weighted NPV of the project is found by multiplying the NPV in each case by its estimated probability, and deducting the cost of the market research. The probabilities of good demand and poor demand have already been estimated as 50% for each by the company.
Market research
This is undertaken in both scenarios.
There will be a positive NPV of £200,000 with the benefit of the market research, even after paying for the market research itself, so the project will go ahead. This demonstrates the benefits of trying to determine the probabilities of future outcomes, rather than simply adjusting the discount rate higher to account for increased uncertainty.