Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Environment: understanding atmospheric and ocean flows
Environment: understanding atmospheric and ocean flows

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

3.2 The past temperature of the planet

Measuring the concentration of lead in the ice is called a direct measurement: the ice sample is melted and the water produced contains a very small but readily measured quantity of lead dust. A very accurate set of scales is needed to measure it, but it is a directly measured quantity.

There are also many indirect measurements that can be made using proxies. The concept for using proxies is both simple and brilliant: one measured property allows inference about other states of the system (Box 1).

Box 1 Proxies and correlation

The word proxy is used in various settings to mean a stand-in: representing someone or something else. One example is a proxy vote, where one person agrees to represent the voting intention of another person in the voting booth. In science, the word ‘proxy’ is used when scientists measure one, two or even several direct quantities and use these values to infer some other quantity they wish to know. This is an indirect method of measurement. It is possible for measurements of one quantity to represent another quantity when there is a relationship between the two. You can say that the quantity is a proxy, and that the measurements of the quantity are proxy data.

Take the following as an example:

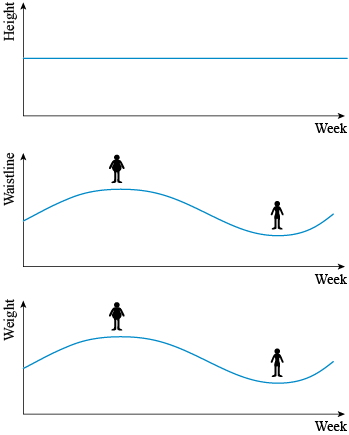
I measure my waistline, my weight and my height every week for a year, there will be a data set consisting of three variables measured 52 times over the course of a year. They are called variables because they are varying quantities; in this case, they vary with time. Typical results might be like those shown in Figure 12.

Because I have stopped growing, my height does not change throughout the year so, as in the top panel of Figure 12, the graph is a flat line. However, both my waistline and weight do vary. With my body shape, when my weight goes up it all goes onto my waistline, so the graph of my waistline and the graph of my weight vary in the same way. As my waistline gets bigger, I get heavier. The opposite also applies – when my weight goes down, my waistline reduces. Because my waistline and weight seem to vary together, you say the two variables are correlated. In this case, they are positively correlated because when my waistline gets bigger, so does my weight. If, for some strange reason, as my waistline got bigger my weight decreased (not a likely scenario!), then the two variables would be said to be negatively correlated.

Described image
Figure 12 Schematic measurements of height, waistline and weight for the author throughout a year
Show description|Hide description

A schematic of three graphs showing characteristics of the author over a year. In the top graph the horizontal axis is time measured in weeks and the vertical axis is height. In the middle graph the horizontal axis is time measured in weeks and the vertical axis is waistline, and in the bottom graph the horizontal axis is time measured in weeks and the vertical axis is weight. There are no units on any axis. The height of the author does not change over the year and so the data on the top graph is a flat line parallel to the horizontal axis, i.e. the value for height does not change. The data on the middle graph (the author’s waistline) and bottom graph (the author’s weight) do vary throughout the year and they vary together. For the first quarter of the timescale both the middle (waistline) and bottom (weight) graphs show similarly increases. For the second and third quarters of the timescale both plots show a decreases. Finally, for the last quarter, both plots show increases again. The three graphs show that although the author’s height does not change over the timescale, the author’s waistline and weight vary proportionally.

Figure 12 Schematic measurements of height, waistline and weight for the author throughout a year

Because my waistline is correlated to my weight, there is a mathematical relationship between the two variables. So, for example, it might be that when my waistline increased by 2 cm, I was 1 kg heavier. If I just gave you the data for my waistline over a year, and my starting weight, you could derive values for my weight over the whole year. This makes my waistline a proxy for my weight. If I then told you that I tended to eat more over Christmas and exercised a lot in the summer, then you could think it reasonable to add dates to the graphs in Figure 12. My weight and waistline would then be a proxy for the time of year as well.

It is important to understand that correlated variables do not tell you anything about the cause of the observation – they only tell you that the items vary in a particular way. In the example above, clearly the expansion of waistline is not the cause of weight changing – it is the result of it. A more extreme example of this is that the number of people in the British armed forces has decreased since the First World War, and at the same time global atmospheric temperatures have risen. While these two variables are negatively correlated, there is no physical mechanism for one influencing or controlling the other.

So, just because two things are correlated it does not necessarily mean that one causes the other, although in the case of the lead data there is an obvious causal link. What is perhaps not so obvious is that you cannot be sure just by looking at a graph whether two variables are correlated.

To be sure that the observations do show correlation, scientists use formal statistical tests. The details of these are beyond the scope of this course, but they are essential in scientific investigation. In principle, statistical tests use mathematics to tell the likelihood that the results you see occur just by chance. If the mathematics suggest that the results are indeed just chance, you cannot draw any conclusions from them. If, however, the likelihood of it being just a chance relationship is very small, then you can assume that there really is some robust relationship between the two.

To use one item as a proxy for others, you therefore need first to be sure that there really is a correlation, according to accepted scientific standards. Observing a correlation should also lead you to look for a plausible mechanism whereby one item affects the other. In the example of temperature and service personnel given above, such a mechanism is almost totally implausible. Even if the correlation were statistically acceptable, its implausibility would lead a scientist to reject it as being due to chance.

Activity 5 Proxy variables

Timing: Allow about 10 minutes

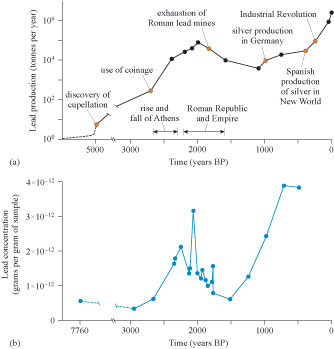
Do the data in Figure 11 suggest that lead production and the concentration of lead in ice cores are correlated, so that one could be used as a proxy for the other?

Described image
Figure 11 (repeated) (a) Global lead production; (b) the concentration of lead in a Greenland ice core (years before present or ‘BP’) (adapted from Hong et al., 1994)
Show description|Hide description

Figure 11(a) shows a graph showing total global lead production. The horizontal axis is time and it ranges from a minimum of 5000 years before present on the left to the present day on the right; the scale is non-linear. The vertical axis is lead production in tonnes per year in a logarithmic scale and ranges from 0 at its minimum to 106 tonnes per year at its maximum. At 5000 years before present the production of lead was first discovered and production is at the minimum. This is labelled as ‘discovery of cupellation’ on the graph. A second point on the graph, around 2700 years before present, is labelled ‘use of coinage’ for which the lean production is between 102 and 103 tonnes per year. This point coincides with the start of the period labelled ‘rise and fall of Athens’ which lasts until about 2300 years before present. There is a peak of lead production around 2000 years before present at around 105 tonnes per year. After this peak, at about 1800 years before present, the graph is labelled ‘exhaustion of Roman lead mines’. Lead production then falls relatively slowly to 1000 years before present at around 104 tonnes per year, before starting to rise again. At about 1000 years before present, the graph is labelled ‘silver production in Germany’. Lead production rises slowly at first until about 300 years before present, when about 6x104 tonnes per year were made. This point is labelled ‘Spanish production of silver in the New World’. After this, the production of lead increases rapidly to more than 106 tonnes per year at present time. Figure 11(b) shows a graph showing the lead concentration in a Greenland ice core. The horizontal axis is time and it ranges from a minimum of 7760 years before present on the left to the present day on the right. The horizontal scale is non-linear although the times from 3000 years BP to present line up with the graph in (a). The vertical axis is lead concentration in grams per gram of ice core sample and ranges from less than 1x10−12 at its minimum to 4x10−12 grams per gram of sample at its maximum. There is a very low lead level of less than 1x10−12 grams per gram of sample up until 3000 years ago. The concentration then rises rapidly to a maximum of more than 3x10−12 grams per gram of sample around 2000 years before present which coincides with the exhaustion of the Roman lead mines. The lead concentration then falls back to very low values about 1800 years before present. The lead concentration then rises to reach a maximum of about 4x10−12 grams per gram of sample about 500 years before present.

Figure 11 (repeated) (a) Global lead production; (b) the concentration of lead in a Greenland ice core (years before present or ‘BP’) ...

Answer

Yes, they do appear to be correlated as the values rise and fall together. There is also a direct physical link between the two items, so it might be acceptable to use one as a proxy for the other.

The example in Activity 5 shows that some measurements can be direct or a proxy, depending on the question of interest. If you wish to know about lead dust concentrations in Greenland ice in the past, you can measure them directly from the lead dust trapped in ice cores. If you wish to know about global lead production in the past, you can try to use measurements of lead concentrations in Greenland ice cores as proxy data, as long as you can estimate the relationship between the two.