1.4.1 Percentages and parts per million (ppm)
This study note will look at how to calculate percentages and percentage change, as well as parts per million (ppm).
Study note: Percentages and parts per million (ppm)
Percentages (%) indicate proportions and show the number of parts out of 100. For example, 30% is 30 out of 100 and 65.2% is 65.2 out of 100.
To find out the percentage of something, first convert the figures into a fraction and then multiply by 100. For example, if 42 people in a group of 70 vote for a political party, the percentage voting for that party is 42 divided by 70 multiplied by 100, or 42/70 × 100 = 60%.
If you already have a fraction and want to change it to a percentage, you multiply by 100. So three-quarters expressed as a percentage is 3/4 × 100 or 300/4 = 75%.
Similarly, to change a decimal to a percentage, you multiply by 100. For example, the decimal number 0.25 expressed as a percentage is 0.25 × 100 = 25%.
To change a percentage to a fraction, or to a decimal, the percentage is divided by 100. So for example, 30% expressed as a fraction is 30/100, or 0.30 as a decimal; and 65.2% is 65.2/100 or 0.652. Thus for example,
Percentage changes
Repeated measurement of an environmental indicator makes it possible to assess change over time. Change between two given dates is often expressed as percentage change in which the figure at the later date is expressed as a percentage of the earlier one.
Calculation of percentage change is best done in stages. For example, if you wish to calculate the percentage increase of atmospheric CO2 levels, which were 360 parts per million (ppm) in 1995 rising to 378 ppm in 2005, then:
- The increase is (378 – 360) ppm = 18 ppm.
- As a fraction of the original value, this is 18 ppm/360 ppm = 1/20 (or 0.05).
- As a percentage change, this becomes 0.05 (or 1/20th) × 100 = 5% increase.
Note that you always divide by the original (earlier) value regardless of it being numerically larger or smaller than the later one. If it is larger than the later value, then this would be a percentage decrease, which is sometimes written using a minus sign before the number e.g. –5%.
You can also use percentage change the other way round. Suppose you plan to reduce carbon emissions of 350 kg by 20%. What would the new value of emissions be?
There are two ways of tackling this question. Either:
- A 20% reduction leaves 80% of 350 kg of emissions to remain.
- 80% of 350 kg is 80/100 × 350 kg = 280 kg as the new reduced value.
Or:
- 20% of 350 kg is 20/100 × 350 = 70 kg.
- Subtract 70 from the original 350 to give the new reduced value of 280 kg.
Parts per million
Parts per million (ppm) is an alternative to percentages that can be useful for very small proportions. As the name implies, ppm represent the number of parts out of a million (1 000 000) instead of 100. For even smaller proportions, parts per billion (ppb) may be used.
Like percentages, ppm can be converted into a fraction or a decimal. For example, an atmospheric CO2 level of 400 ppm can be written as 400/1 000 000. This can also be expressed as a decimal as 0.0004. The following sequence shows this conversion step by step.
At each step, the top and bottom terms of the fraction are both divided by 10 so the overall value of the fraction does not change.
The fraction 400/1 000 000 that you started with has been simplified by dividing the top and bottom terms by the same number. This is called cancelling out. When you are working through a calculation by hand this is shown by crossing through the numbers that cancel each other out, like this:
Conventionally, fractions are written in their simplest form. In this case, you can simplify further because both top and bottom are divisible by 4 so this fraction can also be written as 1/2500. You can also see from the term 0.04/100 in the sequence above that this is equal to 0.04%.
Activity 2 Calculating percentages
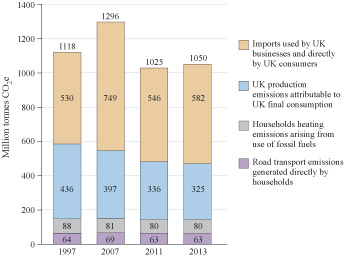
Look at Figure 4 from Section 1.4 repeated again above.
- a.What percentage of the total UK carbon footprint of 1050 million tonnes CO2e in 2013 is represented by household road transport emissions?
Answer
In Figure 4, household road transport emissions are 63 million tonnes (Mt) CO2e. As a percentage this is 63/1050 × 100 = 6%.
- b.What is the percentage change in the total UK carbon footprint between 1997 and 2013?
Answer
The difference in emissions between 1997 and 2013 is a reduction of 1118 – 1050 = 68 Mt CO2e.
As a fraction of the 1997 footprint this is a reduction of 68/1118.
As a percentage, this is a reduction of 68/1118 × 100 = 6.0829 = 6.1% (rounded to one decimal place). You will look in more detail at rounding numbers in Section 2.
- c.If the UK managed to reduce its 1997 carbon footprint of 1118 Mt CO2e by 35% by 2020, what would be the resulting footprint?
Answer
A reduction of 35% means that 100 – 35 = 65% of the 1997 footprint remains in 2020.
65% of 1118 Mt CO2e is 65/100 × 1118 = 726.7 Mt CO2e.