2.3.4 Rounding numbers, decimal places and significant figures
In this study note you will look at decimal places, significant figures and rounding numbers, as well as how to choose what precision to give an answer.
Study note: Rounding numbers, decimal places and significant figures
Rounding numbers
Numbers are often ‘rounded up’ or ‘rounded down’ depending on how precise they need to be. Often a good approximation of a number is adequate, and this process is called ‘rounding’.
When rounding a number up or down you need to look at the digit immediately to the right of the digit you are rounding to. If this right-hand figure is between 0 and 4 (i.e. less than 5), then the digit you are rounding to stays the same, and if it is between 5 and 9 (i.e. 5 or greater), then it is raised to the next whole number. For example:
62 to the nearest 10 is 60, as the digit to the right of the 6 is 2, which is between 0 and 4, so the 6 remains the same;
2932 to the nearest 1000 is 3000, as the digit to the right of the 2 is 9, which is between 5 and 9, so the 2 is rounded up to a 3.
Decimal places and significant figures are two commonly used ways of rounding.
Decimal places
Decimals are often rounded to a given number of decimal places. Decimal places are those to the right of the decimal point, e.g. 5.368 has three decimal places. To round this to two decimal places: find the second decimal place (6) and look at the number to its right (8). As that number is between 5 and 9, the second decimal place is rounded up to the next whole number, which is 7. So 5.368 rounded to two decimal places is 5.37.
To round 5.3634 to two decimal places: the second decimal place is 6 and the figure to its right (3) is less than 5, so the 6 remains as it is. So, 5.3634 rounded to two decimal places is 5.36.
Significant figures
If you are dealing with very large or very small numbers, rounding to a number of decimal places is not convenient. Instead you need a way of rounding numbers that just considers the most important digits in each number. These are called significant figures and tell you roughly how big or how small the number is. The first significant figure in a number is the first non-zero digit on, or starting from, the left (ignoring the location of any decimal point).
For example, the first significant figure in 3 246 485 is the 3. It tells you that the number is between 3 and 4 million. The first significant figure in 0.00245 is 2, which tells you that the number is between 2 and 3 thousandths. You can round a value to any number of significant figures in a similar way to decimal places.
Here are two examples:
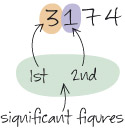
Rounding 3174 to 2 significant figures (the abbreviation ‘sig. fig.’ or ‘s.f.’ is often used).
The first s.f. is 3 and the second is 1. The digit to the right of the 1 is 7; this is between 5 and 9, so the second s.f. is rounded up to 2, giving the answer: 3174 = 3200 (to 2 s.f.).
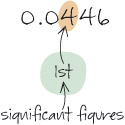
Rounding 0.0446 to 1 s.f.
The first s.f. is 4. The digit to the right is 4; this is between 0 and 4, so the first s.f. remains as 4, giving the answer: 0.0446 = 0.04 (to 1 s.f.).
Choosing appropriate precision
When using data or measurements in a calculation, you may need to decide how much to round off the final result, especially if you use a calculator that shows many digits. The rule is that the final result shouldn’t be more precise than the data used to produce it, and this should be the number of significant figures in the answer.
For instance, in Activity 4 you compared UK mean carbon footprints with those of other countries. For India, the calculation was (6.4/1.7) = 3.764705882 tonnes on a calculator. The original data were given to 2 s.f., so it is appropriate to round the final result to 3.8 tonnes (to 2 s.f.).
If the original data are not all given to the same number of significant figures, then the least precise item limits the final precision. For instance, in Table 2, the ratio for UK/Uganda emissions is 6.4/0.1 = 64 tonnes. The Uganda value of 0.1 is given to only 1 s.f., so the answer should be 60 tonnes (to 1 s.f.).