2.4 Going down: using scientific notation for small numbers
You saw in Section 2.2 how the powers of ten notation provides a concise method of expressing very large numbers and reduces the chances of errors when, otherwise, many zeros would have to be written out. You will now see how the powers of ten notation can be extended to cover small numbers, such as 0.000 000 0002 m.
Write down the next two numbers in each of the following two sequences.
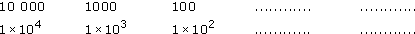
In the first sequence, each successive number is divided by 10 (i.e. one zero is taken off the end) so the number that follows 100 is 
. The next number in that sequence must result from another division by 10. That is, you must divide 10 by 10 and 
. Therefore, the second answer is 1. In the second sequence of numbers, each successive number has 1 subtracted from its power, so the first answer is 1 × 101 because 2 - 1 = 1. For the second answer, you must subtract 1 from the power 1. Because 1 - 1 = 0, the next answer is 1 × 10°.
In fact, both sequences are the same because 10 000 is 1 × 104, 1000 is 1 × 103, 100 is 1 × 102, and 10 is 1 × 101. The implication is that 1 = 1 × 100 and hence 100 = 1. This makes perfectly good sense if you recall that, in the second sequence given above, the power is the number of times that 1 is multiplied by 10 (e.g. 102 = 1 × 10 × 10). For 1 × 100, 1 is multiplied by 10 no times at all, leaving it as 1.
Why stop at 1 or 100? Using the same rules, write down the next number in each of the following sequences.
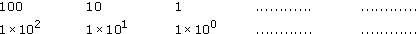
In the first sequence, dividing 1 by 10 gives 
or 0.1 as the next number. Here, decimals are being used, so the answer you want is 0.1. But what about the second sequence? The answer is more straightforward than it may seem. You continue to subtract 1 from the powers of ten so that the next number in the sequence has a negative power of ten (1 × 10−1) because 0 − 1 = −1. Remembering that the two sequences are equivalent, it seems that 1 × 10−1 = 0.1. This is exactly right! You could equally write 10−1 = 0.1.
Just as a positive power often denotes how many times a number is multiplied by 10, so a negative power of ten denotes how many times a number is divided by 10. For 10−1' you must divide 1 by 10 once and you get 0.1.
Question 2
What is the meaning of 10−2?
Answer
The power is now −2, so you must divide 1 by 10 twice. That is, 1 ÷ 10 ÷ 10 = 0.01.
Another way to think about powers of ten for very small numbers involves shifting the decimal point. A negative power of ten denotes the number of places that the decimal point moves to the left. For example, think of 1 × 10−2, which is written as 1.0 × 10−2 to remind you of the position of the decimal point. Starting with the number 1.0, the power of −2 requires the decimal point to be moved two places to the left. One place to the left gives 0.1 and two places 0.01.
You therefore have 10−2 = 0.01.
Try an example. Suppose a raindrop has a breadth of about 0.002 m. This distance could be given in scientific notation as 2 × 10−3 m. This is clear from the following series.
Start with: 2
Divide by ten: 2 ÷ 10 = 0.2 = 2 × 10−1
Divide by ten again: 2 ÷ 10 ÷ 10 = 0.02 = 2 × 10−2
And again: 2 ÷ 10 ÷ 10 ÷ 10 = 0.002 = 2 × 10−3
Alternatively, in considering the meaning of 'two times ten to the power minus three,' you could start with the number 2.0 and move the decimal point three places to the left to give 0.002.
You know from Section 2.2 that when expressing large numbers in scientific notation, the power of ten (which is positive) denotes the number of places that the decimal point moves to the right. Similarly, when expressing small numbers in scientific notation, a negative power of ten denotes the number of places that the decimal point moves to the left.
You have seen that a negative power of ten tells you how many times you need to divide by ten, so that
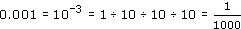
Of course, 1000 = 103, so
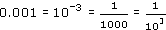
and so
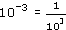
This relationship between positive and negative powers of ten is quite general, so
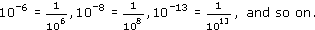
Recall from Section 2.2 that, when writing large numbers in scientific notation, the power of ten should be accompanied by a number that is equal to or greater than 1 but less than 10. The same convention is used when dealing with small numbers and hence negative powers of ten. This is why 0.002 m, the width of the raindrop, is given in scientific notation as 2 × 10−3 m, and not as 0.2 × 10−2 m or 20 × 10−4 m.
To enter a number such as 5 × 10−16 on your calculator, you may need to use the button labelled something like +/− or ± in order to enter the negative power.
Question 6
Express the following measurements in scientific notation.
(a) A water molecule, about 0.000 000 0002 m across;
(b) An average-sized sand grain (on a gently sloping beach), about 0.000 25 m across;
(c) The size of one particle of clay, the main constituent of mud, about 
across
(d) The average size of a hailstone, 0.0035 m across
Answer
(a) The starting point for quoting 0.000 000 0002 in scientific notation is 2.0 (the number between 1.0 and 9.9). The decimal point has to be moved ten places to the left to reach 0.000 000 0002, so the power of ten must be −10 and the answer 2 × 10−10 m.
(b) 2.5 × 10−4 m.
(c) First, convert the fraction into a decimal. This is 0.000 001. In scientific notation, this is 1 × 10−6 m. Alternatively,
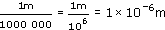
(d) 0.0035 m = 3.5 × 10−3 m.
Question 7
Write out in full the decimal numbers corresponding to:
(a) 7.3 × 10−4
(b) 2.9 × 10−7
Answer
(a) To find the decimal number corresponding to 7.3 × 10−4, the decimal point in 7.3 has to be moved four places to the left to give 0.000 73. The alternative approach is to think of, and work out,
7.3 ÷ 10 ÷ 10 ÷ 10 ÷ 10.
(b) 0.000 000 29
Question 8
To check that you can use your calculator for scientific notation, including negative powers of ten, do the following calculations.
(a) (6.5 × 10−27) × (2.0 × 10−14)
(b) 108 ÷ (2 × 10−17)
Answer
(a) 1.3 × 10−40
(b) 5 × 1024