5.3 Body size and surface area
You will be using some more maths in this section. Remember that areas are measured in units such as m2, which is read as metres squared or, more usually, square metres. Volumes are measured in units such as m3, which you should read as metres cubed or, more usually, cubic metres. Most measurements in science have units attached to them and you should never write down a number without its unit, if it has one. Some numbers don't have units, such as the ratio of one number to another. For example, if you had two jugs, one with a volume of 1500 cm3 and another with a volume of 500 cm3, the ratio of their sizes would simply be 3 (with no units), meaning that the first jug has three times the volume of the second one.
Why should the amount of surface that a mammal presents to its environment be of interest? Because body heat can be either lost to or gained from the external environment via the body surface. The larger the surface area of a mammal, the greater the potential rate of heat loss or gain. Let's concentrate for the moment on problems of heat loss. The fact that body temperature (i.e. Tb, a symbol introduced in S182_1) is so very often greater than outside, or ambient, temperature (Ta) means that frequently the direction of heat 'flow' is from the animal to the outside, i.e. heat is lost from the animal. (Other factors influence the direction of heat flow, such as how much solar heat is absorbed, but I'm ignoring them in order to keep things straightforward.) For a mammal struggling to regulate its body temperature at a relatively constant value, heat lost to the outside, via the surface, must be replaced by heat obtained from the breakdown of food.
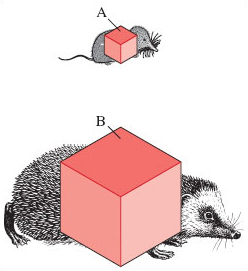
First, let's consider how the surface area of an animal relates to body size. We'll look at two mammals of very different body size; their relative proportions can very approximately be represented as two cubes of different dimensions, as in Figure 7. Follow the arithmetical steps carefully:
The smaller species, the shrew, is represented by cube A with a side of length of 4 mm.
The area of each cube face is 4 mm × 4 mm = 16 mm2.
As there are six faces to the cube, the total surface area is 16 mm2 × 6 = 96 mm2.
The volume of cube A is: 4 mm × 4 mm × 4 mm = 64 mm3.
The ratio of surface area to volume for species A is therefore 96/64 = 1.5. So for the shrew, the value for the surface area is 1.5 times greater than the value for the volume.
The larger-sized hedgehog is represented by cube B in which each side is 25 mm long.
This gives a total surface area of 25 mm × 25 mm × 6 = 3750 mm2.
The volume is of cube B 25 mm × 25 mm × 25 mm = 15 625 mm3.
The ratio of surface area to volume is 3750/15 625 = 0.24.
SAQ 7
What can you tentatively conclude from Figure 7 about the effect of body size on the ratio of surface area to volume and the resultant heat loss?
Answer
The smaller the animal, the larger is the surface area to volume ratio. Therefore, a small animal like a shrew has a greater potential for losing heat from its body because of its relatively large surface area.
In Figure 7, I've been a bit 'free and easy' with my estimates of body dimensions. The figure is a rough approximation - good enough for my purposes. I was tempted to draw in a third cube, representing a very sizeable insect eater such as the giant anteater. But even if I kept to only roughly the right proportions, the animal's outline and the corresponding cube would occupy a full page, so I hope the point is clear enough from Figure 7 as it is.
There's an important inference to be drawn here, which helps explain the relationship in Figure 6. A relatively large surface area (as with the shrew) will lead to a greater heat loss per unit mass of animal. In order to compensate for this enhanced heat loss, a mammal's metabolic rate has to be sufficiently high to maintain its body temperature at a steady value of 36 °C or so. Hence, generally speaking, the more massive an animal, the lower its heat loss relative to its size. In this sense, very large animals have relatively low running costs. Their food requirements are modest - not in the absolute sense of the total amount of food ingested, measured say in kilograms, but relative to their body size, i.e. kilogram of food per kilogram of body mass.
One way of avoiding excessive heat loss is to increase insulation. Rather than constantly eating, why don't small mammals increase insulation? The coat of small mammals simply cannot be thick enough to provide adequate insulation in cold conditions. Thickness of the fur coat is limited by the amount of fur animals can physically carry. If a shrew had an effective winter fur coat, its feet would not reach the ground! For large insect eaters living in temperate climates, e.g. anteaters, effective insulation by fur is more feasible.
