3.3 Enlarging shapes using repeating tiles

The activities in this section can be linked to enlargement as a transformation.

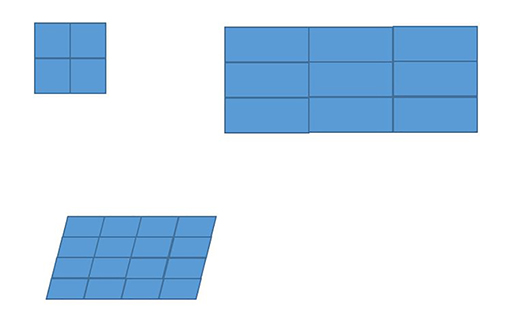
Some shapes can be enlarged when several smaller versions of themselves are laid together (Figure 19). Squares, rectangles and parallelograms all come into this category. Note how many of these shapes fit together to make an enlargement which is two or three or four times as big.

Figure 19 Repeating tiles

Show description|Hide description

Three diagrams which show: A square made from four smaller squares, A rectangle made of three smaller similar rectangles in a three by three array, A parallelogram made of sixteen smaller similar parallelograms in a four by four array.

Figure 19 Repeating tiles

Triangles are also repeating tiles. Try this with different versions of a triangle. You can either make a triangle tile from card or using ICT. You may have to rotate some of the triangle tiles.

Activity 16 Using repeat tiles to make a version which is twice the size of the original

Timing: Allow 10 minutes

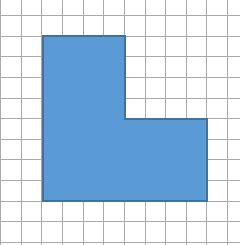
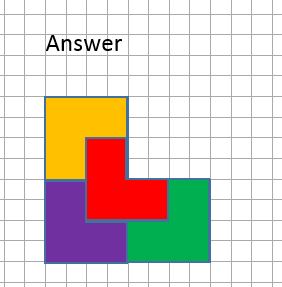
Explore other shapes which can be used as repeating tiles. For example, show how the shape below can be generated from four smaller versions of itself.

Figure 20 An L-shaped tile which can be made from four smaller L-shaped tiles

Show description|Hide description

An L-shape which has a length and height of eight units with the shorter sides all being 4 units long.

Figure 20 An L-shaped tile which can be made from four smaller L-shaped tiles

Discussion

Figure 21 The solution to Activity 16

Show description|Hide description

The L-shape from figure twenty shown split into four smaller similar L-shapes.

Figure 21 The solution to Activity 16

Repeating tiles as an activity with learners

This task gives the opportunity for learners to create and manipulate cardboard tiles in order to explore which shapes are repeat tiles. Alternatively, the tiles could be produced using ICT. For example, some shapes are generated by the ‘Insert Shapes’ facility of Microsoft Word.

Repeat tiles provide an approach to enlarging shapes because the final result of placing together several repeat tiles must be a correct larger version of the original repeat tile. When four repeat tiles are joined together then the length of each side of the enlargement is 2 times the length of the side of the original tile. In order to create a shape where the lengths of each side are 3 times the original tile, you need to use 9 tiles.

Learners can investigate the number of tiles needed to generate enlargements of 2, 3, 4 and 5 times the original tile.

This can lead to the observation that the factor of enlargement for area is the square of the factor of enlargement for lengths.