5.3 Calculating theoretical probability
As well as conducting your own probability experiments, you can calculate the theoretical probability of events occurring using what you know about the event and the other possible outcomes.
In order to calculate the probability of each horse moving forward, you need to understand the sample space, which includes all of the possible outcomes.
Looking at one dice is simpler. There are 6 possible outcomes: 1, 2, 3, 4, 5, 6.Assuming that you are using a dice, each event is equally likely, so the theoretical probability of getting a 6 (or any other score) on a dice is:
When looking at two dice, it gets a bit more complicated as you can get 1, 2, 3, 4, 5, 6 on each of the two dice. So you have to consider all of the possible combinations and the resulting scores.
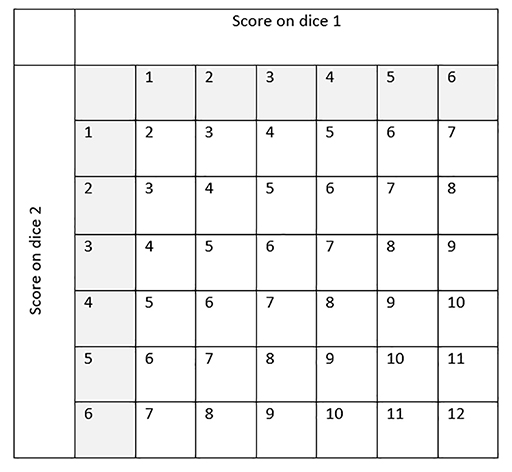
The sample space diagram in Figure 36 shows all of the possible combinations of scores.
Note: the smallest score is 2, since it is not possible to get a score of 1 using two dice.
From the sample space diagram, you can see that there are 36 possible outcomes when rolling two dice. The probability of each event is not 1 in36 though. Some events are more likely than others.
For example, a score of 4 can be made in three ways: 3 then 1, 2 then 2, or 1 then 3, whereas a score of 2 can only be made in one way.
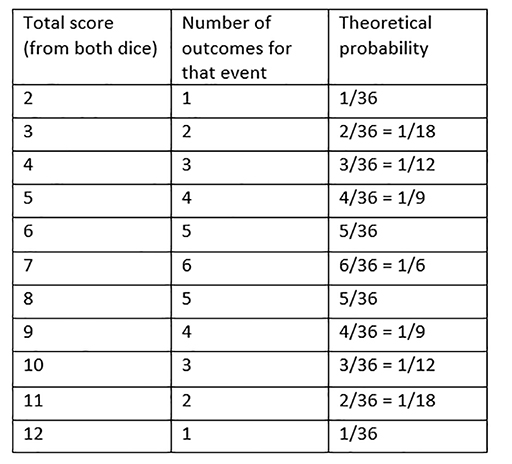
Figure 37 lists the frequency of each event in the sample space. We will use this to calculate the theoretical probability.
Since there are 36 possible outcomes, the theoretical probability for each event will be: