2.1 Area of simple shapes
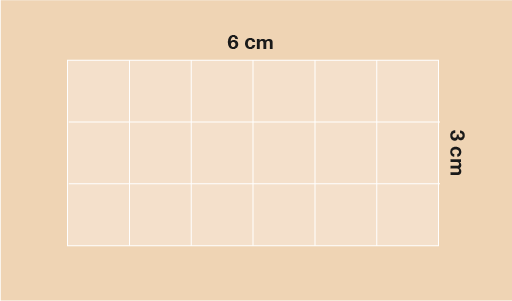
The simplest shapes to begin with when looking at area are squares and rectangles. If you look at the rectangle below you can see that it’s 6 cm long and 3 cm wide. If you count the squares, there are 18 of them. The area of the shape is 18 cm2.
It is not always possible (or practical) to count the squares in a shape or space but it’s a useful illustration to help you understand what area is. More practically, to find the area, (A) of a square or a rectangle, you would multiply the base by the height.
In the example below A = 6 × 3 = 18 cm2.
Triangles are another shape that you can find the area of relatively simply. If you think of a triangle, it is really just half of a rectangle. This is most easy to see with a right-angled triangle as shown below. You can see that the actual triangle (in yellow) is simply a rectangle that has been diagonally cut in half.
In order to find the area of the triangle then, you simply multiply the base by the height (as you would for a rectangle) and then halve the answer.
Sometimes this is shown as the formula:
- A = (b × h) ÷ 2
where b is the base of the triangle and h is the vertical height.
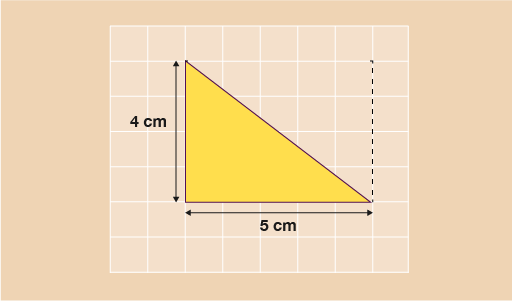
For the triangle below then, you would do:
- A = (5 × 4) ÷ 2
- A = 20 ÷ 2
- A = 10 cm2
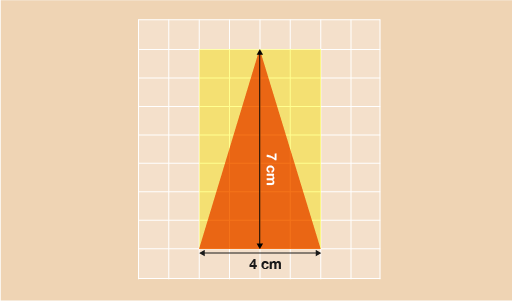
This formula remains the same for any triangle. Take a look at the triangle below. It’s a bit less obvious than with the example above but if you were to take the two yellow sections way and put them together, you would end up with a shape exactly the same size as the orange triangle. The area of this triangle can be found in the same way as the previous one:
- A = (b × h) ÷ 2
- A = (4 × 7) ÷ 2
- A = 28 ÷ 2
- A = 14 cm2
The last basic shape you learn to find the area of is the trapezium. You will need to use a simple formula for this shape (don’t panic when you see it, it looks scary but it really is quite easy to use!)
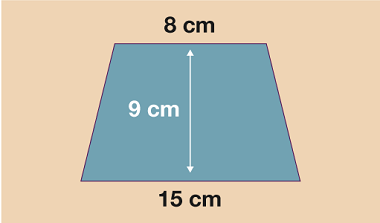
A trapezium looks like any of the shapes below.

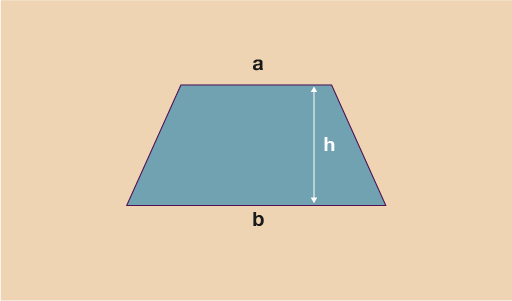
In order to work out the area of a trapezium you just need to know the vertical height and the length of the top and bottom sides. Traditionally, the length of the top is called ‘a’, the length on the bottom is ‘b’ and the vertical height is ‘h’. Once this is clear you can then use the formula:
A =
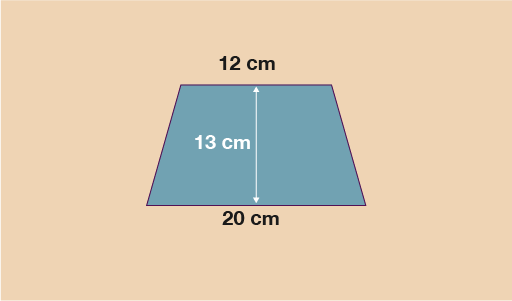
Let’s take a look at an example on how to work out the area of the trapezium below. We can see that the top length (a) = 12 cm. The bottom length (b) = 20 cm, and the height (h) = 13 cm.
Using these values and the formula:
A =
A =
A =
A = 208 cm2
Now that you have seen how to work out the area of several basic shapes, it’s time to put your skills to the test. Have a go at the activity below. Don’t forget that, just as with perimeter, before you can begin any calculations you must make sure all measurements are in the same units.
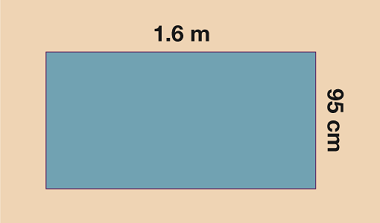
Activity 4: Finding the area
Answer
- If working in cm: 1.6 m = 160 cm, so A = 160 × 95 = 15,200 cm2
If working in m: 95 cm = 0.95 m, so A = 1.6 × 0.95 = 1.52 m2
Answer
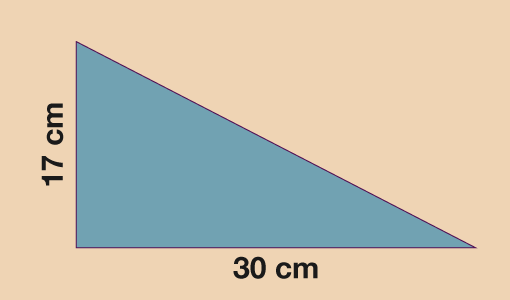
- The two measurements we need for the triangle are the base (30 cm) and the vertical height (17 cm). Don’t be fooled by the diagonal length of 46 cm, you do not need it for the area!
- A = (b × h) ÷ 2
- A = (30 × 17) ÷ 2
- A = 510 ÷ 2
- A = 255 cm2
Answer
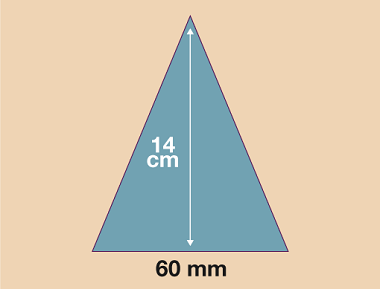
- If working in mm: 14 cm = 140 mm
- A = (b × h) ÷ 2
- A = (60 × 140) ÷ 2
- A = 8400 ÷ 2
- A = 4200 mm2
- If working in cm: 60 mm = 6 cm
- A = (b × h) ÷ 2
- A = (6 × 14) ÷ 2
- A = 84 ÷ 2
- A = 42 cm2
Now that you’ve mastered finding the area of basic shapes, it’s time to look at compound shapes.
A compound shape is just a shape that is made from more than one basic shape. Rarely will you find a floor space, garden area or wall that is perfectly rectangular. More often than not it will be a combination of shapes. The good news is that, to find the area of compound shapes, you simply split them up into their basic shapes, find the area of each of these, and then add them up at the end!