3 Volume
The volume of a shape is how much space it takes up. You might need to calculate the volume of a space or shape if, for example, you wanted to know how much soil to buy to fill a planting box or how much concrete you need to complete your patio.
You’ll need your area skills in order to calculate the volume of a shape. In fact, as you already know how to calculate the area of most shapes, you are one simple step away from being able to find the volume of most shapes too!
Transcript
In this video, you'll look at how to calculate the volume of prisms. A prism is a 3D shape where the cross section, or slice, of the shape is the same all the way through. You can see that a slice of any of these shapes would remain the same wherever you cut it. To calculate the volume of any prism, all you need to do is find the area of the cross section and then multiply this area by the length of the prism.
In this example, you firstly need to calculate the area of the rectangular cross section. 12 times 10 gives an area of 120 centimetres squared. Now you know the area of the cross section, all you need to do is multiply it by the length of the shape: 5 centimetres. Volume equals 120 times 5, which equals 600 centimetres cubed.
Let's try again with a different shape. Here, the cross section is the triangle. You'll recall from your earlier work that to find the area of a triangle, you use this formula. So the area of this cross section is 6 times 5, divided by 2. That is 30 divided by 2. This gives an area of 15 centimetres squared. Now, multiply the area of the cross section by the length of the shape to find the volume. 15 times 12 gives a volume of 180 centimetres cubed. Look at a couple more examples of calculating the volume of prisms, before having a go yourself.
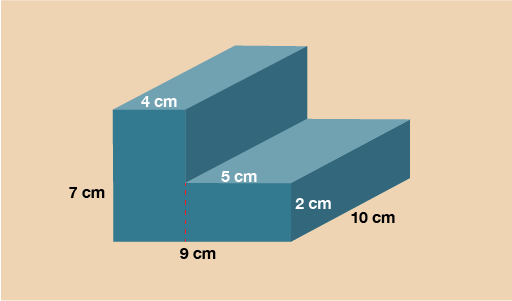
Example: Calculating volume 1
The cross section on this shape is the L shape on the front. In order to work out the area you’ll need to split it up into two rectangles as you practised in the previous part of this section.
Splitting vertically:
Rectangle 1 = 7 × 4 = 28 cm2
Rectangle 2 = 5 × 2 = 10 cm2
Area of cross section = 28 + 10 = 38 cm2
Now you have the area of the cross section, multiply this by the length to calculate the volume.
V = 38 × 10 = 380 cm3
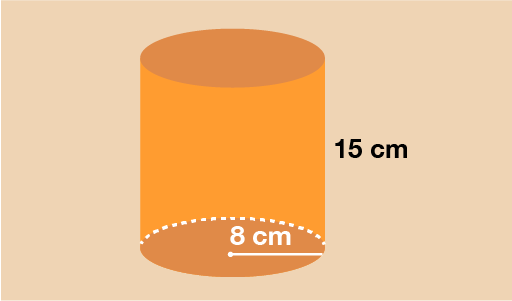
Example: Calculating volume 2
The last example to look at is a cylinder. The cross section of this shape is a circle. You’ll need to use the formula to find the area of a circle in the same way you did in the previous part of this section.
You can see that the circular cross section has a radius of 8 cm. To find the area of this circle, use the formula:
A = πr2
A = 3.142 × 8 × 8
A = 201.088 cm2
Now you have the area, multiply this by the length of the cylinder to calculate the volume.
V = 201.088 × 15 = 3016.32 cm3
Now try yourself in the activity below.
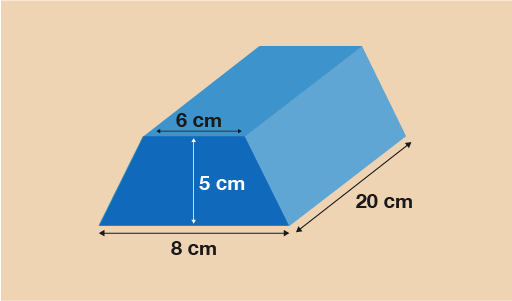
Activity 7: Calculating prism volume
Work out the volume of the 3D trapezium (trapezoidal prism) shown below.
Hint: Go back to the section on area and remind yourself of the formula to find the area of a trapezium.
Answer
The cross section is a trapezium so you will need the formula:
A =- A =
- A =
- A =
- A = 35 cm2
Now you have the area of the cross section, multiply it by the length of the prism to calculate the volume.
- V = 35 × 20 = 700 cm3
The final part of this session will look at scale drawings and plans. It will require your previous knowledge of ratio as scale drawings are really just another application of ratio.
Summary
In this section you have learned:
- that volume is the space inside a 3D shape or space
- how to find the volume of prisms such as cuboids, cylinders and triangular prisms.