3 Around the edge
When might you need to work out how far it is around a flat shape?
You will need to know how far it is around the edge of a shape when you want to put a border around something, such as a wallpaper border around a room, or a brick wall around a patio. You might have thought of different examples.
The distance around any shape is called the perimeter. You can work out the perimeter by adding up all of the sides. The sides are measured in units of length or distance, such as centimetres, metres or kilometres. When you calculate the perimeter of a shape, you need to make sure that all of the measurements are in the same units, converting if necessary.
Example: A length of ribbon
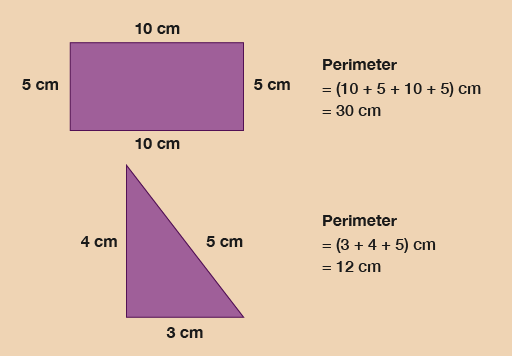
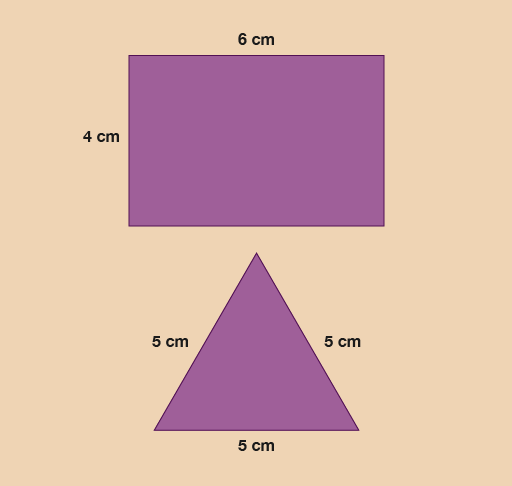
Have a look at Figure 15 to work out how much decorative ribbon you need to go around each shape.
Method
You need to measure all the sides and add them together.
Hint: Opposite sides of a rectangle are the same length.
The sides of the rectangular box are:
6 + 6 + 4 + 4 = 20 cm
You will need 20 cm of ribbon.
The sides of the triangular box are:
5 + 5 + 5 = 15 cm
You will need 15 cm of ribbon.
Example: Lawn edging
So far when you have been working out the perimeter of a rectangle you have added up all four sides. However, there is a quicker way of calculating the perimeter. You may have recognised that all rectangles have two equal short sides and two equal long sides. Therefore you can then work out the perimeter of a rectangle by using each number twice.
(2 × long side) + (2 × short side) = perimeter
The long side is the length. The short side is the width.
(A square is a type of rectangle where all four sides are the same length. So to find out the perimeter of a square, you need to multiply the length of one side by 4.)
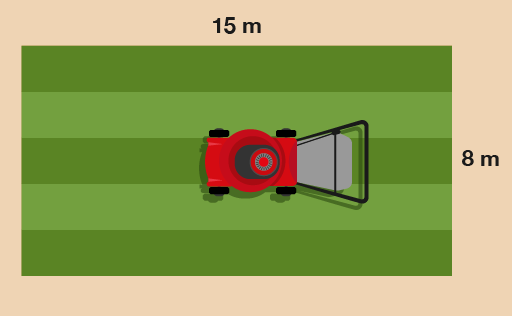
How many metres of lawn edging do you need to go around this lawn?
Method
You need to work out twice the width, plus twice the length:
(2 × 15) + (2 × 8)
Once you’ve worked these out, it makes the answer to the question easier to get:
(2 × 15) + (2 × 8) = 30 + 16 = 46 m
Now try the following activity. Remember to check your answers once you have completed the questions.
Activity 7: Finding the perimeter
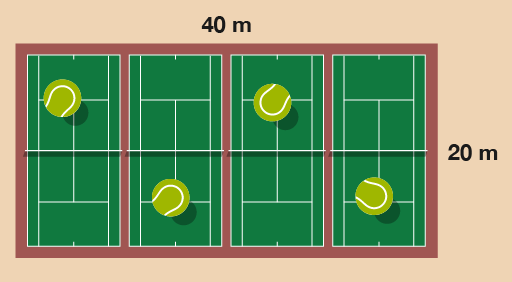
- You need to hang bunting around the tennis courts for the local championships. How much bunting do you need?
- Jackie wants to put a fence around her vegetable garden. Her garden is rectangular in shape and is 5 metres long by 4 metres wide. What length of fence is needed?
Answer
-
The sides of the tennis courts are 20 m and 40 m.
- (2 × 20) + (2 × 40) = 40 + 80 = 120
So 120 m of bunting will be needed.
-
The sides of the garden are 5 m and 4 m.
- (2 × 5) + (2 × 4) = 10 + 8 = 18
So 18 m of fencing will be needed.