3.1 Calculating with time and timetables
As previously discussed, calculators are not the most useful items when it comes to calculations involving time. A much better option is to use a number line to work out these calculations. Take a look at the examples below.
Example: Cooking
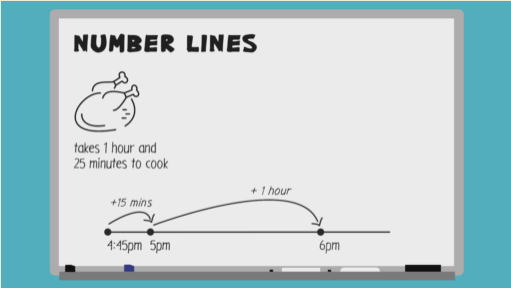
You put a chicken in the oven at 4:45 pm. You know it needs to cook for 1 hour and 25 minutes. What time should you take the chicken out?
Method
Watch the video below to see how the number line method works.
Transcript
A chicken takes 1 hour and 25 minutes to cook. So, to work out when the chicken will be ready, you can use a number line, which looks like this. The idea behind the number line is that we use small, easy chunks of time to work out the answer. In this example, you know that you need to add 1 hour and 25 minutes onto 4:45 p.m. Here is a number line that starts at 4:45 p.m.
To begin with, add 15 minutes, since this will take us to an easy time of 5:00 p.m. It then makes sense to add an hour on, which takes you to 6:00 p.m. As you've now added 1 hour and 15 minutes, you still need to add another 10 minutes. This takes you to 6:10 p.m., which is when the chicken will be ready. There's no exact science to using the number line for calculations like these. You just add on in chunks of time to make the calculation simpler.
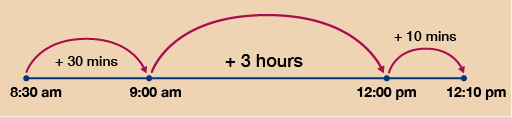
Example: Time sheets
You work for a landscaping company and need to fill out your time sheet for your employer. You began working at 8:30 am and finished the job at 12:10 pm. How long did the job take?
Method
Again, for finding the time difference you want to work with easy ‘chunks’ of time. Firstly, you can move from 8:30 am to 9:00 am by adding 30 minutes. It is then simple to get to 12:00 pm by adding on 3 hours.
Finally, you just need another 10 minutes to take you to 12:10 pm. Looking at the total time added you have 3 hours and 40 minutes.
Another aspect of calculating with time comes in the form of timetables. You will be used to using these to work out which departure time you need to meet in order to get to a location on time or how long a journey will take. Once you can calculate with time, using timetables simply requires you to find the correct information before carrying out the calculation. Take a look at the example below.
Example: Timetables
Here is part of a train timetable from Swindon to London.
| Swindon | 06:10 | 06:27 | 06:41 | 06:58 | 07:01 | 07:17 |
|---|---|---|---|---|---|---|
| Didcot | 06:27 | 06:45 | 06:58 | 07:15 | 07:18 | 07:34 |
| Reading | 06:41 | 06:59 | 07:13 | - | 07:33 | - |
| London | 07:16 | 07:32 | 07:44 | 08:02 | 08:07 | 08:14 |
- a.You need to travel from Didcot to London. You need to arrive in London by 8:00 am. What is the latest train you can catch from Didcot to arrive in London for 8:00 am?
Method
| Swindon | 06:10 | 06:27 | 06:41 | 06:58 | 07:01 | 07:17 |
|---|---|---|---|---|---|---|
| Didcot | 06:27 | 06:45 | 06:58 | 07:15 | 07:18 | 07:34 |
| Reading | 06:41 | 06:59 | 07:13 | - | 07:33 | - |
| London | 07:16 | 07:32 | 07:44 | 08:02 | 08:07 | 08:14 |
Looking at the arrival times in London, in order to get there for 8:00 am you will need to take the train that arrives in London at 07:44 (highlighted with bold). If you then move up this column of the timetable you can see that this train leaves Didcot at 06:58 (highlighted with italic). This is therefore the train you must catch.
- b.How long does the 06:58 from Swindon take to travel to London?
Method
| Swindon | 06:10 | 06:27 | 06:41 | 06:58 | 07:01 | 07:17 |
|---|---|---|---|---|---|---|
| Didcot | 06:27 | 06:45 | 06:58 | 07:15 | 07:18 | 07:34 |
| Reading | 06:41 | 06:59 | 07:13 | - | 07:33 | - |
| London | 07:16 | 07:32 | 07:44 | 08:02 | 08:07 | 08:14 |
Firstly, find the correct train from Swindon (highlighted with italic). Follow this column of the timetable down until you reach London (highlighted with bold). You then need to find the difference in time between 06:58 and 08:02. Using the number line method from earlier in the section (or any other method you choose).
You can then see that this train takes a total of 1 hour and 4 minutes to travel from Swindon to London.
Have a go at the activity below to practise calculating time and using timetables.
Activity 6: Timetables and calculating time
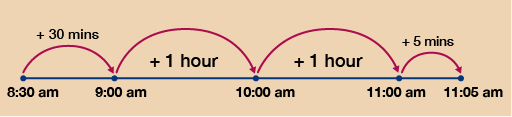
Kacper is a builder. He leaves home at 8:30 am and drives to the trade centre. He collects his items and loads them into his van. His visit takes 1 hour and 45 minutes. He then drives to work, which takes 50 minutes. What time does he arrive at work?
You have invited some friends round for dinner and find a recipe for roast lamb. The recipe requires:
- 25 minutes preparation time
- 1 hour cooking time
- 20 minutes resting time
You want to eat with your friends at 7:30 pm. What is the latest time you can start preparing the lamb?
Here is part of a train timetable from Manchester to Liverpool.
| Manchester to Liverpool | ||||||
|---|---|---|---|---|---|---|
| Manchester | 10:24 | 10:52 | 11:03 | 11:25 | 12:01 | 12:13 |
| Warrington | 10:38 | 11:06 | 11:20 | 11:45 | 12:15 | 12:28 |
| Widnes | 10:58 | 11:26 | 11:42 | 12:03 | 12:34 | 12:49 |
| Liverpool Lime Street | 11:09 | 11:38 | 11:53 | 12:14 | 12:46 | 13:02 |
You need to travel from Manchester to Liverpool Lime Street. You need to be in Liverpool by 12:30. Which train should you catch from Manchester and how long will your journey take?
Answer
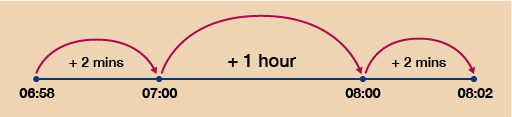
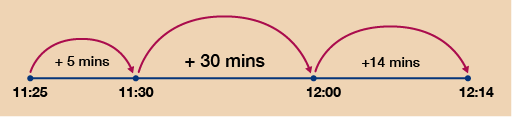
- Firstly, work out the total time that Kacper is out for:
- 1 hour 45 minutes at the trade centre and another 50 minutes driving makes a total of 2 hours and 35 minutes.
Then, using the number line, you have:
So Kacper arrives at work at 11:05 am.
You could also do the calculation by adding on the 1 hour 45 minutes first:
- 8:30 am + 1 hour = 9:30 am
- 9:30 am + 45 minutes = 10:15 am
Finally, you can add on the 50 minutes:
- 10:15 am + 45 minutes = 11:00 am
Then add on the remaining 5 minutes:
- 11:00 am + 5 minutes = 11:05 am
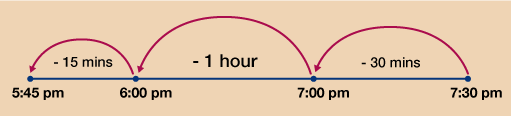
- Again, firstly work out the total time required:
- 25 minutes + 1 hour + 20 minutes = 1 hour 45 minutes in total
This time you need to work backwards on the number line so you begin at 7:30 and work backwards.
You can now see that you must begin preparing the lamb at 5:45 pm at the latest.
As with the first question, you could have done this question by taking off each stage in the cooking process separately rather than finding the total time first:
- 7:30 pm − 20 minutes = 7:10 pm
- 7:10 pm − 1 hour = 6:10 pm
There are 25 minutes left so:
- 6:10 pm − 10 minutes = 6:00 pm
There are now 15 minutes left so:
- 6:00 pm − 15 minutes = 5:45 pm
- Looking at the timetable for arrival at Liverpool, you can see that in order to arrive by 12:30 you need to catch the train that arrives at 12:14. This means that you need to catch the 11:25 from Manchester.
| Manchester to Liverpool | ||||||
|---|---|---|---|---|---|---|
| Manchester | 10:24 | 10:52 | 11:03 | 11:25 | 12:01 | 12:13 |
| Warrington | 10:38 | 11:06 | 11:20 | 11:45 | 12:15 | 12:28 |
| Widnes | 10:58 | 11:26 | 11:42 | 12:03 | 12:34 | 12:49 |
| Liverpool Lime Street | 11:09 | 11:38 | 11:53 | 12:14 | 12:46 | 13:02 |
You therefore need to work out the difference in time between 11:25 (italic) and 12:14 (bold).
Using the number line again, you can see that this is a total of 5 + 30 + 14 = 49 minutes.
You should now be feeling comfortable with calculations involving time and timetables. Before you move on to looking at problems that involve average speed, it is worth taking a brief look at time conversions. Since you are already confident with converting units of measure, this part will just consist of a brief activity so that you can practise converting units of time.