10.3 Solving ratio problems where the total of one part of the ratio is given
Take a look at the worked example below:
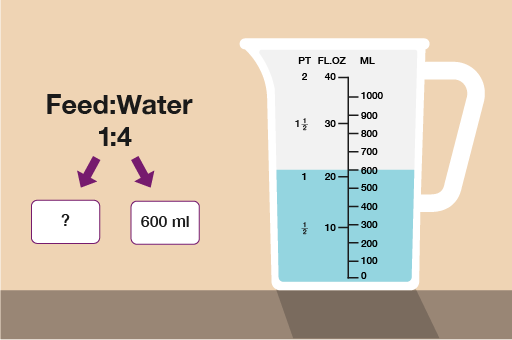
You are growing tomatoes. The instructions on the tomato feed say:
- Use 1 part feed to 4 parts water
If you use 600 ml of water, how much tomato feed should you use?
These questions make much more sense if you look at them visually:
You can now see clearly that 600 ml of water is worth 4 parts of the ratio. To find one part of the ratio you need to do:
- 600 ml ÷ 4 = 150 ml
Since the feed is only 1 part, feed must be 150 ml. If feed was more than one part you would multiply 150 ml by the number of parts.
Just as with the previous type of question, you need to try to work out the value of 1 part. The value of any other number of parts can be worked out from this.
Activity 26: Ratio problems with one part given
Practise your skills by tackling the ratio problems below:
A recipe requires flour and butter to be used in the ratio 3:5. The amount of butter used is 700 g.
How much flour will be needed?
When looking after children aged between 7 and 10, the ratio of adults to children must be 1:8.
- a.For a group of 32 children, how many adults must there be?
- b.If there was one more child in the group, how would this affect the number of adults required?
Answer
- Adults:Children
- a.
To find one part you do 32 ÷ 8 = 4.
Since adults are only 1 part, you need 4 adults.
b.If there were 33 children, one part would be 33 ÷ 8 = 4.125.
Since you cannot have 4.125 adults, you need to round up to 5 adults so you would need one more adult for 33 children.
- a.
A shop mixes bags of muesli using oats, sultanas and nuts in the ratio 6:3:1.
If the amount of sultanas used is 210 g, how heavy will the bag of muesli be?
Answer
Oats:Sultanas:Nuts
 Figure 18 Working out the ratio of oats, sultanas and nuts
Figure 18 Working out the ratio of oats, sultanas and nutsSultanas are 3 parts so to find 1 part you do 210 g ÷ 3 = 70 g.
Oats are 6 parts so 6 × 70 = 420 g.
Nuts are only 1 part so they are 70 g.
The total weight of the bag would be 210 g + 420 g + 70 g = 700 g.
Next you’ll look at ratio problems where only the difference in amounts is given.