2 Combining sets

Figure 10 Some purple sheep

Show description|Hide description

A picture of approximately 10 sheep standing at the top of a hill. The sheep have purple-coloured coats.

Figure 10 Some purple sheep

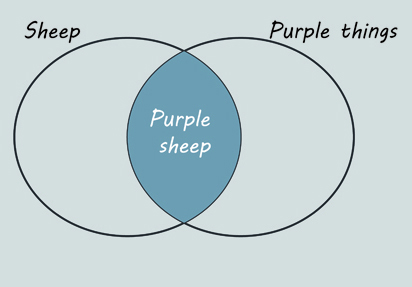
The Euler diagrams you saw in Section 1 showed sets containing other sets, and sets that did not overlap other sets. But, of course, it is common for two sets to share some members. Consider the example of purple sheep (Figure 10).

Figure 11 shows two sets: the set of sheep, and the set of things that are purple. The overlapping area represents the set of purple sheep. This is called the intersection of the sets.

Figure 11 The intersection of Sheep and Purple things is Purple sheep

Show description|Hide description

Some sheep whose coats have been dyed purple stand on a hillside.

Figure 11 The intersection of Sheep and Purple things is Purple sheep

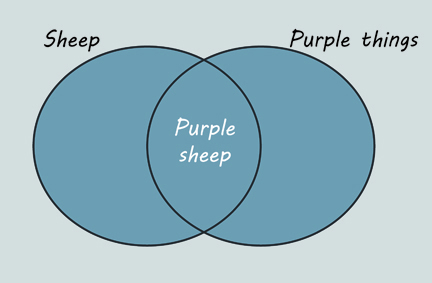
Another way to combine two sets is to join them together and take all the objects that are in the first set, the second set, or both. This is called the union (Figure 12).

Figure 12 The union of Sheep and Purple things is things that are Sheep, or Purple, or both.

Show description|Hide description

The union of Sheep and Purple things is things that are Sheep, or Purple, or both.

Figure 12 The union of Sheep and Purple things is things that are Sheep, or Purple, or both.

A common way to list the members of a set is between ‘curly brackets’, also called braces. You could write:

sheep = {'agnes', 'wilhemina', 'rusty', 'billy', 'leaper'}

purple_things = {'rusty', 'aubergine', 'amethyst', 'leaper'}

The intersection of 'sheep' and 'purple_things' would be

{'rusty', 'leaper'}

and the union would be

{'agnes', 'wilhemina', 'rusty', 'billy', 'leaper', 'aubergine', 'amethyst'}

These are not sets of real objects but of words. However, sets of real objects have intersections and unions in the same way as these examples.

There are two important points to note about sets.

• No member of a set can appear more than once.
• The order in which the members of a set are listed is irrelevant. It is still the same set whatever the order.

Python has sets and can calculate intersections and unions. In the interactive shell below execute the following lines.

>>> sheep = {'agnes', 'wilhemina', 'rusty', 'billy', 'leaper'}

>>> purple_things = {'rusty', 'aubergine', 'amethyst', 'leaper'}

Now enter

>>> sheep

and

>>> purple_things

and you will see that Python has remembered the sets.

To calculate the intersection, you use the & symbol. Enter

>>> sheep & purple_things

and you will see the expected set

{'rusty', 'leaper'}

For the union, you use the | symbol. Enter

>>> sheep | purple_things

and you will see the expected result

{'agnes', 'wilhemina', 'rusty', 'billy', 'leaper', 'aubergine', 'amethyst'}.

The next section explains how to find the size of a set.