1.1 Pascal’s triangle
Numbering the tiles in Activity 1 gave a number pattern that described a geometric pattern. This next example is a number pattern that appeared in China and Persia more than 700 years ago, but is still used by students in mathematical and statistical problems today – it even appears in chemistry. It is known as ‘Pascal’s triangle’ after the French mathematician Blaise Pascal who studied the properties of this triangle. The first part of Pascal’s triangle is shown in Figure 2:
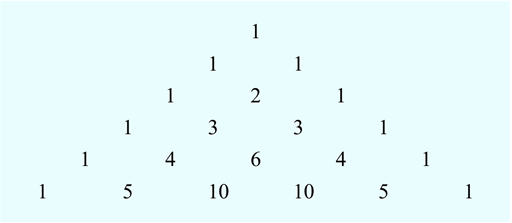
You can continue the triangle indefinitely by following the pattern. So how is it created?
If you look at the triangle you can see that each row of numbers starts and ends with the number 1. Now look at the numbers in the second to last line (1 4 6 4 1) and the last line of the triangle. Look carefully at them both - can you see a way that you can make the numbers in the last line from the line above? If you add each pair of numbers in the second to last line, this gives you numbers in the last line.
Starting from the left-hand side the pairs of numbers are 1 and 4, 4 and 6, 6 and 4, and 4 and 1. So:
This process, plus adding a 1 at end of the line, generates the next row of the triangle. Have a go at creating the next line for yourself in this next activity.
Activity _unit4.1.2 Activity 2 Pascal’s triangle – next line
Create the next line of Pascal’s triangle by adding the pairs of numbers in the last line. Remember to add the 1s to the end of the rows when you are done.
Answer
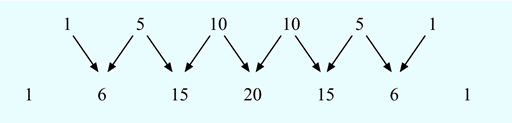
Starting from the left-hand side the pairs of numbers are 1 and 5, 5 and 10, 10 and 10, 10 and 5, and lastly 5 and 1.
Adding these pairs gives us:
So the next line in the triangle should look like the bottom one in Figure 3:
You can watch a larger version of Pascal’s triangle being built in this video:
Now you’ve seen how to build Pascal’s triangle by adding pairs of numbers it’s time to see if there are more patterns hiding in this number triangle in the next section.
