3 Areas
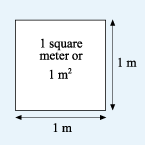
If someone is planning to paint a wall, one of the first questions to ask will be how much paint they need. This will obviously depend on the size of the wall and how many coats needed. Fortunately, paint cans usually include information about the area that the paint will cover. For example, on the back of a 2.5-litre can of emulsion paint, it says that the paint will cover ‘up to 35 square metres.’ A square metre is the area that is covered by a square whose sides measure 1 m, as shown in Figure 16. This can also be written as 1 m2. So 35 m2 will be the same area as the area of 35 of these 1-metre squares.
Areas can also be measured in other square units, such as square centimetres (cm2) or square kilometres (km2), depending on what is appropriate to the situation. For example, if you wanted the area of a country, it would not make sense to show this in cm2 or m2 as the value would be very large! Similarly to a square metre, a square centimetre is a square whose sides are 1 cm long, and a square kilometre has sides that are 1 km long. If the diagram below (Figure 17) is drawn on a grid in which the lines are 1 cm apart, then each grid square will have an area of 1 cm2. One way to work out the total area is counting the number of these squares. This gives us 16, so the grid shown is 16 cm2 altogether.
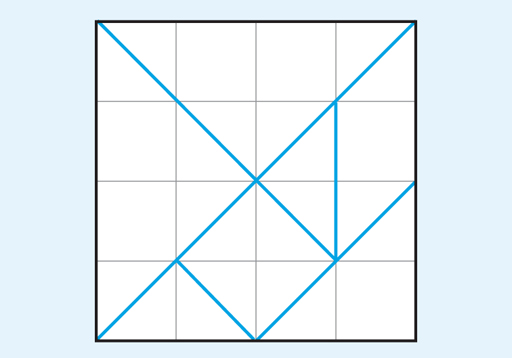
You can use the same technique to determine the areas of the shapes shown on the diagram. Try this now in the next activity.
Activity _unit7.3.1 Activity 5 Counting squares
All the shapes on the diagram in Figure 17 are made up out of whole squares or half squares. Use this information to work out the areas of each of the shapes.
Answer
The areas in square centimetres are shown in Figure 18:
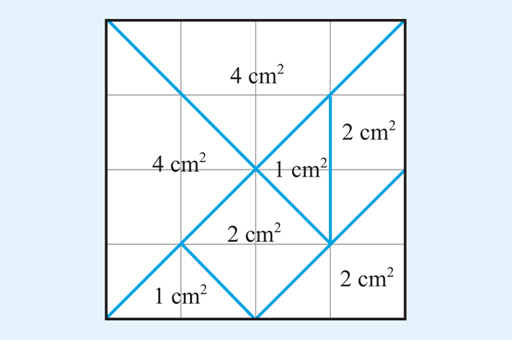
Let’s take the top triangle as an example to show how this was worked out.
This triangle is made up of two full squares and four half squares. Four half squares are the same as 2 full squares, so the total area of the top triangle is 4 cm2.
To check the answers, you can add the individual areas and see if they total 16 cm2.
The sum of the individual areas in cm2 = 4 + 4 + 1 + 2 + 1 + 2 + 2 = 16.
This gives confidence in the individual answers and acts as a very useful check.
Counting squares is one way to work out the area of shapes, particularly if they are irregular. However, it is not very convenient in a lot of situations so this is where the power of formulas comes into play once again.
