3.2 Finding an area using formulas
Figure 23 is a rough sketch of the gable end of a house that needs weatherproofing.
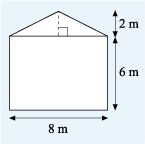
To work out the quantity of materials required, the area of the wall is needed. This problem can be broken down by splitting the area into a rectangle and a triangle, then working out these areas and finally adding the two areas together to get the total.
The triangle has a base of length 8 m and a perpendicular height of 2 m. So, the area can be calculated as follows:
That means the total area of the gable end = 48 m2 + 8 m2.
Now, it’s your turn to put what you’ve learned in this section to use.
Activity _unit7.3.2 Activity 6 Using formulas to calculate areas
Figure 24 shows the same diagram as you have already seen in previous activities. This time though, instead of counting the squares to determine the areas, use the relevant formulas from the previous section. Remember that the whole grid measures 4 cm by 4 cm, and each small square is 1 cm by 1 cm.
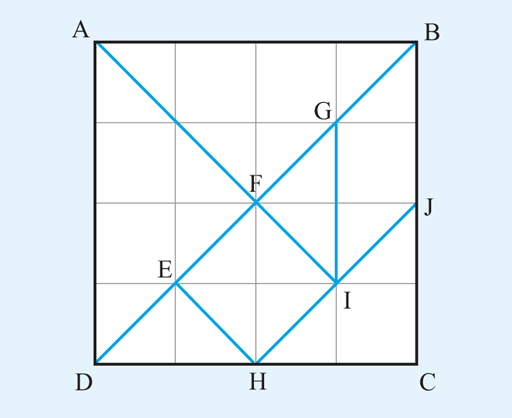
Calculate the areas of the following shapes.
- a.Triangle ADF with AD as the base
Answer
a.The base of the triangle is AD. AD = 4 cm.
The perpendicular height from F onto AD = 2 cm.
- b.Parallelogram GBJI with BJ as the base
Answer
b.BJ = 2 cm. The perpendicular height from G onto BJ = 1 cm.
Now that you know how to calculate the areas of basic shapes, you can calculate more complicated areas by breaking each shape into basic shapes and adding the individual areas together.
Many area problems can be calculated by using combinations of squares, rectangles and triangles. However, you often need to find circular areas, too. The next section will cover this aspect of areas.
