Interpreting data: boxplots and tables
Use 'Print preview' to check the number of pages and printer settings.
Print functionality varies between browsers.
Printable page generated Tuesday, 23 April 2024, 6:08 PM
Interpreting data: boxplots and tables
Introduction
This course is concerned with two main topics. In Section 1, you will learn about another kind of graphical display, the boxplot. Boxplots are particularly useful for assessing quickly the location, dispersion, and symmetry or skewness of a set of data, and for making comparisons of these features in two or more data sets. The other topic, is that of dealing with data presented in tabular form. You are, no doubt, familiar with such tables: they are common in the media and in reports and other documents. It is not always straightforward to see at first glance just what information a table of data is providing, and it often helps to carry out certain calculations and/or to draw appropriate graphs to make this clearer.
This OpenLearn course is an adapted extract from the Open University course M248 Analysing data.
Learning outcomes
After studying this course, you should be able to:
understand and use the following terms: boxplots, box, whisker, upper and lower adjacent values, rate, time series, line plot
demonstrate an awareness of the idea that the general pattern of a set of data, in terms of location, dispersion and skewness, can be graphically represented in a boxplot
understand that boxplots can be used to provide a quick and simple comparison of data sets
understand that patterns in tabular data can be made clearer by leaving out unhelpful information, by including extra pieces of useful information, or by drawing appropriate graphs
describe and compare data sets on the basis of boxplots.
Overview
It is a common observation that a data exploration should always begin by looking at a graphical display of the data. When looking at data sets which involve only one variable, displays such as bar charts and histograms are available. One problem with these is that they can include too much detail. Also they are not very useful for comparing two or more samples of data. A graphical display showing certain summary statistics in a visually appealing and interpretable way is introduced in this section. This is the boxplot.
1 Boxplots
In this first section, you will learn how to construct a boxplot for a single set of data. The use of boxplots to compare two or more sets of data will then be discussed.
1.1 Simple boxplots
A boxplot is simple to construct. The following example on the β endorphin concentrations of collapsed runners will be used to show how this is done.
Example 1.1 Endorphin concentrations for collapsed runners
The β endorphin concentrations (in pmol/l) recorded for eleven runners who collapsed after the Great North Run are as follows (written in order of increasing size).
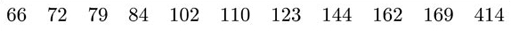
A boxplot for these data is shown in Figure 1.1.

Figure 1.1 A boxplot for the collapsed runners
(Data sourced from Dale, G., Fleetwood, J.A., Weddell, A., Ellis, R.D. and Sainsbury, J.R.C. (1987) Beta-endorphin: a factor in 'fun run' collapse? British Medical Journal, 294, 1004.)
The easiest way to understand exactly what a boxplot represents and how it is constructed is to think about how you would draw one by hand. The steps involved in constructing the boxplot in Figure 1.1 for the data set of β endorphin concentrations are as follows.
First, a convenient scale is drawn covering the extent of the data. Since the minimum is 66 and the maximum is 414, a scale from 0 to 500 (say) is suitable in this case. The boxplot is drawn against this scale.
The median and quartiles are used to construct the ‘box’. The median of this data set is 110, and the lower and upper quartiles are 79 and 162, respectively. The box is shown in Figure 1.2.
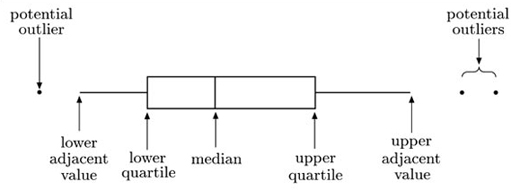
The ‘box’ is a rectangle with edges defined by the lower and upper quartiles; so it indicates where the ‘middle 50%’ of the data can be found. The vertical line inside the box is located at the median.
The ‘whiskers’ are constructed next. These are lines drawn parallel to the scale (so they are horizontal in this course). Essentially, each whisker extends outwards from the edge of the box as far as the most extreme observation. However, as you will see in the next step, some observations may be classified as potential outliers; and in fact the whiskers extend only to cover observations which are not classified as potential outliers. The whiskers are drawn outwards as far as observations called adjacent values. The lower adjacent value is the furthest observation which is within one and a half iqr (interquartile range) of the lower end of the box; and the upper adjacent value is the furthest observation which is within one and a half iqr of the upper end of the box. So the interquartile range is needed to construct the whiskers.
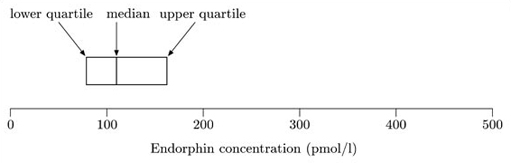
Figure 1.2 Collapsed runners boxplot: the box
For these data, the interquartile range is 162−79=83. So
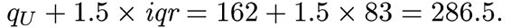
The highest observation not exceeding 286.5 is 169, so the upper adjacent value is 169, and hence the right-hand whisker extends as far as the observation 169. Similarly,
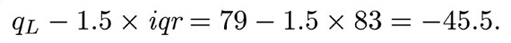
The lowest observation, 66, is greater than this, so the lower adjacent value is 66, and the left-hand whisker extends to 66. Notice that, in this example, the lower adjacent value is the same as the sample minimum, 66. Figure 1.3 shows the box with the whiskers extending to the upper and lower adjacent values.

Figure 1.3
Finally, any values not covered by the whiskers are marked separately. In some circumstances, they may be deemed outliers. At the least, they are potential outliers and merit special attention.
In this case, the only observation not covered by the whiskers is the maximum observation of 414. This is shown in Figure 1.4.
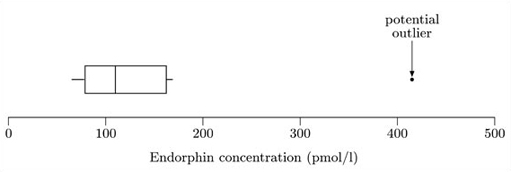
Figure 1.4
It must be stressed that boxplot construction is an area where there are no universally accepted rules. All boxplots show the three quartiles, but the conventions defining the extent of the whiskers vary from text to text and from one computer package to another. The whiskers may extend as low as one or even up to two interquartile ranges either side of the box. Some approaches even distinguish between moderate and severe outliers by using different symbols for them. Some textbooks and software always draw the whiskers right out to the minimum and maximum values and do not mark (potential) outliers separately. The approach adopted here is one of the simplest and is probably the most common.
You can see how a boxplot gives a quick visual assessment of the data. The length of the box represents the interquartile range and the lengths of the whiskers relative to the length of the box give an idea of how stretched out the rest of the values are. Thus these aspects of the diagram give an idea of the dispersion of the data set. The unusually large value in this data set is clearly shown and the median gives an assessment of the centre.
Some kind of assessment of symmetry is possible, since symmetric data will produce a boxplot which is symmetric about the median. These particular data are not symmetric; they are right-skew, and in fact the sample skewness is 2.572. The corresponding lack of symmetry shows up in the boxplot: the right-hand section of the box is longer than the left. However, it should be borne in mind that this particular data set has only eleven values, and this is too small a number to infer anything definite about any underlying structure.
You should now ensure that you understand simple boxplots by constructing one for yourself.
A boxplot displays the median, the quartiles, the range of values covered by the data and any outliers which may be present. It gives a clear picture of all these features and, as you will see, allows a visual appreciation of lack of symmetry.
1.2 Boxplot activity
Activity 1 Drawing a boxplot: chondrite meteors
Table 1.1 contains data on the percentage of silica found in 22 chondrite meteors. The data are given in order of increasing size.
| 20.77 | 22.56 | 22.71 | 22.69 | 26.39 | 27.08 | 27.32 | 27.33 |
| 27.57 | 27.81 | 28.69 | 29.36 | 30.25 | 31.89 | 32.88 | 33.23 |
| 33.28 | 33.40 | 33.52 | 33.83 | 33.95 | 34.82 |
(Source: Good, I.J. and Gaskins, R.A. (1980) Density estimation and bump-hunting by the penalized likelihood method exemplified by scattering and meteorite data. J. American Statistical Association, 75, 42-56.)
The median for this data set is 29.025; the lower and upper quartiles are approximately 26.91 and 33.31. The interquartile range is 6.40.
(a) Using a pencil and ruler, construct a boxplot for these data.
(b) The sample skewness for these data is −0.446. Is this value in accord with the shape of the boxplot?
Answer
Solution
(a) The data run from 20.77 to 34.82. A convenient scale to cover this range of values runs from 20 to 40. In this case,
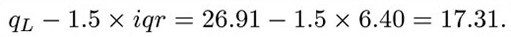
This is smaller than the sample minimum, so the left-hand whisker will extend as far as the minimum observation 20.77. (In other words, the lower adjacent value is equal to the sample minimum.) Similarly,
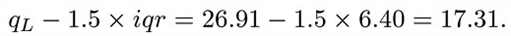
This is greater than the sample maximum, so the upper adjacent value is the same as the sample maximum. So with this data set, there are no extreme values to be plotted separately. The boxplot is shown in Figure 3.1.
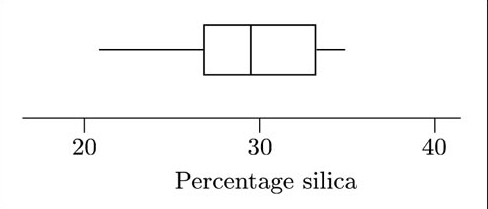
Figure 1.5a
(b) The sample skewness is negative, indicating that the data are left-skew. To some extent the boxplot reflects this: the left whisker is considerably longer than the right, indicating that the smaller values are more spread out than are the larger values. However, the box gives a different impression. The box corresponds to the middle half of the data values, and the line denoting the median divides this into two parts, each corresponding to one-quarter of the data. In this case, the left part of the box is shorter than the right part. In other words, the box suggests that the data might be right-skew rather than left-skew. So the pattern of asymmetry of these data is not straightforward.
In assessing patterns of skewness from a boxplot, you are looking at five different values: the upper and lower adjacent values, the upper and lower quartiles, and the median. It is thus possible, in some cases at least, to observe somewhat complicated patterns of skewness. On the other hand, calculating the sample skewness involves boiling the data down to a single value; and thus the sample skewness provides rather less information than a boxplot does about the shape of a data set.
The boxplot for the data in Table 1.1, which you were asked to draw in Activity 1, is shown in Figure 1.5.
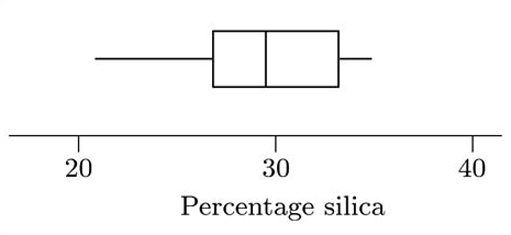
Figure 1.5b
This boxplot is clearly not symmetrical. However, the pattern of its skewness is not straightforward. The box, corresponding to the middle 50% of the data, appears to be right-skew, because the line marking the median is towards the left of the box (so that the right section of the box is longer than the left). However, the longer whisker is on the left, indicating a longer tail towards smaller values, which in turn suggests that the data are left-skew.
In this example, the sample skewness (−0.446) is in accord with the pattern suggested by the whiskers of the boxplot (left-skew), rather than with that suggested by the box. Essentially, this occurs because all the values in the data set are used to calculate the sample skewness; and the calculation involves a sum of powers of values, so that the sample skewness is particularly affected by the more extreme values in the data set. In a boxplot, the whiskers correspond to the more extreme values. In Figure 1.5, the whiskers suggest that the data are left-skew, matching the sample skewness.
1.3 Comparing data sets using boxplots
Example 1.2 Infants with SIRDS: boxplots
Boxplots are particularly useful for making quick comparisons. The following example relates to birth weights of infants exhibiting severe idiopathic respiratory distress syndrome (SIRDS), and the question ‘Is it possible to relate the chances of eventual survival to birth weight?’ The data in Table 1.3 are the recorded birth weights of infants who displayed the syndrome.
| 1.050* | 2.500* | 1.890* | 1.760 | 2.830 |
| 1.175* | 1.030* | 1.940* | 1.930 | 1.410 |
| 1.230* | 1.100* | 2.200* | 2.015 | 1.715 |
| 1.310* | 1.185* | 2.270* | 2.090 | 1.720 |
| 1.500* | 1.225* | 2.440* | 2.600 | 2.040 |
| 1.600* | 1.262* | 2.560* | 2.700 | 2.200 |
| 1.720* | 1.295* | 2.730* | 2.950 | 2.400 |
| 1.750* | 1.300* | 1.130 | 3.160 | 2.550 |
| 1.770* | 1.550* | 1.575 | 3.400 | 2.570 |
| 2.275* | 1.820* | 1.680 | 3.640 | 3.005 |
| *child died | ||||
van Vliet, P.K. and Gupta, J.M. (1973) Sodium bicarbonate in idiopathic respiratory distress syndrome. Arch. Disease in Childhood, 48, 249–255.
An initial investigation of the question might involve histograms of the two sets of birth weights, as well as calculating their sample means, standard deviations and skewnesses. The results in this case would show that the mean birth weight of the infants who survived is considerably higher than the mean birth weight of the infants who died, and that the standard deviation of the birth weights of the infants who survived is also higher. Using boxplots we will now be able to make some further headway with the question.
For the birth weights (in kg) of the infants who survived, the lower quartile, median and upper quartile are, respectively, 1.72, 2.20 and 2.83. For the infants who died, the corresponding quartiles are 1.23, 1.60 and 2.20. Using these figures, together with the original data in Table 1.3 above, boxplots of the two data sets can be constructed. Notice that in both cases (as in Activity 1) the adjacent values are equal to the sample maxima and minima, so that the whiskers extend to the ends of the sample range. Plotting both boxplots against the same scale produces the diagram in Figure 1.6.
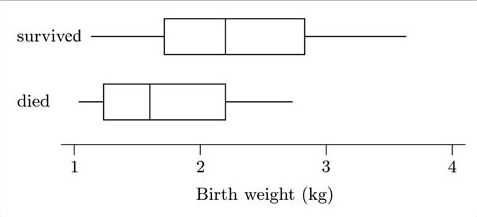
Figure 1.6
As you saw in Subsection 1.1, a boxplot gives graphical information on the location, the dispersion and the skewness of a data set – that is, on the three aspects of the data set for which summary measures were introduced in Unit A1. In addition, a boxplot draws attention to certain potential outliers. Thus comparative boxplots, as in Figure 1.6, can be used to compare these four features in the data sets shown. This has been done in producing the following discussion of the SIRDS data.
Comparison of location: Figure 1.6 shows that the median birth weight of infants who survived is greater than that of those who died.
Comparison of dispersion: The interquartile ranges are reasonably similar (as shown by the lengths of the boxes), though the overall range of the data set is greater for the surviving infants (as shown by the distances between the ends of the two whiskers for each boxplot).
Comparison of skewness: Though both batches of data appear to be right-skew, and the batch for the infants who died is slightly more skewed than that for those who survived, the skewness is not particularly marked in either case. (In fact, the sample skewness for the birth weights of the infants who survived is 0.25; and for the infants who died, it is 0.53. Both skewnesses are positive; the value for the infants who died is rather larger, corresponding to a more marked lack of symmetry, but neither skewness is particularly large.)
Comparison of potential outliers: Neither data set shows any suspiciously far out values which might require a closer look.
General conclusions: Overall, the two batches of data look as if they were generally distributed in a similar way, but with one batch located to the right (larger location) of the other. You can see immediately that the median birth weight of infants who died is less than the lower quartile of the birth weights of infants who survived (that is, over three-quarters of the survivors were heavier than the median birth weight of those who died). So it looks as if we can safely say that survival is related to birth weight.
You can see how comparative boxplots give a compact, quickly assimilated summary of the data, suggesting that infants who survive and infants who do not may typically have different birth weights.
When using boxplots to compare two or more batches of data, it is usually best to compare individual features in a methodical way. You may find the following guidelines helpful.
Guidelines for comparing boxplots
Compare the respective medians, to compare location.
Compare the interquartile ranges (that is, the box lengths), to compare dispersion.
Look at the overall spread as shown by the adjacent values. (This is another aspect of dispersion.)
Look for signs of skewness. If the data do not appear to be symmetric, does each batch show the same kind of asymmetry?
Look for potential outliers.
After discussing these features, general conclusions should be summarized briefly.
Let us look at another example. This time, you are asked to do the work!
1.4 Boxplot activity 2
Activity 2 Boxplots of family sizes
The table below contains data on the sizes (numbers of children) of the completed families of two samples of mothers in Ontario. One sample of mothers had had fewer years of education than the other sample (six years or less for mothers in the first sample, and seven years or more for those in the other sample).
| Mother educated for six years or less |
| 14 13 4 14 10 2 13 5 0 0 13 3 9 2 10 11 13 5 14 |
| Mother educated for seven years or more |
| 0 4 0 2 3 3 0 4 7 1 9 4 3 2 3 2 16 6 0 13 6 6 5 9 10 5 4 3 3 5 2 3 5 15 5 |
Keyfitz, N. (1953) A factorial arrangement of comparisons of family size. American J. Sociology, 53, 470–480.
Comparative boxplots of the family size data are shown in Figure 1.7.
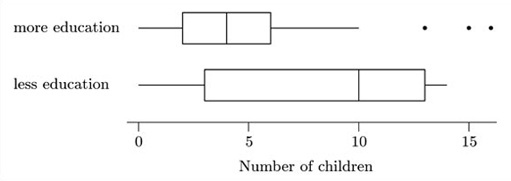
Figure 1.7
Compare the two samples of data using the systematic approach just outlined in the text. What conclusions can you draw about an association between education and family size?
Answer
Solution
Following the five steps for comparing boxplots outlined in the text, we begin with the medians (step 1). These are well separated, with the median for mothers with less education being higher at an astonishing 10. The length of the box for these mothers is more than twice that of the other box (step 2). The overall spreads (distances between adjacent values) are roughly similar for the two data sets (step 3). However, this comparison is perhaps less informative about dispersion than the comparison of box lengths, because of the potential outliers in the data set for mothers with more education. The overall range for mothers with more education is rather greater if these ‘outliers’ are included. However, if the untypicality of these values were to be seen as a reason for omitting them, the range for the mothers with less education would be the greater. Whether or not they are omitted, the difference in range is not huge.
The boxplot for mothers with less education shows some slight left-skew: the left whisker is longer than the right (step 4). The main body of data for the mothers with more years of education looks symmetric, but there are three large potential outliers which would undoubtedly have an effect on any calculations of skewness (step 5).
The two batches of data seem to be distributed differently in a way which is not merely the result of difference in location. The median for the mothers with less education is close to the upper adjacent value for the mothers with more education, which leads to the conclusion that the mother's education varies with family size. The main difference between the groups lies in their different concentrations around the median rather than their overall spread of values. The potential outliers for the mothers with more education are not very far from the upper adjacent value for the other sample, and are marked as outliers essentially because of the comparatively low interquartile range for the sample into which they fall.
The overall conclusion is that the mother's education does vary with family size, with those mothers receiving six or less years of formal education having, on average, larger families.
One thing the boxplots have also shown is that three data values in one of the samples are perhaps not typical; so calculations of the mean, standard deviation and skewness should be treated with certain amount of scepticism.
1.5 Summary
In this section you have been introduced to the boxplot. This is a graphic that represents the key features of a set of data. A typical boxplot is shown in Figure 1.8.
The ends of the box mark the quartiles, and the vertical line through the box is located at the median. The whiskers of a boxplot extend to values known as adjacent values. These are the values in the data that are furthest away from the median on either side of the box, but are still within a distance of 1.5 times the interquartile range from the nearest end of the box (that is, the nearer quartile). In many cases the whiskers actually extend right out to the most extreme values in the data set. However, in other cases they do not. Any values in the data set that are more extreme than the adjacent values are plotted as separate points on the boxplot. This identifies them as potential outliers that may need further investigation.
A boxplot depicts only some basic aspects of the distribution of the values in data set. But often these basic aspects are the ones of most interest. It is straightforward to draw boxplots of more than one data set on the same scale, and then to use them to compare important aspects of the distribution of the data sets. A systematic approach to carrying out such comparisons has been described.
1.6 Exercise
Activity 3 Exercise 1.1 Memory recall times
In a study of memory recall times, a series of stimulus words was shown to a subject on a computer screen. For each word, the subject was instructed to recall either a pleasant or an unpleasant memory associated with that word. Successful recall of a memory was indicated by the subject pressing a bar on the computer keyboard. Table 1.5 shows the recall times (in seconds) for twenty pleasant and twenty unpleasant memories.
| Pleasant memory | Unpleasant memory |
|---|---|
| 1.07 | 1.45 |
| 1.17 | 1.67 |
| 1.22 | 1.90 |
| 1.42 | 2.02 |
| 1.63 | 2.32 |
| 1.98 | 2.35 |
| 2.12 | 2.43 |
| 2.32 | 2.47 |
| 2.56 | 2.57 |
| 2.70 | 3.33 |
| 2.93 | 3.87 |
| 2.97 | 4.33 |
| 3.03 | 5.35 |
| 3.15 | 5.72 |
| 3.22 | 6.48 |
| 3.42 | 6.90 |
| 4.63 | 8.68 |
| 4.70 | 9.47 |
| 5.55 | 10.00 |
| 6.17 | 10.93 |
Of key interest in this study was whether pleasant memories could be recalled more easily and quickly than unpleasant ones. Comparative boxplots for the two samples are shown in Figure 1.9.
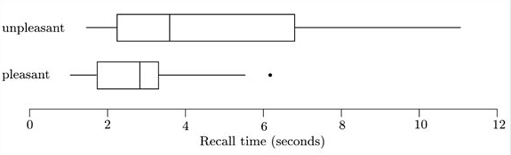
Figure 1.9
Use the boxplots to compare the distributions of recall times for the two types of memory.
Answer
Solution
The most obvious feature is that the recall times for unpleasant memories are on the whole longer than those for pleasant memories – the median, the lower quartile and the upper quartile for the ‘unpleasant’ sample are all above the corresponding values for the ‘pleasant’ sample. The dispersion is also considerably greater for the ‘unpleasant’ sample. (The interquartile range, as shown by the box lengths, is longer, and indeed so is the overall range and the lengths of the ‘whiskers’.)
Both samples are also skew. The pattern of skewness is simpler for the ‘unpleasant’ sample. It is clearly right-skew, with a long tail to the right (high values), as shown by the longer right whisker and also by the fact that the right part of the box (median to upper quartile) is longer than the left part. The ‘pleasant’ sample is not symmetric, but its pattern of skewness is a little more complicated to describe. The upper (right) whisker is longer than the lowe whisker, but the upper part of the box is shorter than the lower part.
Only one potential outlier is picked out in the boxplot – a relatively high value for the ‘pleasant’ sample. In view of the fact that it is actually not all that much higher than the upper adjacent value, perhaps this value should cause us no particular concern.
2 Producing useful tables
In much of your statistical work, you will begin with data set, often presented in the form of a table, and use the information in the table to produce diagrams and/or summary statistics that help in the interpretation of the data set. However, in practice, much interpretation of data sets can be done directly from an appropriate table of data, or by re-presenting the data in a rather different tabular form. Dealing with data in tables is the subject of this section and the next. By the time you have finished you should be able to produce tables which make certain aspects of the data in question more obvious.
2.1 Data sets in different tabular forms
Example 2.1 Lung cancer deaths in South Australia
Table 2.1 contains raw data on the incidence and mortality for lung cancer in South Australia in 1981.
| 0–4 | 47589 | 45273 | 0 | 0 | 0 | 0 |
| 5–9 | 53814 | 50672 | 0 | 0 | 0 | 0 |
| 10–14 | 58561 | 55645 | 0 | 0 | 0 | 0 |
| 15–19 | 59408 | 57756 | 0 | 0 | 0 | 0 |
| 20–24 | 58443 | 57249 | 0 | 0 | 0 | 0 |
| 25–29 | 54341 | 53376 | 0 | 0 | 1 | 0 |
| 30–34 | 53456 | 52978 | 1 | 0 | 1 | 0 |
| 35–39 | 42113 | 41988 | 0 | 2 | 0 | 0 |
| 40–44 | 35648 | 35547 | 2 | 5 | 3 | 3 |
| 45–49 | 32911 | 31799 | 8 | 2 | 10 | 2 |
| 50–54 | 36485 | 35333 | 38 | 8 | 26 | 8 |
| 55–59 | 35192 | 35555 | 61 | 18 | 43 | 8 |
| 60–64 | 28131 | 30868 | 67 | 16 | 57 | 15 |
| 65–69 | 24419 | 27390 | 88 | 15 | 69 | 17 |
| 70–74 | 16613 | 21402 | 60 | 21 | 61 | 21 |
| 75–79 | 9958 | 14546 | 46 | 10 | 46 | 9 |
| 80–84 | 4852 | 9749 | 24 | 6 | 23 | 4 |
| 85+ | 2790 | 7477 | 7 | 2 | 8 | 3 |
A table like Table 2.1 may be adequate for someone who is merely taking a quick look at the data, perhaps prior to carrying out an analysis, but it is not the best way of presenting the figures to most readers. The objectives in producing a table that is actually being used to communicate information are to make the data immediately clear, and to facilitate picking out important patterns in them with the minimum of effort. To this end, there are several guidelines for producing tables which should be borne in mind.
Guidelines for tables
Labelling of rows and columns should be clear and unambiguous.
A table should contain the minimum amount of information needed to communicate its message. This may involve splitting the data into several simpler tables or pooling cells.
It may be appropriate to simplify the numbers in a table to aid speedy comprehension.
Useful summary statistics or calculation results should be added, where appropriate, to help communicate the message.
These guidelines will be followed in relation to Table 2.1 to see what changes they suggest.
2.2 Basic table layout
As Table 2.1 stands, it is hard to assimilate the information. Indeed it is not at all clear what any of the numbers mean. Even doing something as simple as giving the columns proper headings and drawing a few lines to separate the headings from the rest of the data, as in Table 2.2, make a big difference to clarity (guideline 1).
| Age group | Population size | New cases | Deaths | |||
|---|---|---|---|---|---|---|
| Male | Female | Male | Female | Male | Female | |
| 0–4 | 47589 | 45273 | 0 | 0 | 0 | 0 |
| 5–9 | 53814 | 50672 | 0 | 0 | 0 | 0 |
| 10–14 | 58561 | 55645 | 0 | 0 | 0 | 0 |
| 15–19 | 59408 | 57756 | 0 | 0 | 0 | 0 |
| 20–24 | 58443 | 57249 | 0 | 0 | 0 | 0 |
| 25–29 | 54341 | 53376 | 0 | 0 | 1 | 0 |
| 30–34 | 53456 | 52978 | 1 | 0 | 1 | 0 |
| 35–39 | 42113 | 41988 | 0 | 2 | 0 | 0 |
| 40–44 | 35648 | 35547 | 2 | 5 | 3 | 3 |
| 45–49 | 32911 | 31799 | 8 | 2 | 10 | 2 |
| 50–54 | 36485 | 35333 | 38 | 8 | 26 | 8 |
| 55–59 | 35192 | 35555 | 61 | 18 | 43 | 8 |
| 60–64 | 28131 | 30868 | 67 | 16 | 57 | 15 |
| 65–69 | 24419 | 27390 | 88 | 15 | 69 | 17 |
| 70–74 | 16613 | 21402 | 60 | 21 | 61 | 21 |
| 75–79 | 9958 | 14546 | 46 | 10 | 46 | 9 |
| 80–84 | 4852 | 9749 | 24 | 6 | 23 | 4 |
| 85+ | 2790 | 7477 | 7 | 2 | 8 | 3 |
There is, of course, still an enormous amount of information to absorb, but the labelling is better and, above all, the table is more or less self-explanatory.
But it is important to consider what information we really want the table to convey to the reader. Here there are often choices to be made. Table 2.2 includes data on the population size in different age groups, and these data could be used to investigate the average age of the population, or the way in which the proportions of people in different age groups differ between males and females. If we wanted to convey this particular kind of information, it would make sense to simplify the table in various ways — for instance, all the data about lung cancer cases and deaths could simply be omitted! But, for this particular data set, it is much more likely that we would be interested primarily in the lung cancer cases and deaths, and in that case we would be interested in the population counts only insofar as they are related to the lung cancer counts. In that case, there is an immediate and obvious simplification to be made. There were no lung cancer cases or deaths in people aged up to 24, so we can simply pool together the first five rows of the table as in Table 2.3.
| Age group | Population size | New cases | Deaths | |||
|---|---|---|---|---|---|---|
| Male | Female | Male | Female | Male | Female | |
| 0–24 | 277815 | 266595 | 0 | 0 | 0 | 0 |
| 25–29 | 54341 | 53376 | 0 | 0 | 1 | 0 |
| 30–34 | 53456 | 52978 | 1 | 0 | 1 | 0 |
| 35–39 | 42113 | 41988 | 0 | 2 | 0 | 0 |
| 40–44 | 35648 | 35547 | 2 | 5 | 3 | 3 |
| 45–49 | 32911 | 31799 | 8 | 2 | 10 | 2 |
| 50–54 | 36485 | 35333 | 38 | 8 | 26 | 8 |
| 55–59 | 35192 | 35555 | 61 | 18 | 43 | 8 |
| 60–64 | 28131 | 30868 | 67 | 16 | 57 | 15 |
| 65–69 | 24419 | 27390 | 88 | 15 | 69 | 17 |
| 70–74 | 16613 | 21402 | 60 | 21 | 61 | 21 |
| 75–79 | 9958 | 14546 | 46 | 10 | 46 | 9 |
| 80–84 | 4852 | 9749 | 24 | 6 | 23 | 4 |
| 85+ | 2790 | 7477 | 7 | 2 | 8 | 3 |
This simplification, in line with guideline 2, has not lost any information about lung cancer at all, and the table is now easier to comprehend.
2.3 Table activity
| Age group | Population size | New cases | Deaths | |||
|---|---|---|---|---|---|---|
| Male | Female | Male | Female | Male | Female | |
| 0–39 | 427725 | 414937 | 1 | 2 | 2 | 0 |
| 40–44 | 35648 | 35547 | 2 | 5 | 3 | 3 |
| 45–49 | 32911 | 31799 | 8 | 2 | 10 | 2 |
| 50–54 | 36485 | 35333 | 38 | 8 | 26 | 8 |
| 55–59 | 35192 | 35555 | 61 | 18 | 43 | 8 |
| 60–64 | 28131 | 30868 | 67 | 16 | 57 | 15 |
| 65–69 | 24419 | 27390 | 88 | 15 | 69 | 17 |
| 70–74 | 16613 | 21402 | 60 | 21 | 61 | 21 |
| 75–79 | 9958 | 14546 | 46 | 10 | 46 | 9 |
| 80–84 | 4852 | 9749 | 24 | 6 | 23 | 4 |
| 85+ | 2790 | 7477 | 7 | 2 | 8 | 3 |
Simplifying the table further
Do you think it would make sense to continue this process of simplification by pooling more rows? If so, which rows would you pool?
Discussion
Comment
Since there were new cases, or deaths, and indeed usually both, in all the other age groups, the pooling of rows cannot be continued further without losing some information that was in the original table. But, in fact, there are very few cases in either gender group under the age of 40. So, if the corresponding rows are pooled, to give Table 2.4, very little information is lost (and, arguably, nothing at all important in relation to lung cancer). (You might have suggested a slightly different set of rows to pool.)
2.4 Including the results of useful calculation
Can Table 2.4 be simplified further by pooling more rows or columns? Perhaps it might be, but there may well be a risk of losing some important or relevant information. So, before considering any further simplification, we shall look at adding information to the table, in the form of the results of some helpful calculations (guideline 4).
On their own, some of the numbers in the table still do not mean a great deal. There were 61 new cases among males in the 55–59 age group. But how does this compare with males in other age groups, and with females? There were 60 new cases for males aged 70–74. On the face of it this looks very close to the figure for the 55–59 group. But there were far more males in the South Australian population aged 55–59 than there were aged 70–74 (35192 compared to 16613). It seems likely that the main interest in these data is in the varying chances of developing lung cancer or dying from it, at different ages and for the two genders. To find out something about this, it is useful to calculate the proportions of the different age groups that became new cases of lung cancer. For males aged 55–59, the proportion is 61/35192=0.0017333, or 0.17333% as a percentage. For males aged 70–74 the corresponding proportion is 60/16613=0.0036116, or 0.36116%. It is very common, and often very useful, to calculate such quantities, which are often known as rates.
For the time being, we shall just look at the new cases and omit the information on deaths. The rate for new cases in each age group has been calculated for males and for females; these rates are included in Table 2.5. As you can see, these numbers do not look particularly user-friendly!
| Age group | Population size | New cases | New cases as % of population size | |||
|---|---|---|---|---|---|---|
| Male | Female | Male | Female | Male | Female | |
| 0–39 | 427725 | 414937 | 1 | 2 | 0.0023380 | 0.0048200 |
| 40–44 | 35648 | 35547 | 2 | 5 | 0.056104 | 0.014066 |
| 45–49 | 32911 | 31799 | 8 | 2 | 0.024308 | 0.062895 |
| 50–54 | 36485 | 35333 | 38 | 8 | 0.10415 | 0.022642 |
| 55–59 | 35192 | 35555 | 61 | 18 | 0.17333 | 0.050626 |
| 60–64 | 28131 | 30868 | 67 | 16 | 0.23817 | 0.051834 |
| 65–69 | 24419 | 27390 | 88 | 15 | 0.36038 | 0.054765 |
| 70–74 | 16613 | 21402 | 60 | 21 | 0.36116 | 0.098122 |
| 75–79 | 9958 | 14546 | 46 | 10 | 0.46194 | 0.068747 |
| 80–84 | 4852 | 9749 | 24 | 6 | 0.49464 | 0.061545 |
| 85+ | 2790 | 7477 | 7 | 2 | 0.25090 | 0.026749 |
The table still looks pretty horrible and the information it contains is difficult to assimilate, largely because there is too much clutter from information of dubious relevance, and also because far too many decimal places are included in the last two columns. The latter problem is easily solved, in accord with guideline 3. First, note that (for example) the figure of 0.098122% for females aged 70–74 means that, for every 100 women in this age group (in South Australia in 1981), there were 0.098122 new cases of lung cancer. In this context there is nothing special about calculating the rate per 100 women in the population. Instead, the number of cases per 100 000 women in the population will be calculated. This has the effect of multiplying all the rates by 1000, which gets rid of most of the occurrences of ‘0.0…’ at the start of the numbers, and hence makes the table easier to read. Also, simply to get across the main message of these data does not require five significant figures. Instead, in Table 2.6, the figures are given to one decimal place.
| Age group | Population size | New cases | Newcases per 100 000 population | |||
|---|---|---|---|---|---|---|
| Male | Female | Male | Female | Male | Female | |
| 0–39 | 427725 | 414937 | 1 | 2 | 0.2 | 0.5 |
| 40–44 | 35648 | 35547 | 2 | 5 | 5.6 | 14.1 |
| 45–49 | 32911 | 31799 | 8 | 2 | 24.3 | 6.3 |
| 50–54 | 36485 | 35333 | 38 | 8 | 104.2 | 22.6 |
| 55–59 | 35192 | 35555 | 61 | 18 | 173.3 | 50.6 |
| 60–64 | 28131 | 30868 | 67 | 16 | 238.2 | 51.8 |
| 65–69 | 24419 | 27390 | 88 | 15 | 360.4 | 54.8 |
| 70–74 | 16613 | 21402 | 60 | 21 | 361.2 | 98.1 |
| 75–79 | 9958 | 14546 | 46 | 10 | 461.9 | 68.7 |
| 80–84 | 4852 | 9749 | 24 | 6 | 494.6 | 61.5 |
| 85+ | 2790 | 7477 | 7 | 2 | 250.9 | 26.7 |
Now does it make sense to simplify the table any further? If we want to use it to communicate information about the relative chances of being diagnosed as a new case of lung cancer at different ages and for the two genders, the ‘Population size’ and ‘New cases’ columns do not actually give very relevant information. It might therefore be reasonable to omit them. Furthermore, the general pattern of the new case rates at different ages can be communicated with rather fewer age groups than were used in Table 2.6. Table 2.7 uses fewer and coarser age groupings, and the only figures given are the calculated values of the new cases per 100 000 and deaths per 100 000; these have been rounded to one decimal place. (Note that the figures for new cases in Table 2.7 cannot be calculated simply from the rates given in the last two columns of Table 2.6. The appropriate population sizes and counts of cases must be aggregated and the aggregates used to calculate the rates.)
| Age group | New cases | Deaths | ||
|---|---|---|---|---|
| Male | Female | Male | Female | |
| 0–49 | 2.2 | 1.9 | 3.0 | 1.0 |
| 50–59 | 138.1 | 36.7 | 96.3 | 22.6 |
| 60–69 | 295.0 | 53.2 | 239.8 | 54.9 |
| 70–79 | 398.9 | 86.2 | 402.7 | 83.5 |
| 80+ | 405.7 | 46.4 | 405.7 | 40.6 |
(Whole numbers in the deaths column would arguably have been quite adequate to get across the message of these data. Using one decimal place has the advantage of making it clear that these are rates, and not counts of individual cases.)
This is a quickly assimilated table that communicates the pattern of incidence and death from lung cancer, in relation to population size. It is easy to compare the figures for males and females, and it is equally easy to compare incidence with mortality in any of the age groups.
Activity 4 Describing data in a table
(a) Describe the main patterns in the data on lung cancer in South Australia, on the basis of Table 2.7.
(b) Table 2.7 is certainly much simpler than the earlier tables in this section, and you would probably agree that the patterns in the data are easier to see. But can you think of any disadvantages of the presentation in Table 2.7 compared to the other tables?
Answer
Solution
(a) The pattern of incidence of lung cancer for males in South Australia may be described as follows. There are very few new cases in men aged under 50 years, but the rate rises rapidly for men in their 50s and 60s. The increase levels off above age 70. The pattern of mortality for males is very similar to that for incidence. For females, both incidence and mortality are again very low below 50 years of age and increase after that, but the incidence and mortality rates remain much lower than for men (about one quarter or one fifth of the level for men). Also the incidence and mortality rates for women reduce quite considerably in the oldest age groups.
(b) One problem is that the information on how many people were involved has been entirely removed. One pattern that was noted in part (a) is the fall in incidence and mortality rates for women aged over 80. However, we cannot tell from Table 2.7 that there were actually only 8 new cases and 7 deaths in women in these age groups. With numbers of cases this small, a few extra cases in one year, such as we might expect just on the basis of random variability, would show up as a large rise in the incidence rate. Without knowing something about the numbers from which the rates in Table 2.7 were calculated, it is not possible to take this into account. Thus, for example, in writing report about these matters, it would be good statistical practice to include the counts of cases and deaths somewhere, even if not in the same table as that including the rates.
Do you agree that Table 2.7 conforms to all of the four guidelines given at the beginning of this section? After you have produced a table for yourself, it is always a good idea to check it carefully against each of the four guidelines.
2.5 Early retirement from the National Health Service
Example 2.2: Early retirement from the National Health Service
A study was carried out to investigate various aspects of early retirement from the British National Health Service (NHS). In 1998–99, 5469 NHS employees from England and Wales were granted early retirement because of ill health. The researchers examined the records of a sample of 1994 of these people. Table 2.8 gives data on these people, classifying each of them by occupational group and by a broad classification of the health reason for which they retired.
| Occupational group | Reason for retiring because of ill health | ||||
|---|---|---|---|---|---|
| Musculoskeletal | Cardiovascular | Psychiatric | Other | Total | |
| Ambulance workers | 65 | 12 | 6 | 12 | 95 |
| Healthcare assistants or support | 339 | 61 | 77 | 117 | 594 |
| Nurses or midwives | 364 | 144 | 70 | 153 | 731 |
| Technical or professional staff | 42 | 25 | 4 | 23 | 94 |
| Administration or estates staff | 118 | 94 | 31 | 66 | 309 |
| Doctors or surgeons | 33 | 40 | 20 | 28 | 121 |
| Other | 22 | 13 | 7 | 8 | 50 |
| Total | 983 | 389 | 215 | 407 | 1994 |
Activity 5 Early retirement from the National Health Service
Suppose that the main interest of the researchers was to see whether (and, if so, how) the pattern of causes of retirement differed between occupational groups. How does the table, as it stands, match up to the guidelines given at the start of this section?
Answer
Solution
The labelling of rows and columns is reasonably clear as it stands (guideline 1). Assuming that the researchers were interested separately in all these occupational groups and all these reasons for retirement, there seem to be no good reasons for breaking up the table or combining cells (guideline 2). The numbers in the table are counts and not particularly large ones (three digits at most, apart from the overall total) and there seems no reason to simplify them (guideline 3).
However, it might help to include some calculation results (guideline 4). As the table stands, it is reasonably easy to see that (for instance) in each occupational group, the greatest number of retirements was due to musculoskeletal reasons, but it is not easy to compare just how much bigger that count is relative to the others in each occupational group, because the total number of retirements differs considerably from one occupational group to another. This sort of comparison would be more straightforward if we knew, for instance, the proportion or percentage of people in each occupational group who retired for musculoskeletal reasons.
Activity 6 Early retirement from the National Health Service: percentages
(a) For each occupational group, calculate the percentage of people who retired because of each cause of ill health. Use these percentages to comment on the different patterns of causes of retirement in the different occupational groups.
(b) Assuming you found the percentages useful for making these comparisons, say whether you think that a table presenting this information should include only the counts (as in Table 2.8), only the percentages that you calculated, or both.
Answer
Solution
(a) The percentage of people in each occupational group who retired because of each cause of ill health is given in Table 2.9.
| Occupational group | Reason for retiring because of ill health (% of row total) | ||||
|---|---|---|---|---|---|
| Musculoskeletal | Psychiatric | Cardiovascular | Other | ||
| Ambulance workers | 68 | 13 | 6 | 13 | |
| Healthcare assistants or support | 57 | 10 | 13 | 20 | |
| Nurses or midwives | 50 | 20 | 10 | 21 | |
| Technical or professional staff | 45 | 27 | 4 | 2 | |
| Administration or estates staff | 38 | 30 | 10 | 21 | |
| Doctors or surgeons | 27 | 33 | 17 | 23 | |
| Other | 44 | 26 | 14 | 16 | |
| Total | 49 | 20 | 11 | 20 | |
For instance, the proportion of the ambulance workers who retired because of ill health for musculoskeletal causes is 65/95=0.68421, or 68.421%. However, there is no need to include three decimal places to portray the patterns in the data clearly. Whole percentages are sufficiently accurate; so this percentage has been entered in the table as 68%. The other percentages were calculated in a similar way.
(Note that, because of the rounding of the percentages, the sums of some of the rows are 99% or 101% rather than 100%. In the context of communicating the general pattern of the data, this does not matter.)
Perhaps the most obvious difference between the occupational groups is that the percentage of retirements for musculoskeletal causes was considerably greater in the first two groups than in some of the others, particularly administrators and doctors. The authors of the paper from which these data are taken attribute this difference to the greater amount of manual work done by workers in the first two categories. The occupational groups with relatively low levels of retirement for musculoskeletal causes also had relatively high percentages of retirements for psychiatric causes. Without further investigation, and in particular without having looked at what proportion of workers in each of these groups actually retired on grounds of ill health (rather than continuing to work), it is difficult to say more about the reasons for these patterns.
(b) The question of whether to include the percentages in a table as well as, or instead of, the counts does not have a clear-cut answer. The table given in the paper from which these data were obtained includes both. This makes the table rather complicated, and the patterns of different causes of retirement is not entirely clear at a glance. However, in interpreting the data it is important to know that the number of ill-health retirements in some of these groups was not particularly large. A useful compromise would have been to include the total number of retirements from which the percentages in each row were calculated, as in Table 2.10. In general, when calculating row percentages (or column percentages) in a table in this way, it is good practice to include the totals that were used to calculate the percentages as well.
| Occupational group | Reason for retiring because of ill health (%of row total) | ||||
|---|---|---|---|---|---|
| Musculoskeletal | Psychiatric | Cardiovascular | Other | Total (=100%) | |
| Ambulance workers | 68 | 13 | 6 | 13 | 95 |
| Healthcare assistants or support | 57 | 10 | 13 | 20 | 594 |
| Nurses or midwives | 50 | 20 | 10 | 21 | 731 |
| Technical or professional staff | 45 | 27 | 4 | 24 | 9 |
| Administration or estates staff | 38 | 30 | 10 | 21 | 309 |
| Doctors or surgeons | 27 | 33 | 17 | 23 | 121 |
| Other | 44 | 26 | 14 | 16 | 50 |
| Total | 49 | 20 | 11 | 20 | 1994 |
2.6 Summary
In this section you have been introduced to some guidelines for presenting data in tables. These guidelines apply particularly when the data in a table are being used to illustrate a particular point or to show up clearly a particular pattern.
You have seen that, in some circumstances, following the second of these guidelines leads to some pooling together of rows. (In other cases, it could be columns or individual cells that are pooled.) However, care is needed when, by making such simplifications, information is lost from the table. The examples of the application of guideline 4 that you have seen involve calculating appropriate ratios or rates. Such calculations are very common in dealing with data in tabular form.
3 Interpreting data in table
In Section 2, the main concern was with producing a table of data, for others to read, that communicates clearly the important patterns or messages in the data. In this section, the focus changes slightly. Your role will be that of the reader or user of the data in a table, and you will learn about approaches that make it easier for you to extract information from a table. However, manipulating tabular data into a form that makes it clearer to others will also, very often, make it clearer to you as well. So the approaches introduced in Section 2 will be useful in this section too. You will have more practice in choosing and calculating appropriate ratios and rates for tabular data. You will also see examples where it is appropriate to go one step further than you did in Section 2: rather than leaving the data in tabular form, relevant graphs will be drawn as well.
3.1 Health personnel in Thailand
There are practically no new theories or new principles in this section. We shall work through some examples, and you will see how basic techniques and approaches that you have already learned can be combined to allow you to use tabular data efficiently.
Example 3.1 Health personnel in Thailand
The data shown in Table 3.1 are taken from the Thailand Mini Health Profile 1988, published by the Ministry of Public Health, Bangkok. They show the numbers of health care personnel at approximately five-year intervals.
| Category | 1966 | 1971 | 1976 | 1981 | 1984 |
|---|---|---|---|---|---|
| Physicians | 3609 | 4092 | 5210 | 6931 | 8058 |
| Dentists | 253 | 532 | 600 | 1057 | 1326 |
| Pharmacists | 940 | 1586 | 1757 | 2680 | 3312 |
| Nurses | 6876 | 9760 | 13700 | 19599 | 31827 |
| Midwives | 2834 | 4989 | 7304 | 8577 | 8573 |
| Total | 14512 | 20959 | 28571 | 38844 | 53096 |
What do these data tell us about the change in health care personnel in Thailand over the period in question, and how can we work with the data in the table to make any pattern clearer?
First, notice that some features of the data are obvious. The total number of health care personnel increased hugely between 1966 and 1984, from under 15 000 to about 53 000. Also, throughout the period, the biggest category of staff was that of Nurses, and this category seems to have grown more rapidly than some of the others. (In 1966, there were very roughly twice as many nurses as there were doctors, for instance, but in 1984 there were almost four times as many nurses as there were doctors.)
How could the patterns that have already been identified be made clearer? The pattern of overall increase in numbers is already clear from the last row of the table. Perhaps it could be made even clearer by drawing an appropriate graph; we shall return to this idea later.
In Activity 6, the patterns of retirement reasons in different occupational groups were made easier to see by calculating how large each entry was as a percentage of the corresponding row total. In Activity 7, you are asked to consider whether similar approach would help here.
3.2 Health care personnel in Thailand: activities
Activity 7 Health care personnel in Thailand: calculating percentages
Would it be helpful, in considering possible changes in the way health care personnel are divided into the five categories listed, to recalculate the numbers in the body of Table 3.1 as percentages either of the row totals or of the column totals? If you think it would be helpful, calculate the appropriate percentages and use the resulting table to comment on the data.
Answer
Recalculating the numbers in the body of the table as percentages of the totals of the columns would show clearly how the total number of health personnel in each year is divided between the five categories. It would not be very meaningful to calculate the percentages of the row totals. The results of calculating the numbers as percentages of the column totals are shown in Table 3.2.
| Category | 1966 | 1971 | 1976 | 1981 | 1984 |
|---|---|---|---|---|---|
| Physicians | 25 | 20 | 18 | 18 | 15 |
| Dentists | 2 | 3 | 2 | 3 | 2 |
| Pharmacists | 6 | 8 | 6 | 7 | 6 |
| Nurses | 47 | 47 | 48 | 50 | 60 |
| Midwives | 20 | 24 | 26 | 22 | 16 |
| Total (= 100%) | 14512 | 20959 | 28571 | 38844 | 53096 |
These percentages show that the numbers for dentists and for pharmacists as percentages of the total health care personnel changed very little over the period covered by the table. However, the percentage of physicians fell reasonably steadily from 25% of the total in 1966 to 15% in 1984. The percentage of nurses grew slowly from 1966 to 1981, but then increased rapidly between 1981 and 1984. Finally, the percentage of midwives increased over the first ten years of the period covered, but then fell back to a level below the 1966 level. Of course, it should be borne in mind throughout that the total number of health care staff grew considerably over the period.
Your investigation in Activity 7 clarified the patterns in the original table; but it remains the case that the single most prominent feature of the table is the rise in total health care personnel over the period covered. However, it may well have occurred to you that the population served by these health care personnel also changed over the period in question. Thailand is, after all, a developing country that may well have experienced considerable population growth between 1966 and 1984.
In fact, estimates of the total population of Thailand in the years covered by Table 3.1 are also provided in the source from which that table was taken. They are given in Table 3.3.
| 1966 | 1971 | 1976 | 1981 | 1984 | |
|---|---|---|---|---|---|
| Population (millions) | 31.1 | 35.4 | 40.3 | 44.9 | 50.7 |
These figures can be used to calculate the numbers of the different categories of health care personnel as a proportion of the total population. These proportions could, in principle at any rate, be shown as percentages, or as numbers per 100 000 population as in Example 2.1 (see especially Tables 2.6 and 2.7); but in this case they are clearer if shown as numbers per million population. The resulting proportions are given in Table 3.4. After reading through the table you should check that you understand how the numbers displayed were calculated.
| Category | 1966 | 1971 | 1976 | 1981 | 1984 |
|---|---|---|---|---|---|
| Physicians | 116.0 | 115.6 | 129.3 | 154.4 | 158.9 |
| Dentists | 8.1 | 15.0 | 14.9 | 23.5 | 26.2 |
| Pharmacists | 30.2 | 44.8 | 43.6 | 59.7 | 65.3 |
| Nurses | 221.1 | 275.7 | 340.0 | 436.5 | 627.8 |
| Midwives | 91.1 | 140.9 | 181.2 | 191.0 | 169.1 |
| Total | 466.6 | 592.1 | 709.0 | 865.1 | 1047.3 |
These calculations show clearly that, in relation to the size of the total population, the total numbers of health care personnel in Thailand rose considerably and steadily between 1966 and 1984. Putting it another way, the population rose over this period, but the numbers of health care personnel rose much faster. It would be reasonably straightforward to comment on the changes in the different categories in relation to total population on the basis of the numbers in Table 3.4, but this task can be made easier by drawing an appropriate graph.
Data like those in Table 3.4, where there is a value for each of a number of different times, are referred to as time series. (In this case, there are actually six different time series, one for each personnel category, plus one for the data on total health personnel.) A useful kind of graph for showing time series data is line plot. This is a scatterplot, with the times (years, in this case) along the horizontal axis and the actual data values of the time series along the vertical axis. It is conventional, for time series data, to join the resulting plots with straight line segments. This draws attention to the rate of change of the values in the series. For time series where there are large numbers of different time points, the symbols (for example, crosses or dots) representing the data points are often omitted for clarity. However, in these data there are only five time points so it is not necessary to do that. We could produce such line plots separately for each of the different categories, and indeed for the total. But it is often easier to compare the levels of different time series by plotting them all on the same graph. Figure 3.1 shows such a graph, with a set of points and a line for each of the categories. (The series for total personnel is omitted. Since the totals are necessarily bigger than the figures for the individual groups, including them on the same graph would squeeze up all the other lines towards the bottom of the diagram and make them hard to see.)
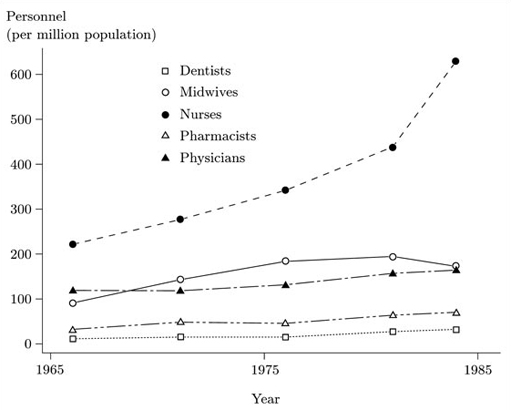
Figure 3.1
Activity 8 Health care personnel: interpreting line graphs
Comment on the main changes in health care personnel per million population in Thailand over the period 1966–1984, on the basis of Figure 3.1. Are there any important patterns in the data in Table 3.4 that the graph does not make clear?
Answer
It is clear from Figure 3.1 that the numbers for personnel in each category, in relation to the total population of the country, rose quite markedly over the period in question. The rise was very marked for nurses (who were the largest category throughout the period), particularly towards the end of the period covered, between 1981 and 1984. There are some exceptions to this overall pattern of increase, the most prominent of which is that the number of midwives per million population actually fell by considerable amount between 1981 and 1984.
It is very clear from the graph that the numbers for dentists and for pharmacists per million population are considerably less than the corresponding numbers for the other categories; and it is reasonably clear that the numbers for both these groups rose over the period. However, because the numbers for these groups are so much smaller than, say, the numbers for nurses, the lines for dentists and for pharmacists are rather squashed up at the bottom of the graph and it is therefore difficult to judge the size of the increase. It is thus much clearer from the table than from the graph that the number of dentists has more than tripled in relation to the population size over the period, and that the number of pharmacists has more than doubled. It is also not very clear from the graph that the numbers for dentists and for pharmacists fell slightly in relation to the population between 1971 and 1976.
Activity 9 Health care personnel: more on proportions
Your work in Activity 7, on the proportions of health care personnel in the different categories, did not take account of the total population of Thailand. Explain why, if you calculated the figures in Table 3.4 as percentages of the column totals, you would get exactly the same table of percentages as that in the solution to Activity 7. If you wanted to represent these percentages graphically, what kind of graph would you draw?
Answer
The figures in any particular column of Table 3.4, including the column totals, are equal to the figures in the corresponding column of Table 3.1 divided by the population estimate from the corresponding column of Table 3.3. Thus in carrying out a division to calculate a percentage from Table 3.4, the quantities in the numerator and in the denominator were calculated from Table 3.1 by dividing by the same population total. So the population total cancels out and the result of the division is identical to that obtained from Table 3.1.
One appropriate kind of graph that would draw particular attention to the proportions is the pie chart. We could draw separate pie charts for each of the years listed in the table. The appropriate pie charts for the 1966 and 1984 data are shown in Figures 3.2 and 3.3 respectively. (You were not asked to draw these in the activity!)
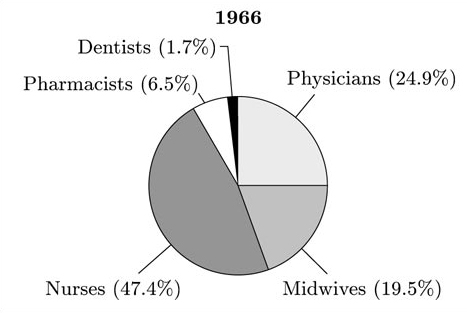
Figure 3.2
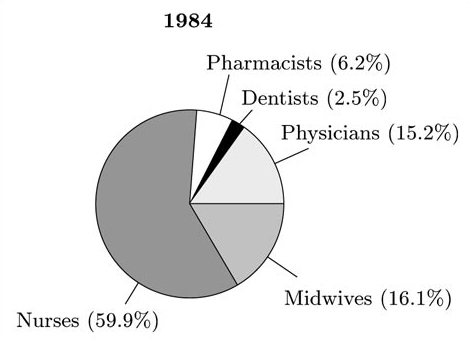
Figure 3.3
These pie charts draw particular attention to the large increase in the number of nurses as a proportion of total health care personnel in Thailand between 1966 and 1984.
In Example 3.1, the original data were counts of individuals. It proved useful to calculate appropriate percentages, by dividing the numbers in the body of the table by column totals. In Activity 2.4, you calculated similar percentages, but they were based on row totals. In Example 3.1, it would have made very little sense to calculate percentages of the row totals. However, in Activity 6, it would have made sense to calculate the percentages of column totals instead of row totals, but they would have provided information relevant to a different question from the one you were considering. For tables of counts in general, it is very often useful to calculate percentages of row totals, and/or of column totals, but it is important to think carefully about which set of percentages is informative in relation to the question you are interested in. The following example is intended to make this clear.
3.3 HIV testing in sub-Saharan Africa
Example 3.2 HIV testing in sub-Saharan Africa
In developed countries, the standard method for testing whether a person is infected with the virus HIV, that causes AIDS, is to carry out a blood test. Provided such a test is carried out long enough after the initial infection occurred, the accuracy is high. However, in sub-Saharan Africa, where in most countries the incidence of AIDS is much higher than in the developed world, blood testing can be difficult to conduct and it is expensive in terms of the health resources available. Thus there is interest in whether HIV infection can be diagnosed at all reliably on the basis of clinical features that are more easily measured or observed under the local circumstances. People infected with HIV often have enlarged lymph nodes, and these enlarged nodes can be felt from the outside of the body in a simple physical examination. However, there are very many other reasons as well as HIV infection for an individual to have enlarged lymph nodes. (In countries like the UK, the overwhelming majority of enlarged lymph nodes are caused by infections that have nothing whatever to do with HIV or AIDS.)
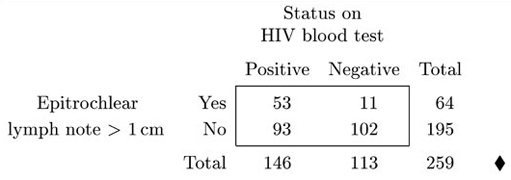
To investigate whether enlarged lymph nodes could play a role in testing for HIV in an African context, researchers in Zimbabwe investigated all adult patients admitted to an acute medical ward in a Harare hospital over a three-month period (apart from one patient who did not agree to take part). Each patient was tested for HIV using a standard (and an accurate) blood-testing method. (In fact, 56% of the patients turned out to have an HIV infection according to these tests.) In addition, the patients were examined (by feeling) for enlarged lymph nodes in three areas of their body. The data in Table 3.4 provide information on the numbers of patients who had an epitrochlear lymph node (a node in the upper arm near the elbow) swollen to a size larger than 1 cm.
Activity 10 HIV testing: calculating proportions
(a) Suppose you were a doctor practising in a hospital in sub-Saharan Africa, in a place where the general characteristics of patients that you see is likely to be reasonably similar to those reported on in Table 3.4. You decide to investigate for enlarged epitrochlear lymph nodes in the patients you see and, depending on whether you find such a node enlarged to over 1 cm, to use this information together with that in Table 3.4 to take a view on how likely it is that the patient has HIV. Would it help you more to recalculate the numbers in the main body of Table 3.4 as percentages of the row totals or the column totals? Calculate the set of percentages you believe to be more appropriate. In the light of your results, what would be your view on how likely it is that patient with an epitrochlear node over 1 cm actually has HIV (according to blood test). What about a patient who does not have such a node?
(b) Suppose now that you are a scientific researcher interested in the physiological mechanism by which HIV infection can cause enlarged lymph nodes. In investigating this topic, would it help you more to recalculate the numbers in the main body of Table 3.4 as percentages of the row totals or the column totals? Calculate the set of percentages you believe to be more appropriate and comment on what you find.
Answer
(a) In this situation, suppose one of your patients has an epitrochlear lymph node enlarged to more than 1 cm. You might then want to ask ‘What proportion of such patients actually have HIV (as would show up if they were given a standard blood test)?’ That is, you know your patient corresponds to those in the first row of Table 3.4. If your patients are generally comparable to those in the Harare hospital, the proportion can be estimated by calculating the number in the first row of Table 3.4 as a percentage of the row total. For this reason, calculating the figures in the table as percentages of the row totals is helpful, and the percentages of the column totals are less relevant. Calculating all the figures as percentages of the row totals leads to Table 3.5. (The percentages have been rounded to whole numbers.)

Table 3.5: Percentages of row totals for Harare hospital patients
This table shows that 83% of the patients who had an enlarged epitrochlear lymph node of size over 1cm were actually infected with HIV (according to the blood test). In this context, it is quite likely that a patient with such an enlarged node will have HIV. (But bear in mind that these figures will not apply in other contexts. As Table 3.5 again makes clear (in the bottom line), 56% of all the patients in the study were HIV positive on the blood test. In a hospital in, say, Europe, this will not be the case, and it is much more likely that an enlarged epitrochlear lymph node would have some other explanation.)
The table also shows that 52% of the patients who do not have an enlarged epitrochlear lymph node of this size were not HIV positive. In the Harare context, not having this particular physical sign does not actually say much about the patient's chances of being free from HIV. The chance is rather more than would be the case for patients in general, but not much more.
(b) In this case the scientist will probably be more interested to ask ‘Of the patients who actually are HIV positive on the blood test, what proportion show an enlarged epitrochlear lymph node of this size?’. That is, the scientist would be interested in knowing how large the numbers in the table were in relation to the column totals rather than the row totals. The resulting percentages are shown in Table 3.6.
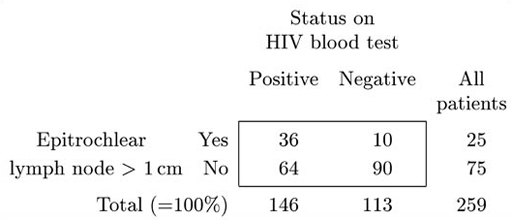
Table 3.6
This table shows that, of the Harare patients who are HIV positive (on the blood test), 36% have this type of enlarged lymph node (so most of them do not have it). However, the fact that the presence of an enlarged lymph node of this type does have some diagnostic value is shown by the fact that a much smaller proportion, just 10%, of HIV negative patients show this particular sign.
It is worth noting that the percentages in Table 3.5 are considerably different from those in Table 3.6. Thus if you were interested in the scientist's question but calculated, mistakenly, the percentages relevant to the doctor (that is, the row percentages), you could be seriously misled.
For the data in Table 3.4, both the row percentages and the column percentages turned out to be useful quantities to calculate; but which is more useful depends on the question you are trying to answer. It is crucial not to use the row percentages to answer questions that relate to the column percentages, or vice versa. As you saw in Activity 10, the two sets of percentages can be considerably different. In general, in making calculations from data in tables, it is always important to think through carefully exactly what you want to know.
Before the final activity, some threads relating to graphics will be drawn together. You have now met several different graphics: pie charts, bar charts, histograms, scatterplots, boxplots and line plots of time series. You have seen that different types of plot are suitable for different types of data. You have also seen that the choice of an appropriate graph for presenting and examining data can depend on the question of interest. The following guidelines draw together what you have learned so far.
3.4 Guidelines for graphics
Data in the form of counts of individual entities (for example, people, animals, power stations) in a small set of discrete categories can be presented in bar charts or pie charts. For most purposes, bar charts are preferable. Pie charts draw particular attention to the proportions in which the entities are split between the different categories. However, they do so by representing the proportions by angles, and even when the main interest lies in the proportions, bar charts may well be easier to ‘read’.
For data in the form of category counts where the interest lies in comparing two or more data sets (as in Example 2.3 of Unit A1 ), it can be useful to produce a bar chart where the corresponding bars for the different data sets are plotted side by side.
To examine the pattern of distribution of values of a continuous (measured) variable, a histogram is an appropriate graphic. An alternative is a boxplot. However, neither sort of plot gives direct information about the number of observations in the data set, and it can be risky to draw firm conclusions about the pattern of distribution when the number of observations is small.
Boxplots give a simple representation of the values of a continuous variable. They can also be used for discrete variables where the categories are numbers (such as the counts of family sizes in Figure 1.7. A boxplot shows less detail about a distribution than an appropriate histogram or bar chart, but the amount of detail in a boxplot is often sufficient.
Boxplots are particularly useful for comparing two or more data sets, because the corresponding boxplots can be drawn against a common scale on the same diagram. (It is difficult to do this clearly with more than one histogram.)
Scatterplots are used when the values of two numerical variables have been obtained from each of a number of individual entities. The aim of the plot is to investigate the relationship between the values of the two variables.
Line plots can be useful, particularly for time series data, because they draw attention to the way that one or more variables have changed over time.
In some circumstances, particularly when the data are very skew, more informative boxplot or scatterplot can be produced by transforming the data first.
This section ends with a more substantial activity. This will provide you with some further experience of dealing with data in tables. You will also be asked to look at one or two slightly different approaches for interpreting tabular data.
3.5 The British Crime Survey
| 1997 Police | 1997 BCS | % BCS reported | % recorded of reported | % recorded of all BCS | % change 1995 to 1997 | % change 1981 to 1997 | |||
|---|---|---|---|---|---|---|---|---|---|
| Police | BCS | Police | BCS | ||||||
| Vandalism | 443 | 2917 | 26 | 58 | 15 | −4 | −15 | 121 | 7 |
| All comparable property theft (acquisitive crime) | 1751 | 6261 | 50 | 56 | 28 | −17 | −15 | 51 | 99 |
| Burglary | 519 | 1639 | 64 | 49 | 32 | −19 | −7 | 48 | 119 |
| Attempts & no loss | 140 | 976 | 50 | 29 | 14 | −17 | −0.1 | 90 | 160 |
| With loss | 379 | 664 | 85 | 67 | 57 | −20 | −15 | 37 | 77 |
| All vehicle thefts | 1022 | 3483 | 47 | 62 | 29 | −15 | −19 | 57 | 99 |
| Theft from vehicle | 552 | 2164 | 43 | 59 | 25 | −16 | −14 | 63 | 68 |
| Theft of vehicle | 316 | 375 | 97 | 87 | 84 | −21 | −25 | 10 | 31 |
| Attempted thefts | 154 | 943 | 37 | 44 | 16 | 3 | −27 | 447 | 425 |
| Bicycle theft | 151 | 549 | 64 | 43 | 27 | −18 | −17 | 19 | 154 |
| Theft from the person | 60 | 590 | 35 | 29 | 10 | −4 | −12 | 71 | 36 |
| All comparable violence | 256 | 1022 | 49 | 51 | 25 | 11 | −13 | 150 | 53 |
| Wounding | 205 | 714 | 45 | 63 | 29 | 18 | −17 | 143 | 41 |
| Robbery | 52 | 307 | 57 | 30 | 17 | −11 | −2 | 183 | 89 |
| All comparable | 2450 | 10199 | 44 | 54 | 24 | −12 | −15 | 67 | 56 |
Activity 11 The British Crime Survey
The British Crime Survey (BCS) is a sample survey carried out in England and Wales by the Home Office. The survey was first carried out in 1982, and at the time of writing (2001) is done every two years. The aim is to measure the level of crimes against people in private households. Data are collected by interviewing adult respondents from a representative sample of households about their experience as victims of crime in the previous year, and about some other matters connected with crime. For the 1998 BCS, a respondent from each of approximately 15 000 households was interviewed.
Apart from the BCS, the main source of data on crime in England and Wales is police records. Data on crimes from police records are not entirely comparable with those from the BCS, mainly because certain categories of crime are not covered by both sources of data. (For instance, frauds against companies are not recorded in the BCS because there is no personal victim in a private household.) However, there is a large set of categories of crime for which BCS data and police records should (in principle at least) be comparable. Table 3.5 is taken from the report on the 1998 BCS (and hence relates to crimes in 1997), and it compares in various ways the numbers (in thousands) of crimes (in these comparable categories) recorded by the police and measured by the BCS. (The BCS figures are estimates, based on the sample data, for total numbers of crimes in these categories in England and Wales.) In the BCS, respondents are asked, in relation to any crime of which they were a victim, whether or not it was reported to the police. Many crimes are not reported to the police, and clearly these crimes will not appear in the police records.
Some of this activity is concerned with making sense of where the figures come from in this rather complex table. In fact, rather more clues about the relationships between the different numbers are contained in the text of the report. However, with other reports and other tables, this is regrettably not always the case, so the practice you will get by working through this activity will be worthwhile!
Note also that the questions below ask you to answer briefly. Being able to make statistical points concisely in writing is an important skill generally (as well as being crucial in an examination context where time is limited).
(a) The row labelled ‘All comparable’ at the bottom of Table 3.5 concerns values for all offences in the comparable categories taken together. Explain briefly how the first three percentages in that row (44, 54, 24) relate to one another and to the first two values (2450, 10199) in the row.
(b) Consider the column labelled ‘1997 Police’. Describe briefly how values in this column are related to one another.
(c) Draw a suitable diagram to display the values associated with ‘Vandalism’, ‘Burglary’, ‘All vehicle thefts’, ‘Bicycle theft’, ‘Theft from the person’ and ‘All comparable violence’, using the values in the ‘1997 BCS’ column.
(d) Find and use the appropriate numbers from the table to calculate the equivalent values in 1981 to those in part (c). Draw a diagram to display these values. Using your diagrams and/or the corresponding numbers, comment briefly on the similarities and differences between the numbers of crimes in these categories in 1981 and 1997.
Answer
The questions in this activity generally required you to answer briefly. This solution is not particularly brief, because it contains material intended to explain to you what is going on. However, to clarify matters, this explanatory material is enclosed in square brackets.
(a) The value 44 [in the ‘% BCS reported’ column] is the percentage of the crimes mentioned in the BCS that, according to the BCS respondents, were reported to the police. It cannot be calculated from other values in the table. However, it can be used to deduce that the number of ‘comparable’ crimes that were reported to the police, according to BCS respondents, was 44% of 10 199 thousand, or 4488 thousand [to the nearest thousand].
The value 54 [in the ‘% recorded of reported’ column] is the percentage of the crimes that BCS respondents said were reported to the police that actually appear in the police crime statistics. It has already been calculated that 4488 thousand crimes in these categories were said by BCS respondents to have been reported to the police. According to police records, 2450 thousand such crimes were reported to them. Thus the figure of 54% is calculated as the ratio 24504488 [and indeed, allowing for some rounding error, the figures do match].
Finally, the value 24 [in the ‘% recorded of all BCS’ column] is the ratio of the total number of crimes reported to the police (according to police records) to the number of crimes recorded in the BCS. That is, it is 2450/10 199 [and again this does come to 24%].
(b) [In the ‘1997 Police’ column and, indeed, in the ‘1997 BCS’ column, the total number of comparable crimes is divided between various different categories, and some of the categories are further divided in subcategories, and in some cases these are further divided.] The value 2450 for ‘All comparable’ is the sum of the values for the categories shown in bold type, namely ‘Vandalism’, ‘All comparable property theft’ and ‘All comparable violence’. The value for ‘All comparable violence’ is approximately the sum of the values for ‘Wounding’ and ‘Robbery’. [Actually that sum is 257, not 256, but that is presumably accounted for by rounding errors, given that these values are all rounded to the nearest thousand crimes.] The value 1751 for ‘All comparable property theft’ is, within rounding error, the sum of the values for ‘Burglary’, ‘All vehicle thefts’, ‘Bicycle theft’ and ‘Theft from the person’. Finally, the values for ‘Burglary’ and for ‘All vehicle thefts’ are the sums of the values in the relevant rows given below each of these headings.
(c) [These are data in the form of counts of individual entities, in this case crimes, in a number of discrete categories. Guideline 1 for graphics suggests that there are two appropriate types of plot – a bar chart or a pie chart. Both are given here, although only one is required to answer the question. Perhaps the more appropriate is a bar chart, where the lengths of the bars indicate the numbers of crimes in each of the categories. A bar chart for the numbers of crimes in the named categories is shown in Figure 3.4.
Alternatively, you may have felt that the most important point here was the way that the total number of comparable crimes was divided between these categories, in which case a pie chart might be more appropriate. However, the pie chart does not show directly the total number of crimes involved, so that a bar chart is arguably the better choice. A pie chart for the data is shown in Figure 3.5.]
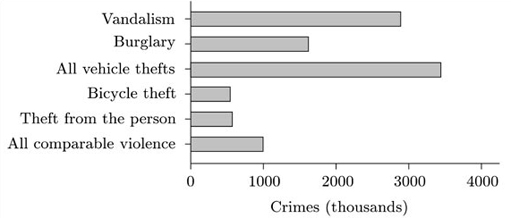
Figure 3.4
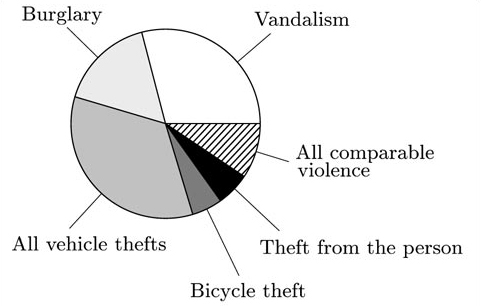
Figure 3.5
(d) [Here, the relevant numbers in the table are those in the ‘1997 BCS’ column, and those in the ‘% change 1981 to 1997: BCS’ column. For the ‘Vandalism’ category, there were 2917 thousand crimes (BCS) in 1997, and the final column of the table indicates that this value is 7% higher than that for 1981. Thus the 1981 value for ‘Vandalism’ can be calculated as follows:
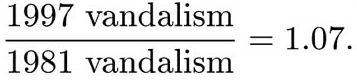
So

in thousands, to the nearest thousand. The other figures can be calculated in similar manner and are given below, all rounded to the nearest thousand.]
| Vandalism | [2 917/1.07=] 2726 |
| Burglary | [1639/2.19=] 748 |
| All vehicle thefts | [3 483/1.99=] 1750 |
| Bicycle theft | [549/2.54 =] 216 |
| Theft from the person | [590/1.36 =] 434 |
| All comparable violence | [1022/1.53=] 668 |
[A bar chart for these data is shown in Figure 3.6 and a pie chart in Figure 3.7. Only one of these charts is required to answer the question.]

Figure 3.6
Figure 3.7
[In fact, a better way of portraying these data, instead of either Figure 3.6 or Figure 3.7, for the purpose of the comparison you are asked to make is to plot both the 1981 and the 1997 figures on the same bar chart (guideline 2), as in Figure 3.8.]
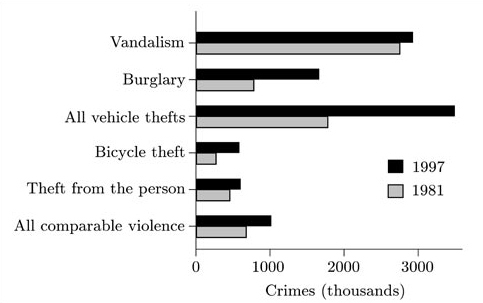
Figure 3.8
[Whichever diagram you drew, the following should be reasonably clear.] The pattern of crimes in these different categories changed considerably between 1981 and 1997. In 1981 vandalism was, by a large margin, the most common category, though the number of vehicle thefts was also large. By 1997, the numbers of crimes in all categories had increased, though the increase in the number of crimes of vandalism was relatively small. However, there had been very large increases in numbers of vehicle thefts, of bicycle thefts and of burglaries, and vehicle thefts had become the largest category. The two smallest categories in 1981 were thefts from the person and bicycle thefts, and this remained the case in 1997 even though the number of bicycle thefts had increased by over 150%.
3.6 Summary of Section 3
In this section, you have learned about appropriate ways of interpreting data in tables. By working through examples, you have seen how it can be useful to calculate appropriate proportions and ratios, and to present some of the data in graphical form. Guidelines for the choice of graphics have been given. When the data in a table are in the form of counts, you have seen that it can be useful to calculate the counts in a particular row or column as proportions (usually in the form of percentages) of the corresponding row or column total. However, it is important to calculate the proportion that is relevant to the question you are trying to answer.
4 Conclusion
In this course, you have learned about boxplots and about ways of dealing with data given in tabular form.
A boxplot is a way of presenting certain summary statistics and other characteristics of a data set in graphical form. It gives a quick graphical impression of the location, dispersion and the general pattern of skewness in data set, as well as drawing attention to unusually large or small values. In comparing two or more data sets, it is often useful to draw comparative boxplots (that is, draw boxplots for the data sets on the same diagram against the same scale). These can be used to compare the data sets in terms of location, dispersion and symmetry or skewness. For some data sets that exhibit considerable skewness, this process of comparison is sometimes made easier by transforming the data first.
You have seen how the presentation of data in tabular form can often be improve by following certain guidelines. The labelling of the rows and columns in a table should be clear; unnecessary information should not be included; it may be useful to simplify the numbers in the table (for example, by reducing the number of significant figures presented); and summary statistics or calculation results can often usefully be added to table.
When you are faced with the task of interpreting data in a table, it is very often useful to calculate appropriate rates or proportions to clarify the message of the table. Patterns in the data may also become clearer if an appropriate graph is drawn. Guidelines on the choice of graph have been given. You have seen that it is important to understand how the different numbers in a table relate to one another.
Don't miss out:
1. Join over 200,000 students, currently studying with The Open University http://www.open.ac.uk/ choose/ ou/ open-content
2. Enjoyed this? Find out more about this topic or browse all our free course materials on OpenLearn http://www.open.edu/ openlearn/
3. Outside the UK? We have students in over a hundred countries studying online qualifications http://www.openuniversity.edu/ including an MBA at our triple accredited Business School.
Acknowledgements
Except for third party materials and otherwise stated (see terms and conditions), this content is made available under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Licence
Course image: Paul L Dineen in Flickr made available under Creative Commons Attribution 2.0 Licence.
Don't miss out:
If reading this text has inspired you to learn more, you may be interested in joining the millions of people who discover our free learning resources and qualifications by visiting The Open University - www.open.edu/ openlearn/ free-courses
Copyright © 2016 The Open University