Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
An introduction to electronics
An introduction to electronics

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

4.5 Making signals from combinations of sine waves

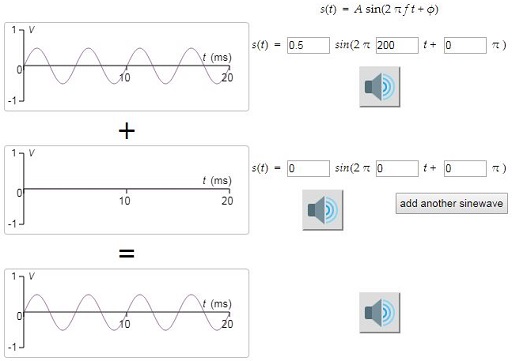
Right-click on the image below to open Interactive 3 in a new tab, then change the values for the top two waves so that the frequency of the first is 440 Hz and the frequency of the second is 660 Hz. Make the amplitude of both 0.5.

The wave at the bottom is formed by combining these two waves, by adding their values for each value of t.

Click on the loudspeaker button for each of the top two waves and listen to the resulting sounds. Then click on the loudspeaker button for the bottom wave and listen to its sound.


View interactive version
Interactive 3 Combining sine waves
Show description|Hide description

This is an interactive that may be used to add two or more sine waves together, display a visual representation of the result and also hear its sound. To start with, three graphs are shown in a vertical column on the left. Each one displays voltage between minus 1 and 1 volts against time between 0 and 20 milliseconds. Beside each of the three graphs is a loudspeaker button. To the right of each of the top two graphs is its corresponding sine wave equation, with type-in text boxes to change the amplitude, frequency and period. Finally, an ‘add another harmonic’ button is positioned to the right of the loudspeaker button belonging to the second graph.

When values are input to the sine wave equations beside the top two graphs, a visual representation of the sine wave is shown on the graph and you can also listen to it by clicking on the loudspeaker button. In addition, the result of adding the two sine waves is shown on the bottom graph and this can also be listened to by clicking on the corresponding loudspeaker button. Clicking on the ‘add another harmonic’ button inserts another graph with sine wave parameters above the bottom graph, allowing you to sum three sine waves instead of two, and so on.

This interactive changes according to the parameters you enter and therefore you may need a sighted helper to describe the waveforms to you.

Interactive 3 Combining sine waves
Interactive feature not available in single page view (see it in standard view).

SAQ 8

  • a.Is the composite signal at the bottom a sine wave?
  • b.What is the ratio of the frequencies of the sine waves at the top?
  • c.Does the combined signal sound pleasant with the single sine waves in harmony?
  • d.Do you think there is any relationship between the ratio of the frequencies and the notes harmonising?

Answer

  • a.No, the combined signal is not a sine wave. It has a more complicated shape.
  • b.The ratio of the frequencies is 440:660 or 2:3.
  • c.This is a subjective question, but you may agree that it sounds as if the individual waves do combine to make a harmonised sound.
  • d.Generally, in music, notes with frequencies in simple proportions harmonise with each other.

SAQ 9

Keep the frequency of the first wave at 440 Hz and its amplitude at 0.5. Change the frequency of the second wave to 880 Hz and change its amplitude to −0.17 (don’t overlook the minus). What is the shape of the resulting wave?

Answer

The resulting wave has a triangular shape, as shown in Figure 25. This could be called a ‘sawtooth’ wave.

Described image
Figure 25 Sawtooth wave
Show description|Hide description

This is a screenshot from Interactive 3, showing just the bottom wave. As usual, the horizontal axis shows time from 0 to 20 milliseconds and the vertical axis shows voltage from minus 1 to 1 volt. The wave looks like a zig-zag that starts at 0, rises diagonally up to a maximum of approximately 0.6 volts and then falls diagonally down to a minimum of approximately minus 0.6 volts, before rising diagonally back up to 0 and repeating. This cycle occurs just under 9 times. The diagonal lines have a slight ‘wobble’ to them, but this is a reasonable approximation to a sawtooth wave.

Figure 25 Sawtooth wave

Keep the interactive open, because you will need it in the next section.