1.6.2 Crystal lattices and unit cells

A typical crystal contains billions of atoms in a highly ordered structural arrangement. Perhaps surprisingly, the essence of such a complex structure can be described relatively simply. How is this possible?

If you tried to tile a two-dimensional area such as a bathroom floor without any gaps, you would do this by adding tiles that fitted together. In fact, only tiles with two-, three- four- and six-fold symmetry allow for successful tiling (Figure 22). Similarly, if you tried to produce a three-dimensional structure (like a crystal) without any gaps it would require the repetition of building blocks (i.e. 3D repeating units) with particular shapes. As with two-dimensional tiling, the only kinds of rotational symmetry axis possible in three-dimensional crystals are two-, three-, four- and six-fold axes.

Figure 22 Two-dimensional tiling. Some shapes cannot be tiled without gaps appearing. Only two-, three-, four- and six-fold symmetry are consistent with periodic repetition without gaps.

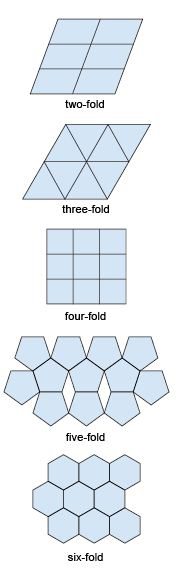
A lattice is an array of objects or points that form a periodically repeating pattern in two or three dimensions. In a crystal lattice, the repeating pattern is simply an arrangement of atoms (or ions) that is located at regular points, called lattice points.

Figure 23a shows a three-dimensional lattice, the building of which can be envisaged by simply stacking a series of identical two-dimensional lattices on top of each other. A crystal is, in effect, a structure formed by countless numbers of identical tiny building blocks, called unit cells (Figure 23b), and these make up the crystal lattice. Each mineral has a specific unit cell, which is defined according to the lengths of its sides and their angular relationships. Each unit cell contains one or more different kinds of atoms joined to each other by chemical bonds. Shapes of unit cells vary from one mineral to another; all have six sides (three sets of parallel faces, though not necessarily perpendicular to each other).

Figure 23 Anatomy of a three-dimensional lattice. (a) Stacking two-dimensional lattices results in a three-dimensional lattice made of tiny 3D building blocks. (b) The 3D unit cell is the basic building block of the crystal lattice. Its shape is defined in terms of the lengths of the sides and the angles between them. (c) Angles between the three crystallographic axes.

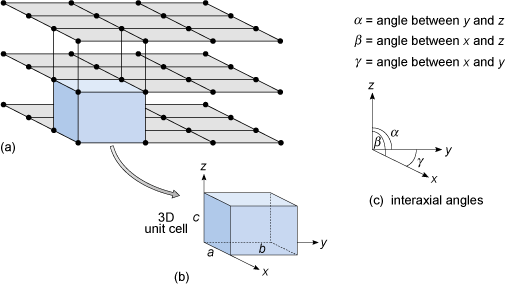
To define the resulting three-dimensional lattice, it is convenient to specify reference directions, x, y and z, which are chosen to be parallel to three edges of the unit cell (Figure 23b). These are known as crystallographic axes, and it is important to realise that they are not always at 90° to each other. The angles between the axes are denoted by the Greek letters α, β and γ (alpha, beta and gamma), as shown in Figure 23c. The size of the unit cell is given by the lengths of the three edges, a, b and c, as shown in Figure 23b. The unit cell is extremely small - typically less than 1 nm (10⁻⁹ m) in any direction. It is therefore a huge jump in scale from a single unit cell to a single crystal visible to the naked eye. With an edge length of 1 nm, a crystal only 1 mm³ requires 10¹⁸ unit cells to build it: a vast number.

A three-dimensional lattice (which may have billions of lattice points) can be represented by just six numbers: the lattice parameters a, b, c, α, β and γ. In the next section, you will see how the shape of the unit cell relates to a crystal's symmetry, and what this means for the external shapes of crystals.