5.3 Viscoelasticity and master curves

An immediate consequence of the viscoelasticity of polymers is that their deformations under stress are time dependent. If the imposed mechanical stress is held constant then the resultant strain will increase with time, i.e. the polymer creeps. If a constant deformation is imposed then the induced stress will relax with time (stress relaxation). Figure 46 shows the creep strain response to a constant stress followed by unloading. Note that in the recovery stage the strain has still not returned to zero even a considerable time after the stress has been removed.

Figure 46 The creep strain response of a viscoelastic material subjected to a constant stress of finite duration

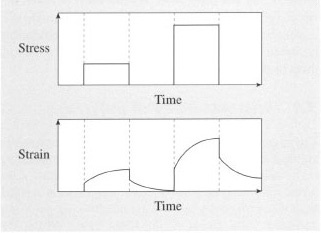
There are many examples of products which creep in service. For example, the plastic tub of an automatic washing machine will successively creep and recover as it is loaded and unloaded several times during the washing cycle. Viscoelastic stress analysis during the design of the tub ensures that the maximum strain due to this loading pattern is well within the strain limits for the material and the application.

The creep and stress relaxation properties of a polymer can be described by the time-dependent moduli E_c (t) and E_R (t). The creep modulus is the ratio of an imposed constant stress σ₀ to the time-dependent strain ε(t)), while the stress relaxation modulus is the ratio of the time-dependent stress σ(t) to an imposed constant strain σ₀, i.e.

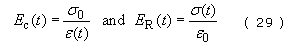
Practical examples of the need to design for stress relaxation are in seals where the sealing force must remain adequate under conditions of constant deformation, or when a metal peg needs to be held in a plastic block by push fitting into an undersized hole. The oversize peg results in a constant hoop strain in the plastic. The corresponding hoop stress will decay with time but must always be sufficient to hold the peg in place. Both creep and stress relaxation are factors that have to be considered in design, although they are not necessarily always deleterious (see Box 11).

E_R (t) is characteristic of the polymer concerned at a particular strain and temperature. It is the tensile stress relaxation modulus if the corresponding strains and stresses are tensile. Alternatively if the strains and stresses relate to shear or hydrostatic changes then the corresponding material parameters are the shear and bulk relaxation moduli respectively. As noted earlier, for polymers, the tensile modulus should not be referred to as Young's modulus. Young's modulus is the limiting case of the tensile modulus when the induced strains can be considered infinitesimal and independent of time.