5.4 Dynamic mechanical properties
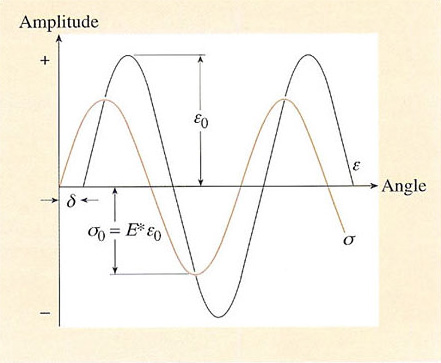
Viscoelasticity is not experienced just under quasi-static conditions, i.e. when the imposed stresses and strains are constant or change only slowly. Polymers, and particularly rubbers, are often deliberately selected for products which are to be subjected to dynamic mechanical loading. Tyres are an obvious example where the unique high strain elasticity and energy absorbing qualities of rubbers make them the natural choice of material. Stress analysis involves the use of the frequency-dependent dynamic moduli of the polymers. Assume, for example, that the polymer is subjected to a sinusoidal stress σ of amplitude σo and frequency ω, i.e. σ = σ 0 sin ωt. Stress analysis concerned with the dynamic mechanical properties normally assumes that polymers are linearly viscoelastic. Hence the strain response e to the imposed sinusoidal stress can be described as ε = ε 0 sin (wt − δ) where δ is the phase angle. This is shown diagrammatically in Figure 50.
Note that the strain response lags behind the stress by the phase angle – owing to the viscous component of the material. Some, but not all, of the energy stored during the deformation of the material is dissipated. Since the material is assumed to be linear, the stress is proportional to the strain at all times, i.e. σ = Eε, but E is a function of the frequency ω. Because the stress and strain are not in phase, E must be treated as a complex function:

where ![]() , and E″ and E″ are the in-phase and out-of-phase components of the modulus.
, and E″ and E″ are the in-phase and out-of-phase components of the modulus.
From the above definitions of the dynamic moduli and by manipulation of the linear relationship between the sinusoidal stress and the corresponding strain response, the phase angle δ can be expressed as follows:

Tan δ is commonly called the loss tangent or damping factor. E″ and tan δ are the most commonly measured dynamic properties of rubbers, representing the elastic stiffness and damping or hysteresis properties respectively. Figure 51 is a schematic representation of E′ and tan δ as a function of frequency for natural rubber, and shows the effect of crosslinking on damping and hence heat dissipation. Different rubbers will have different curves, and some care is needed in rubber product design to match the material with expected imposed frequencies. Fillers such as carbon black will also affect the shape and position of the damping maximum. Sometimes the ‘argument’ of the complex modulus |E| is used instead of E*, and is given by the equation
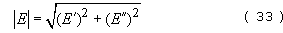
At very high frequencies (ω = 104−108 cycles s−1 or Hz) rubber is very stiff with a glass-like modulus. At these frequencies the polymer molecules do not have time to react in response to the forcing oscillations. The damping factor is then small but it increases to a maximum value in the ‘leathery’ transition region between the glassy modulus and the usual (low) modulus which is characteristic of rubbers that are deformed slowly (ω 1 cycle s−1 or Hz).
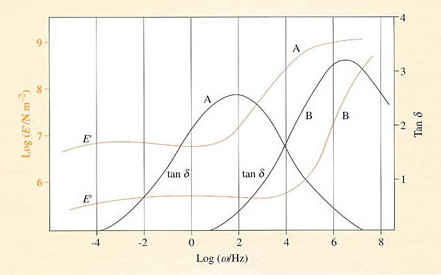
It will be noticed from Figure 51 that decreasing the frequency of oscillation imposed on the material is equivalent to increasing the temperature (glass-like behaviour is experienced at high frequencies). This is another manifestation of viscoelasticity, in which the effect of the three basic variables, time (t), temperature (T) and frequency (ω), on a polymer are all closely interrelated. Since decreasing the time scale of an experiment is equivalent to decreasing the temperature (Figure 47 and the WLF Equation (30)), so decreasing the frequency is equivalent to increasing the time scale (and hence increasing temperature).
Self assessment question 10
What is the effect of increasing the speed of a car on the rubber material of the tyre treads? Use the WLF equation and time-temperature superposition principle to justify your argument.
Assuming that a car tyre is 0.3 m in diameter, evaluate the effect of increasing car speed on the dynamic properties of the tread material (use Figure 51 as a source of information on the material of the tread). What other factors might you need to take into account to evaluate the dynamic properties?
Answer
Increasing the speed of a car means increasing the rate of rotation of the car wheels. The frequency of rotation, ω, will thus increase with speed, and this increase in ω will be imposed on the rubber of the tread in direct contact with the road. From the WLF equation and the time-temperature superposition principle, an increase in ω is equivalent to a reduction in time scale, t or a reduction in temperature; the rubber will become stiffer as the speed increases. Heat dissipation may also increase as the maximum in tan δ is approached (Figure 51).
Note that the frequency is shown in the figure as a logarithm term, so that maximum heat dissipation will occur at a frequency of 102, or 100 cycles per second for the well-crosslinked NR compound. For a car tyre about 0.3 m in diameter, then since the circumference is
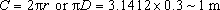
Thus 1 Hz or 1 cycle per second, is equivalent to a car speed of about 1 m s−1, or about 3.6 kph. A frequency of 100 Hz is thus equivalent to 360 kph, a speed normally well above the capabilities of normal saloons! However, the diagram shows that heat dissipation will increase rapidly with increasing speed, and in adverse conditions (dry road, rough surface) could lead to tyre burn and tread loss. Wet conditions will help to absorb any heat in the tyre, and a rough road will increase the effective frequency of deformation of the tread by imposing extra vibrations on the structure.
The rubber used in the tread will be important in evaluating heat loss, as will the presence of any fillers, especially carbon black. Crosslink density will also be important in controlling the response of the tyre (Figure 48).
