3.3 Sampling a continuous-time signal

To convert a continuous-time signal into its discrete-time signal equivalent, you need to sample the waveform. To ensure the discrete-time signal contains the full range of frequencies in the continuous-time signal, the continuous-time signal normally needs to be sampled at a rate that is greater than twice the highest frequency component contained in the signal. The lowest sampling frequency that can fully reconstruct the continuous-time signal is called the Nyquist frequency after Harry Nyquist (1889–1976), a Swedish-born American engineer who made important contributions to communications theory.

What happens if the sample rate is equal to or less than twice the highest frequency in the signal – or, to express this another way, if the continuous-time signal is sampled twice or less than twice within each cycle of the highest frequency component contained in the signal? Figure 16(a) shows a sine wave (solid line) that is being sampled less than twice each cycle. The samples are represented by blobs. However, another sine wave with a lower frequency can be drawn through these samples. It is shown as a dashed sine wave. This lower-frequency wave is called an alias of the original sine wave. The way to avoid aliases is to sample more frequently, as in Figure 16(b). Here there are twice as many samples as in Figure 16(a). Now the alias from (a), also shown dashed in (b), misses some of the samples in (b). There is no waveform of a lower frequency than the sampled waveform that can be fitted to all the samples.

Figure 16 (a) More than one sine wave can be drawn through these samples, so there is a low-frequency alias of the original wave; (b) with more samples, there is no alias that can be fitted to all the samples

Show description|Hide description

This figure consists of two graphs. Each one shows a sine wave being sampled. The sine wave is drawn above a horizontal axis. A series of evenly spaced vertical lines, representing the samples, extend from this axis to the sine wave. Each line has a small filled circle at the point where the line meets the wave.

In graph (a), seven samples are taken for five cycles of the sine wave. A single cycle of a lower-frequency sine wave is drawn through all seven filled circles, showing that there is an alias.

In graph (b), thirteen samples are taken for five cycles of the sine wave. The lower-frequency sine wave from graph (a) is shown again, but it does not pass through all the filled circles.

Figure 16 (a) More than one sine wave can be drawn through these samples, so there is a low-frequency alias of the original wave; (b) ...

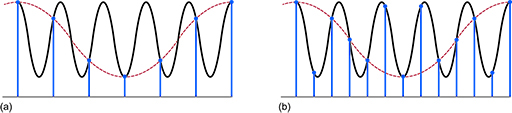
The way to eliminate the possibility of an alias is either to have greater than two samples per cycle or, conversely, to ‘band-limit’ the signal to make sure that there are no frequencies equal to or higher than one half of the sampling frequency. This is done by including an analogue filter before the sampler in the analogue-to-digital converter that removes all frequencies higher than a certain frequency. As such, a filter is designed to stop any chance of aliasing occurring, it is sometimes called an anti-aliasing filter.

After sampling the signal, the samples need to be converted to a digital signal. The next section describes how this is done.