Example 3 Reading a logarithmic scale
One representation that often arouses public interest is the probability of dying from different causes in a year for an ‘average person’. Figure 13 compares the risks associated with a number of differing possibilities.
Reading these probabilities is a little challenging because of the logarithmic scale. The trick is to remember that this scale behaves normally if you calibrate it with respect to the exponent. So the first step is to read the value off the scale as if it were just calibrated in terms of the power of ten. This is demonstrated in Example 3.
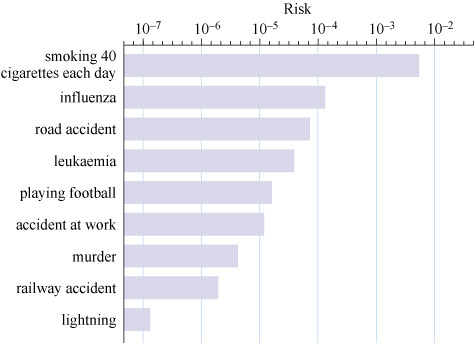
Use Figure 13 to estimate the probability of dying from influenza.
Solution
The bar representing death from influenza lies between 1 × 10-4 and 1 × 10−3, with an exponent of about −3.9. So you need to find the value of 10−3.9.
Using a calculator to convert this to a number (in many calculators this is done by typing 3.9, changing the sign, and then pressing the button marked ‘10x’, but other calculators may use a different sequence) gives 1.258… × 10-4.
It’s difficult to estimate the uncertainty in this figure (you could enter estimates of the upper and lower limits and calculate the values), but it’s unlikely to be much better than 3 significant figures.
So the risk of dying from influenza is approximately 1.26 × 10−4.
Activity 4 Estimating probability
Use Figure 13 to estimate the probability of dying from
- a.smoking 40 cigarettes each day
- b.playing football.
Roughly how much more likely is it that a heavy smoker will die in a given year than a non-smoking football player?
Answer
From Figure 13:
- a.The risk of death from smoking 40 cigarettes each day is approximately
1 × 10−2.3 = 5.01 × 10−3 (to 3 significant figures – s.f.).
- b.The risk of death from playing football is approximately
1 × 10−4.8 = 1.58 × 10−5 (to 3 s.f.).
The ratio of the two risks is given by
So smoking is approximately 316 times more dangerous than playing football. This ignores the health and social benefits of playing football (due to the exercise and interactions with other people), which will also offset the risk. Note that the result is extremely sensitive to small changes in the values you selected for the exponents so your answers may well be different from these.
Notice that two potential causes that often excite media interest and public comment – murder and railway accidents – are both relatively unlikely. By comparison, smoking and influenza are relatively common causes of death. It is such perceptions that make the identification of acceptable risk so difficult.
An estimate of the probability of a catastrophic accident in a nuclear power station has been put at once every 10 000 years – catastrophic being something like the incident at the Chernobyl nuclear reactor in 1986, when there was a large release of radioactive material. (Note, though, that the safety of nuclear reactors has improved considerably since the Chernobyl reactor was designed. All current indications are that the Fukushima nuclear incident following the tsunami off the coast of Japan in 2011 was far less severe than Chernobyl.) This probability figure of 1 in 10 000 years (or 0.0001 per year) sounds reassuring, but remember that it is for a single reactor. In mid-2016, there were about 450 civil nuclear reactors operating across the world.
Regulators apply what is known as the de minimis concept, which assumes that there is a level of risk that is so low it can be reasonably ignored. Its name is derived from the common law maxim de minimis non curat lex: ‘the law does not concern itself with trifles’. A one-in-a-million level of increased risk over a lifetime is often used as a reasonable criterion for separating high-risk problems (which warrant attention) from negligible-risk problems (which do not). Of course, you can try to quantify such risks, but still your perception of whether that is acceptable might differ from someone else’s.
