3.2 Room to rattle: modelling thermal expansion
In general, as the temperature of a piece of solid is raised the volume it occupies increases. I say 'in general' because as we shall see it is not always the case, and we ought to investigate whether we can exert any control over the phenomenon – which could be useful. Evidently, if a solid expands, the average spacing between its constituent parts must have increased. Since matter is made up of atoms, the issue is really about the volume occupied by the arrangements of atoms that make up any particular solid.
First, it's a good idea to remember that in a solid, atoms are held together by a network of bonds. The nature of these bonds can be classified into three distinct, strong types (ionic, covalent and metallic), though often in practice the bonding within a material may contain characteristics of more than one type. In addition, there are often weaker, secondary bonds between atoms. For the present it is enough to say that atoms are bonded together in a way that holds any pair of atoms at a particular separation, measured from the centre of one atom to the centre of another. Figure 4 illustrates this for a simple plane of identical atoms – fully three-dimensional networks are more realistic but less easy to draw.
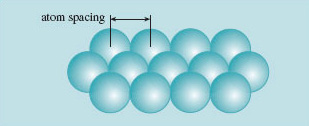
What happens if we try to force the atoms closer together, say by compressing the solid, squeezing it uniformly from all sides? Well, apparently there are strong forces that oppose this, almost as if the atoms were hard spheres; most solids are pretty incompressible. What happens if we try to pull the atoms apart then? Once again, the bonds resist, attempting to maintain the spacing as if the atoms were 'glued' one to another.
So where does temperature come into the story? The equilibrium spacing, that is the distance between atom centres, is in fact determined by the way electrons around each atom interact with those of neighbouring atoms. The model of solids I am describing is not quite one with hard spheres glued together – it's a bit more subtle. For a start, the atoms are not stationary but vibrating around their mean position. The vibration is a consequence of their thermal energy. So the thermal energy of the atoms interacts with the binding energy of the electrons that hold the atoms with a particular spacing. A more sophisticated picture is therefore one of an assembly of atoms that rattle around mean positions in the network.
The model needs to link 'more atomic kinetic energy (temperature)' with 'bigger spacing'. The way we can do this is to associate the amplitude of vibration with thermal energy and thence to temperature. In effect, as thermal energy is added to a solid, the atoms tend to occupy a bigger volume. It turns out that it's much harder to squeeze the atoms closer together than it is to pull them slightly further apart, so larger-amplitude vibrations will tend to push atoms further apart to create the space in which to rattle about.
Thermal expansion is a property that is reasonably well described by this model. The length of a line of atoms in a plane of atoms at any instant of time is now the sum of many different atom spacings, owing to those vibrations. The average spacing will be greater if the amplitude of vibration increases. Thus thermal expansion fits into the model.
That's the model. How does it work in practice? It works best for denser materials like metals with their close-packed atom structures. In the relatively open crystals and glasses formed from inorganic compounds, distortions of the crystal structure can accommodate some of the increase in average spacing. Consequently these materials show rather lower expansion coefficients α – compare soda glass, porcelain and silica with the metals in Table 4. And there are ways of otherwise coping with thermal expansion. See Box 3 Invariant metals.
Example 2
Using data from Table 4 below, calculate the following changes in dimension that result from uniform temperature changes:
(a) the changes in length, width and thickness of an alumina tile that measures 30 mm × 10 mm × 0.5 mm after it has been heated uniformly by 200 °C;
(b) the change in volume and density of the same alumina tile.
Answer
(a) The linear model of thermal expansion suggests that the change in dimension is:
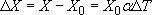
and we need to apply this separately to the three dimensions, L, H, W, noting that a change of 1 °C is the same as a change of 1 K:
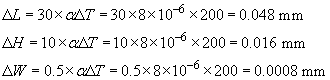
Each dimension is 0.16% larger (αΔT = 1.6 × 10−3).
(b) The original volume was 30 × 10 × 0.5 = 150 mm3
The new volume is 30.048 × 10.016 × 0.5008 = 150.721 mm3. The volume of the hot tile is thus 0.721 mm3 larger, which is an increase of (0.721/150) × 100 = 0.48%. Notice that each dimension contributes 0.16% to the net volume change, which is effectively 3 × 0.16%. The mass is unchanged, so the density must have decreased by 0.48%.
SAQ 2
Using data from Table 4, determine the following:
(a) the change in circumference of a thin hoop of steel having a diameter of 1.200 m after it has been uniformly heated by 300 K;
(b) an estimate of the change in length of a rod of soda glass that is originally 10 mm long after one end has been heated by 400 K (assume that the temperature of the rod varies linearly from the cool end to the hot end, and work with the average temperature change of the rod).
| Material | α/10−6 K−1* | Material | α/10−6K−1* |
|---|---|---|---|
| Invar | 0.1 | nickel | 14 |
| fused silica | 0.5 | stainless steel | 16 |
| porcelain | 2 | copper | 17 |
| brick | 7 | tin | 18 |
| alumina | 8 | brass | 21 |
| soda glass | 9 | aluminium | 24 |
| steel | 11 | lead | 30 |
| concrete | 12 | nylon | 100 |
*The heading 'α /10−6 K−1' can be read as 'alpha, in units of 10 to the minus 6 per kelvin'. The numbers in this column must be multiplied by the unit in the heading to get the full numerical value. Thus the expansion coefficient for porcelain is 2× 10−6 K−1.
Answer
(a) The length of the circumference of the cool hoop is πd, whereas the hot hoop circumference will be (1 + αΔT) times longer, making it πd(1+ αΔT) – that is, an increase of (dαΔT. It is as if the diameter had linearly expanded on heating; take care though, as we have been able to neglect the change in thickness of the thin strip from which the hoop is made. Thus, the circumference expands by an amount
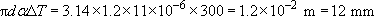
(b) Since only linear changes are involved we can determine an average expansion of the whole rod, as if it were all at the temperature at the midpoint, i.e. 200 K hotter than the initial condition. So, using α=9 × 10−6 and ΔT = 200 K, the rod will be longer by αΔT × 10 mm = 1.8 × 10−2mm.
Box 3 Invariant metals
Invar®, an alloy containing 64% iron and 36% nickel, has a minute coefficient of expansion at room temperature of 0.1 × 100−6 K−1, which is less than 8% of the coefficient of either of its constituents. It is described as being (almost) invariant. What could be compensating for the thermal effect? The answer is in the temperature dependence of a magnetic interaction of the atoms; iron and nickel are both magnetic materials. For this particular alloy the rate at which the magnetic coupling slackens with temperature and allows the chemical bonding to pull the atoms closer just balances the normal thermal expansion effect. The alloy was discovered by Charles-Edouard Guillaume in 1899 and immediately replaced an awkward bimetal method of expansion compensation in clock pendulums (Figure 5).

Guillaume went on to discover Elinvar in 1912. This alloy, 35% Ni, 10% Cr, 55% Fe, has zero temperature coefficient of Young's modulus. Elinvar – elastic invariant – solved the worst problem of inconstancy of spring-driven balance wheels in watches, which was that the elasticity of the spring decreased with rising temperature and slowed the watch. A combination of a berylliumbronze wheel and an Elinvar spring allows a simple structure whose oscillation is temperature independent, with expansion and elastic effects compensating one another. If the new alloys had been more expensive they might not have been favoured. It would be nice to think that the principle described led to the discovery, but the explanation came after the discovery.
Guillaume's alloys found application in clocks, watches and other precision instruments, and led to the award of the Nobel Prize for Physics in 1920.
