4.2.3 The significance of the distribution of energies
Near room temperature (300 K), the average bundle of thermal energy associated with a particle is 0.026 eV (look back at Box 2 Temperature and energy). This is not going to do much damage to something stuck together with bonds that have an energy of a few eV – just as the average wage earner can't participate in an auction of fine art. Look back at Figure 13(b), however, and notice that the distribution of energies extends further up the energy axis. Particles with much higher energy than the average may well be able to break free of their bonds and to initiate major changes in the bulk properties of the material of which they are a part. Though relatively few in number, in a population of millions you will always come across some particles with many times the average energy. It is important to know more about particles in the high-energy tail of the distribution of energies I sketched in Figure 13(b). In particular, how does their number change when the average energy increases?
Figure 14 shows two schematic thermal distributions with different average values. I have put a real energy scale on the horizontal axis; the vertical axis shows the number of particles, N(E), with energies in a narrow band close to E. The total number of particles is represented by the area under the curve, and both curves represent the same number of particles.
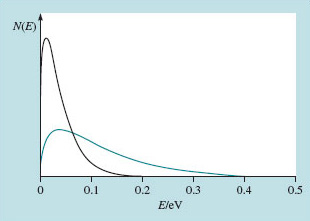
The taller, narrower of the distributions in Figure 14 represents an energy distribution at a temperature of 300 K. The shorter, broader one represents a distribution at a temperature of 900 K. You can see that whereas at 300 K you cannot detect any particles having an energy above 0.2 eV, at 900 K –you might say three times hotter – several per cent of the particles have energies that exceed 0.2 eV. Extending this argument, it can be shown that at 2000 K, around one per cent of particles in such a distribution would exceed 1 eV. Although the full story of melting is more complicated, it is not too surprising that 2000 K is enough to shake many solids to bits.
