4.3.1 Arrhenius's law
In 1889 Arrhenius, a Swedish chemist, put forward a model to describe the way in which the rates of many chemical reactions could be accelerated by increasing temperature. His model is based on the idea that the rate at which such chemical reactions happen is proportional to the number of particles with enough thermal energy to overcome some sort of energy barrier. In other words, it relates the rate at which things happen to the fraction of particles having energies beyond some threshold energy. This threshold is characteristic of the process and is called an activation energy, E a, for whatever process is involved. The rate, r, is therefore:
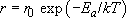
In Arrhenius's model, the pre-exponential scaling factor, r 0, is a constant. Arrhenius's law has subsequently been found to apply in general to thermally activated processes such as diffusion (see Box 9 Carburizing steel) and the conductivity of ceramics (see Box 10 Thermistors).
SAQ 5
Calculate how much faster a particular chemical reaction will proceed at 500 K compared with the rate at 300 K, if the activation energy of the reaction is 0.4 eV.
Answer
The rate at which the chemical reaction will proceed at 500 K is
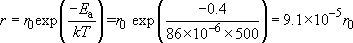
The rate at which the chemical reaction will proceed at 300 K is

We don't need to know r0 to get the ratio of the rates, which is

