4.3 Possible solutions
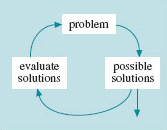
According to Figure 7, our map of the problem-solving process, once we've defined the problem according to the need the next step is the creative bit – to look for 'possible solutions', Figure 10.
Depending on the need, this may require innovation by context, innovation by development or a routine solution. Contrary to what you might expect, innovation is not the only interesting or challenging option – there may be any number of potential solutions using standard parts, but only one really elegant combination. As good engineers, in an ideal context (remember this point), we are not just looking for a solution; we are looking for the best solution. However, although practising engineers will be looking for the best solution, they do not always have the time or resources actually to reach it. Even if they did have as many resources as they wished, it might still not be possible to know what the best solution is, or whether it has been reached. So if the engineer cannot know when 'best' has been reached, we see that compromise is an abiding characteristic of solving engineering problems.
Creative thought has to come without inhibition, influence or bias, and if you consider how difficult that is in the light of the problem in SAQ 3, then it makes sense that we shouldn't just expect it to happen. We can exercise our brain in much the same way as we exercise our bodies, and we can sharpen particular abilities by repeated action of the same or similar process. There are whole courses available in finding creative solutions, working up from simple questions to complex theoretical posers. The more you practise 'thinking outside the box', the better you will become. Foster, in a book called How to Get Ideas, has a good summary:
Think laterally. Think visually. Play “What if?” Look for analogues. Look for things to combine. Ask yourself what assumptions you're making, what rules you're following. Screw up your courage and attack.
Foster (1996) p. 159
This is fine for working alone and stimulating your own creativity with no one around to question your ideas. In most commercial or industrial situations, however, you are more likely to be working as part of a group or team. Here, the so-called brainstorming approach is popular. There need not be a hierarchy within a brainstorming group – you mix contemporaries from different disciplines or representatives of other departments, with the assurance that each member is accorded respect and allowed to express suggestions 'without prejudice'. In a group situation everyone should feel totally at ease, free to put forward any idea that occurs, however lateral, apparently silly or unlikely. Next, the group is at liberty to ask questions and put the idea up for enquiry, but reasons to discard any idea must be rational and valid. Thus the atmosphere, relaxed and receptive, is open to completely new and innovative solutions.
Not all engineering is about innovation. Techniques such as brainstorming, used as above, and creating Spider diagrams of ideas, are a way of bringing ideas together, but not all the ideas will be original.
Box 6 Spider diagrams
A technique widely used for stimulating free thought is the spider diagram (sometimes known as a spray diagram). It works on the principle of removing the hierarchy of importance, implied when items are written in list form. Instead, the title of the problem or need is put at the centre, and as items are thought of, they are placed in more or less random positions on the paper. The connections between related items are then represented by lines, to produce a multi-limbed structure that gives the diagram its name. Usually, the process of drawing the relationships between items stimulates the addition of further items. Once the relationships have been made, it is possible to group several items together in themes, and a tree-like structure emerges. The diagram is now useful as a map of the whole topic, its critical issues, and the relationships between them. Figure 11 is an example.
In all but the most 'blue sky' organisations, constraints are present in terms of cost, time, capacity, environment, manufacturing capability – you think of it, it's a constraint. Add to this the limits imposed by our knowledge of the physical world – things like data storage capacities, material, fluid or gas properties, Anthropometrics and ergonomics and so on – and the problem up for attention has either shrunk significantly or has become more complex.
Box 7 Anthropometrics and ergonomics
An engineer uses anthropometric data when designing something that will be operated or used by a person, or rather more specifically, by any unknown person. It represents the weight and measurements of the average man, woman and child, usually presented in centiles (the 50th centile being the median average), and covers everything from basic height to the length of a little finger.
What the average person can do, on the other hand, is presented as ergonomic data. This is about how hard we can push, what pressure we can exert on a foot pedal, the most comfortable reach, etc. In the same way that we use tables of data for solid, gas or fluid properties in the specification of materials, we use anthropometrics and ergonomics to design for people.
Tables 2 and Tables 3 show the kind of information that is typically gathered and used.
| Male | Female | |||
|---|---|---|---|---|
| Body dimension | Mean/mm | SD*/mm | Mean/mm | SD*/mm |
| Stature | 1740 | 70 | 1610 | 62 |
| Eye height | 1630 | 69 | 1505 | 61 |
| Shoulder height | 1425 | 66 | 1310 | 58 |
| Elbow height | 1090 | 52 | 1005 | 46 |
| Sitting height | 910 | 36 | 850 | 35 |
| Sitting eye height | 790 | 35 | 740 | 33 |
| Sitting shoulder height | 595 | 32 | 555 | 31 |
| Sitting elbow height | 245 | 31 | 235 | 29 |
| Thigh thickness | 160 | 15 | 155 | 17 |
| Buttock-to-knee length | 595 | 31 | 570 | 30 |
| Buttock-to-popliteal length | 495 | 32 | 480 | 30 |
| Knee height | 545 | 32 | 500 | 27 |
| Popliteal height | 440 | 29 | 400 | 27 |
| Shoulder breadth (bi-deltoid) | 465 | 28 | 395 | 24 |
| Hip breadth | 360 | 29 | 370 | 38 |
| Chest (bust) depth | 250 | 22 | 250 | 27 |
| Shoulder-to-elbow length | 365 | 20 | 330 | 70 |
| Elbow-to-fingertip length | 475 | 21 | 430 | 19 |
| Forward grip reach (from the back of the shoulder blade) | 780 | 34 | 705 | 31 |
| Upper limb length | 780 | 36 | 705 | 32 |
*SD=standard deviation, representinga statistical departure from themean value.
| Thumb | Index finger | Middle finger | Ring finger | Little finger | |
|---|---|---|---|---|---|
| Mean force/N | 17 | 11 | 10 | 8 | 5 |
| Range/N | 14–20 | 8–14 | 8–12 | 5–10 | 3–9 |
SAQ 4
The back of a particular airline seat is 100 mm thick. Explain why it would be unreasonable to install 12 rows of seats in a cabin with a floor length of 7 m. Suggest, with a brief justification, a more reasonable number of rows.
Answer
The space available per seat with 12 rows in 7 m would be
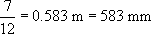
Of this, 100 mm must be allowed for the seat back, leaving just 483 mm for passengers' legs. According to Table 2, the mean buttock-to-knee length of an adult male is 595 mm and that of women is 570 mm. Thus, there is insufficient space for an average man or an average woman.
A more reasonable capacity might be based on the mean, male, buttock-to-knee length (595 mm) plus one standard deviation (31 mm), plus the depth of the seat back (100 mm) for each seat. That amounts to 726 mm per seat. The number of rows would then be 7000/726 = 9.6; in practice this would need to be rounded down to 9 rows with 777 mm per seat.
For comparison, typical economy-class seat spacings are 710 to 860 mm, and the UK Civil Aviation Authority's current minimum (under review) is 660 mm.
The search for solutions must involve a thorough appreciation of the problem. It may involve detailed analysis and calculations based on scientific and engineering principles and using technical data. This is mathematical modelling, and it is useful at many stages in the process of identifying solutions; it is specifically addressed later in Section 4.5.
In practice then, finding a solution is usually a delicate balance between finding 'the best design' and getting something into the market-place 'by yesterday'. Earlier on I asked you to remember a point:
As good engineers, in an ideal context, we are not just looking for a solution; we are looking for the best solution.
Now you see why I added the condition about context. I think that any course that hopes to contribute to the formation of professional engineers has a responsibility to make this clear. Over the duration of an engineering qualification, you will learn a little about many of the tools you need to solve problems. You are likely to specialise, and learn more about, say, mechanical, civil or electrical engineering, building services, software, chemical processes, nuclear power and so on. It would be impractical to expect you to study every problem-solving technique tailored to every conceivable context. However, a good course of study will make sure that you are aware of the constraints that we have discussed above, and that you have some practice in bringing together maths, science or technology in ways that create practical, physical solutions. That way, when you call on your skills 'for real', you won't be surprised when your 'best' solution is ditched in favour of the one that has a quarter of the durability but costs half the money and can be made within the organisation. Instead of being depressed about this, understand and use those constraints to shape your next design; if you know that such limits will be imposed, make them your goals and work to achieve them.
Getting back to our problem-solving diagram, you may have noticed that Figure 10 shows another circuit – a loop from possible solutions, to evaluating solutions, and back to the problem. You may also remember that the problem is linked back to a need (Figure 8), and so at this stage any suggestion may take you right back to the start, asking new questions about the need and refining or redefining the problem, quite possibly by going back to the customer. The trick here is not to redefine the problem in order to suit your solution, but to be sure that your solution is meeting the need.
