10.3 The decibel as a measure of sound amplitude
As I mentioned earlier, because a decibel is a way of expressing a ratio, it cannot by itself express the absolute size of anything. To express absolute values it must be referred to a fixed reference quantity, against which whatever is being measured can be compared. In the context of acoustics the reference used is the lower limit of audibility – the threshold of audibility. This varies from person to person, but has a nominal value that can be expressed as a pressure wave with an amplitude of about 0.000 000 01 per cent of atmospheric pressure. This is taken to be 0 dB. If a sound level is described as being ‘40 dB’, it means that its amplitude is 40 dB relative to the agreed threshold of audibility. This means that its amplitude is 100 times greater than that of the audibility threshold. Sound amplitudes expressed in decibels in this way are said to have a sound pressure level (SPL) of so many decibels (see Box 5).
Box 5: Sound pressure level
The sound pressure level (SPL) in decibels of a sound with a given pressure amplitude is:
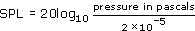
The figure of 2 × 10 −5 in the denominator is the amplitude in pascals of a pressure wave at the lower limit of audibility at a frequency of 1 kHz.
Activity 33 (Self-Assessment)
The amplitude of a sound is 1000 times greater than the reference value. What is its sound pressure level in decibels? Use either the graph in Figure 27 or Table 1.
Answer
From Table 1 or from the graph, an amplitude ratio of 1000:1 is equivalent to 60 dB. This is the sound pressure level of this sound.
The following activity is designed to give you a flavour of what a change in sound pressure level of a few decibels corresponds to.
Activity 34 (Listening)
Listen to the audio track below, where you will hear a sine wave in which the sound pressure level changes in 3 dB steps. You might like to compare it with the first part of the audio track of Activity 30 where the sound pressure level changed in 6 dB steps.
Click 'Play' to listen to Audio Clip
Activity 35 (Self-Assessment)
I mentioned earlier that a sound level that was a million times greater than the threshold of audibility would be distressingly loud for most people. Given that 0 dB is the level assigned to the threshold of audibility, use Table 1 and the additive property of decibels to find the sound pressure level of such a loud sound.
Answer
Table 1 does not give us a decibel equivalent directly for an amplitude ratio of a million to one. However, Table 1 shows that a ratio of 1000:1 has a decibel equivalent of 60 dB. Hence 1000 000, which is 1000 × 1000, has a decibel equivalent of 60 dB + 60 dB, which is 120 dB. This sound pressure corresponds to a jet taking off when heard from a distance of 100 m.
Table 3 gives some approximate sound pressure levels. You might be surprised at how loud some instruments are. We do not normally think of the violin and flute as loud instruments. However, because of the close proximity of the player's ear to the sound source, sound pressure levels for the performer are not far from levels that can damage the player's hearing. Frequent, extended playing of these instruments at high volume, as may happen in orchestras, can result in hearing loss for the player. Players of other instruments, particularly brass instruments, are similarly at risk, as are users of personal stereo systems with headphones if they are regularly used at high volume.
| Sound | Sound pressure level |
|---|---|
| Threshold of hearing | 0 dB |
| Breeze through leaves | 10 dB |
| Empty concert hall | 20 dB |
| Bedroom | 30 dB |
| Domestic living room | 40 dB |
| Office noise | 50 dB |
| Conversation at 1 m | 60 dB |
| Piano practice | 60–70 dB |
| Car interior/Singer fortissimo at 1 m | 70 dB |
| Chamber music in small auditorium | 75+ dB |
| Heavy car traffic at about 10 m | 80 dB |
| Violin, flute at player's ear | 85+ dB |
| Orchestral music during loud passages, experienced by | 90+ dB |
| performers (permanent hearing damage on prolonged exposure) | |
| Rock performance at close range | 100+ dB |
| Timpani and bass drum rolls | 106 dB |
| Peak levels in dance club | 110+ dB |
| Jet taking off at 100 m | 120 dB |
| Threshold of pain | 130 dB |