3 Frequency
3.1 Frequency and period
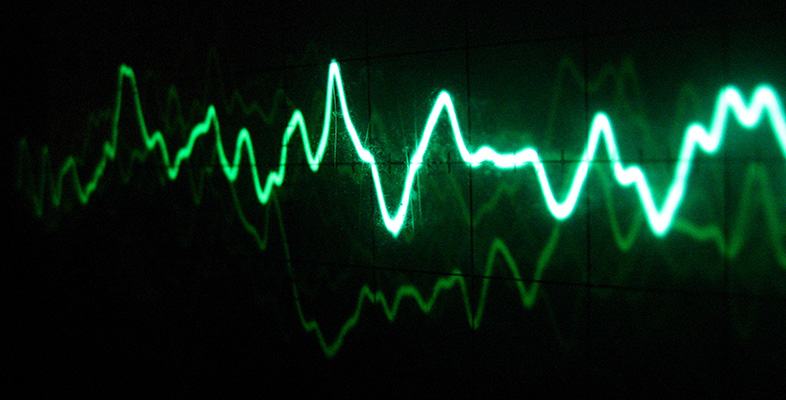
In Figure 11 you saw that waveform (b) had a much shorter period than waveform (a). Hence waveform (b) completes more cycles of oscillation in a second than does waveform (a). Waveform (b) is said to have a higher frequency than waveform (a). The frequency of an oscillation (usually represented by the symbol f) is the number of cycles there are in a second. This may or may not be a whole number. For instance, a certain wave might have 25.5 cycles in a second; another might have exactly 100. In either case, though, the number quoted is acceptable as a frequency.
The unit of frequency used to be ‘cycles per second’, which had the merit of being self-explanatory. Nowadays it is given the internationally agreed unit hertz (symbol Hz), named after the German physicist Heinrich Hertz (1857–1894). A typical tuning fork might have a frequency of oscillation of 440 Hz (or 440 hertz), meaning that the prongs perform 440 oscillations every second. For high frequencies the kilohertz is often used as a unit of frequency. One kilohertz (1 kHz) is a thousand hertz. (Larger units than the kilohertz are not required for sound, although they may be used in connection with equipment used in sound technology.)
The frequency of an oscillation is directly related to the period of the oscillation. Suppose a source of pressure waves vibrates at the rate of 100 Hz, that is, 100 cycles per second. It is fairly clear that each cycle must last for one hundredth of a second. Mathematically we express this relationship as:
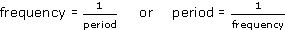
In symbols
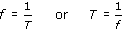
Activity 12 (Self-Assessment)
Figure 11 showed sine waves with periods of 1 second and 0.02 second. What are the frequencies of these waves?
Answer
The sine wave with a period of 1 second has a frequency of 1 Hz. The sine wave with a period of 0.02 second has a frequency of (1 / 0.02) Hz, or 50 Hz.