4.2 Frequency, wavelength and the speed of sound
The speed of sound has a joint relationship with both the wavelength and the frequency of the sound. To see why, recall that at the end of Section 2.5, in connection with the wave produced by a tuning fork, I said ‘in the time it has taken for the source to go through one cycle of oscillation, the wave has travelled a distance equal to one wavelength …’.
The time taken for the source to perform one cycle of oscillation is its period T. So, in one period of oscillation, the wave travels a distance λ. To determine the speed of the wave, we need to know how far it travels in a second, rather than in one period. In a second there are f cycles of oscillation, where f is the frequency, so in one second the wave travels f times as far as it travels during just a single cycle of oscillation. Thus:
speed = frequency × wavelength
Or, if we let the speed be represented by v:
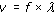
This can be restated in two other ways:
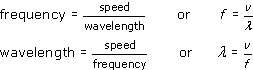
Note that when using these equations in calculations, it is necessary to specify wavelengths in metres and frequencies in hertz (rather than kilohertz or megahertz) in order to be consistent with a speed expressed in metres per second.
Activity 16 (Self-Assessment)
A tuning fork has a frequency of 384 Hz. Is the wavelength of the sound it produces greater than 1 metre or less than 1 metre? Take the speed of sound to be 340 metres per second. No calculator is needed.
Answer
The wavelength is less than 1 metre. Using λ = v/f, we can see that the wavelength in metres is 340 ÷ 384. Without using a calculator this can be seen to be less than one. In fact its value is about 0.89 metre.
The relationship v = f × λ might seem to suggest that the speed of a sound is dependent in some way on its frequency or its wavelength. But experiments show the speed to be constant (more or less). The correct interpretation of this relationship is that frequency and wavelength are inversely proportional to each other. This is what we would expect, because a tuning fork that vibrates more quickly creates high-pressure regions (and low-pressure regions) at a greater rate. The speed at which the pressure wave travels is fixed, so the regions of high (or low) pressure must pack more closely together. The equation v = f × λ shows that if one of for λ is doubled, the other must halve so that the product f × λ remains unchanged; if one is tripled, the other must reduce to a third of its former value; and so on.