2.4 How thick is Europa's ice?
You learned in Section 1.4 that geophysical data show the 'icy' outer part of Europa to be about 100 km thick, but that the information is inadequate to distinguish between the extreme possibilities of solid ice all the way down to the bedrock and a floating sheet of ice supported above a liquid ocean (Figure 13). The subdued topography of craters such as Pwyll and our interpretation of chaos regions both strongly suggest that the latter is more likely. We can determine how thick the ice was at the time of chaos formation, provided we are willing to take the present surface of the matrix to be at roughly the same height (relative to raft surfaces) as the surface of the ocean when it was exposed. The lack of any obvious disturbance of the matrix adjacent to the blocks even in the very high-resolution image in Figure 26 (see Section 2.3.4) indicates that this is a reasonable assumption. If this is correct, then the height of a raft surface above the matrix carries important information.
Question 15
Look at the rafts in Figure 24 (see Section 2.3.4). Do you get the impression that each raft has its surface at a different height above the matrix?
Answer
With the exception of the tilted rafts, they all appear to be at about the same height.
This is just a crude visual impression. However, there are various ways to determine relative heights on spacecraft images. The best way is to use the stereoscopic information contained in two images of the same area taken from different perspectives. Unfortunately, Galileo did not obtain high-resolution stereoscopic images of Europa. Instead, we can measure the widths of the shadows cast by the rafts onto the matrix, and combine this information with knowledge of the angle of the Sun above the local horizon to estimate the height of the cliff. This shows that most of the cliffs at the edges of rafts in Figure 24 are about 100 m high.
Question 16
Why would the surface of a raft (or the top of any object floating in a fluid) be higher than the surface of the matrix (or the fluid in which the object is floating)?
Answer
The only simple explanation is that the rafts are less dense than the fluid in which they were floating.
This is certainly true of ice floating in the Earth's oceans, and gave rise to the metaphor 'only the tip of the iceberg', which refers to the small fraction of something that is apparent when most of it is hidden. On Europa, the height difference can tell us the total thickness of the rafts, if we know the densities of the raft and the ocean. The principle behind this is known to geologists and geophysicists as 'isostasy' (see Box 7). (Isostasy is really just another name for buoyancy.)
Box 7: The thickness of a floating raft
Figure 27 shows a tabular raft floating at equilibrium (i.e. at its position of neutral buoyancy) in a liquid. In this situation, the pressure at the base of the raft must be the same as the pressure in the liquid immediately adjacent to the base of the raft. The formula for pressure, P, at depth d beneath a substance of density ρ is given by:

where g is the acceleration due to gravity. In the situation illustrated in Figure 27, identical pressures occur at the base of the raft, which occurs below a total raft thickness of (h + w) and at a depth w in the liquid. The difference in any atmospheric pressure between the raft surface and the liquid surface is negligible, so we can ignore this and write:
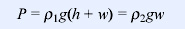
As we are interested in determining the raft thickness, (h + w), we can divide by g, to get:


We do not actually know the density of the raft (impure ice) or of the liquid (likely to be a salt solution, rather than pure water). However, we can assume a reasonable range of values, given that we can be fairly sure that the raft is mostly H2O ice and that the liquid is some kind of salty water. The density of water rich in dissolved sulfates of magnesium and sodium (for example of a composition close to that in Figure 15 in Section 2.2) would be about 1180 kg m−3. Ice freezing from such a solution could have a density as high as 1126 kg m−3 if rich in these salts or as low as 927 kg m−3 if salt-free.
Question 17
(a) Rearrange Equation 3 to find an expression for w.
(b) Use this rearranged equation to determine the maximum and minimum depths to the base of the rafts, and hence the raft thicknesses in Conamara Chaos, given that h is 100 m, ρ1 is not less than 927 kg m−3 and not more than 1126 kg m−3, and ρ2 is 1180 kg m−3.
Answer
(a) Because it is w that we are trying to find, we need to get all the terms involving w into the same side of the equation.
Equation 3 can be expanded as:
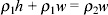
Subtracting ρ1w from both sides of this equation, we get:
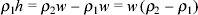
And to find w we need to divide both sides by (ρ2 - ρ1):
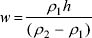
(b) It might not be immediately obvious whether the maximum raft density will give the maximum or the minimum raft thickness, but it has to be one or the other. Inserting the value of 1126 kg m−3 as ρ1 in this equation and using 100 m as h and ρ2 as 1180kg m−3, we get:
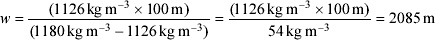
The raft thickness is (h+w), and so we need to add 100 m to this value, giving a raft thickness of 2185 m.
Inserting 927 kg m−3 as ρ1 in the same expression we get:
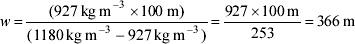
and hence a raft thickness of 466 m.
The cliff height is certainly not known to three significant figures, so we should not quote these results to more than two significant figures. Thus, according to this method, the raft thickness is not less than about 470 m and not more than about 2200 m.
In fact, the less the density contrast between raft and fluid, the lower the height of the cliffs. If a raft has the same density as the fluid it barely floats at all. If a raft is very much less dense than the fluid, only a relatively small proportion of the raft's volume needs to be immersed in the fluid in order to displace an equivalent mass of fluid.
If you were to assume pure ice floating in pure water, this method would give a raft thickness intermediate between the extremes you calculated in Question 10. Thus, the heights of the cliffs at the edges of rafts show with a fair degree of confidence that when the ice broke up to create the rafts its thickness was not less than a few hundred metres and not more than a few kilometres.
This is not necessarily the long-term ice thickness on Europa. Clearly, it is possible that the local heating event responsible for chaos generation might have melted quite a lot from the base of the continuous ice sheet before this finally broke up. On the other hand, the method we have used to calculate the thickness of the rafts relies on the ice of the re-frozen matrix being both thinner and weaker than the raft ice, at least until cooling-related thickening and ridge and groove development has turned the matrix into 'ball of string' terrain. So we can imagine regions of ice on Europa both thinner and thicker than the values you calculated in Question 10.
