1.2.1 The Pont du Gard: one of a kind
Bridging ditches, dips in the land, streams, rivers and roads is one obvious engineering task. Many of us will cross several bridges during a normal day, and there's sure to be one not far from where you live. You will be aware that there are many different designs of bridge, from little more than a beam across a gap to elegant suspension bridges.
For the makers of early bridges, such as the Pont du Gard, constructed around two millennia ago (Figure 2), the problem was that they were limited to materials like wood and stone. Metals, although in use for tools, armour and weapons, couldn't be produced in sufficient quantity or quality for bridge building until the nineteenth century.
Wood doesn't last too well, so let's turn our attention to stone. One of the problems with stone is that it is brittle : it is easily broken by an impact, and will tend to break rather than just deform. Stone is an example of a ceramic material (see Ceramics below). The pottery mugs you have at home are also ceramic, and they break easily if dropped onto a hard surface; a metal saucepan, on the other hand, would not break, though it might end up with a dent – metals tend to be tough.
When using stone, the trick is to ensure that it is used so that it is being compressed (see Compression and tension below). Think about the bricks used to make a house: they are stacked one on the other, so that each brick is compressed by those above it. This works fine. However, building a bridge is different from building a wall. It's impossible to make a stone bridge that is entirely compressed. So a way is required to minimise the areas that are in tension. The solution in the case of the Pont du Gard was to use arches: curved columns of stone which are compressed by the span of the bridge above them.
Ceramics
The term 'ceramic' covers a wide range of materials that are typically strong, hard and brittle. The minerals that make up rocks such as granite, sandstone and slate come into this category, as well as traditional pottery made from clay (the word ceramic comes from the Greek keramikos , meaning 'pottery') and manufactured rock-like construction materials including brick, cement and concrete.
Most ceramics have crystalline structures: they can withstand high temperatures and are resistant to chemical attack, which makes them useful for a wide range of applications. Glass, which also comes into this category, is unusual in having a relatively low melting point and a more random structure, but this gives it advantages in ease of processing and transparency. More recently a large number of advanced ceramics have been developed for a variety of specialist engineering applications.
Compression and tension
In construction particularly, and many other areas of engineering, the forces acting on the materials are critical to whether or not a structure will be safe. Materials have limits of strength which must not be exceeded.
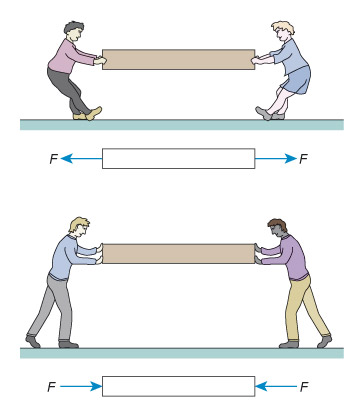
Forces are either compressive or tensile. You can think of compression as a 'squeezing' force, and tension as a 'pulling' force (see Figure 3). Modern structural materials (mainly metals) can withstand both tensile and compressive forces. Stone and similar ceramics are fine in compression, but their strength in tension is much lower.
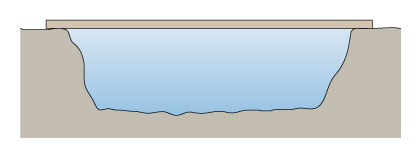
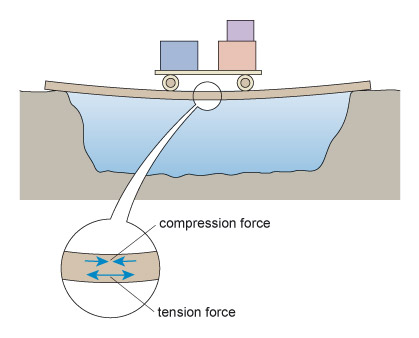
The simplest sort of bridge would be a slab over a ditch (Figure 4). When there is something on the bridge, it will bend – even if only very slightly. Bending puts tension onto the bottom of the slab, and compresses the top (Figure 5). So in building stone bridges, this tensile force must be minimised to below the level at which the slab would crack. This can be done either by making the slab shorter between its supports, or thicker thereby reducing the bending. Look how the design for the Pont du Gard has plenty of supports along its length, so that none of the stones will bend unduly. Forces due to bending crop up a lot in engineering: the simple act of walking across a room will bend the floorboards that support you.
Unlike most bridges, the Pont du Gard was not designed to carry people or animals, although tourists with a good head for heights can walk across it. It was built under the patronage of the Roman Emperor Agrippa in 18 BC to carry water to Nîmes in southern France. The water channel is nearly 50 m above the river, and traverses a distance of 270 m. The channel is nearly 2 m 2 in cross-sectional area and was lined with cement to make it waterproof. The arches, however, were all constructed of accurately cut stones using no cement at all.
With the Emperor backing the construction of the bridge, the financial side of the enterprise was presumably not a concern. But consider the necessary organisation of materials and labour. First it had to be decided exactly what was to be built. The design had to be worked out in meticulous detail so that the water channel would be at the correct height with the correct fall, so that the bridge would fit the site, and so that the stones could be cut to fit together to form the arches. The very existence of the bridge is proof that the Roman engineers had accurate methods of measuring and could transfer their calculations in instructions to the artisans (see Measuring sizes – length below). A quarry had to be established and means of bringing stone to the site provided: appropriate roads and carts. Workshops for preparing the stones to prescribed measures would most likely have been on site so that flexibility could be maintained during construction. Then there was a need for plenty of timber and skilled carpenters. Arches are built on a 'centring', which is a timber scaffold in the shape of the arch. Only when all the stones are in place for the whole curve of the arch can the centring be removed; the stones drop slightly and the arch becomes stable under its own weight. You will also realise that some heavy weights, both stones and timber, had to be shifted – which called for ropes, pulleys, levers …. And day by day the project had to be supervised, or kept on track, by an engineer who understood both what to do and how to do it. Evidently this engineer did it rather well: the result is still standing over 2000 years later.
Measuring sizes – length
The metric system was defined in France in the 1790s, following the French Revolution, to bring order to a confusion of vague and inaccurate standards. In fact the existing units were well defined – officially – but petty corruption and fraudulent trade made a new standard necessary.
The SI unit of length is the metre. The original intention was for it to be simply related to the size of the Earth. The distance from the North Pole to the equator along the meridian through Paris was to be ten million metres. This distance could be measured by astronomical methods using the official standards of the existing units. The result of this measurement was transferred onto a bar, made of an alloy which does not corrode and is very stable, as two scribed lines, now defined as one metre apart. The bar became the standard from which copies could be made for distribution.
To give you a rough idea of a metre, it is a big walking step – actually quite an exaggeratedly big step unless you are tall. Of course you can measure it more accurately using a ruler or a tape measure.
In practice we have need of both bigger and smaller units of length for measurement, so the metre is multiplied or divided by factors of ten. There are special names for these, and a selection is shown in Tables 1 and 2.
| Factor | Symbol | |
|---|---|---|
| deca metre | × 10 | |
| hecta metre | × 100 | |
| kilo metre | × 1000 | km |
| mega metre | × 1 000 000 | Mm |
| giga metre | × 1 000 000 000 | Gm |
Of these only the kilometre is in common use.
The prefixes shown in italic in the left column are common to all metric units to describe the multiplying factor to be applied to the base unit. By agreement, the Système International (SI) of units recognises factors going up or down in steps of one thousand, although below a thousand factors of ten are also recognised. Thus all the factors shown in Tables 1 and 2 are recognised by the Système International. Although in the UK we still tend to use the mile when discussing large distances, the standard measure in most other countries is the km. Other units such as the mm, µm and nm find extensive use in engineering measurement, as you will see.
| Factor | Symbol | |
|---|---|---|
| deci metre | × 1/10 | dm |
| centi metre | × 1/100 | cm |
| milli metre | × 1/1000 | mm |
| micro metre | × 1/1 000 000 | μm |
| nano metre | × 1/1 000 000 000 | nm |
To get some idea of scale, kilometres are useful for measuring place-to-place distances (e.g. London to Paris is 340 km). By definition of the metre it is 40 Mm around the Earth. It's about 400 Mm to the Moon, and 150 Gm to the Sun. On the small side, a UK 2 pence coin is about 2 mm thick. A micrometre (also colloquially called a micron) is almost as small as can be seen with a good optical microscope (a human hair is about 100 microns in diameter), and a nanometre is taking us towards the size of atoms. Nanotechnology is a rapidly growing field of engineering which deals with very tiny structures – from simple carbon nanotubes to complex protein-based molecular motors.
Activity 2 (example)
Which is the larger distance in each of the following pairs?
- a.2000 mm or 1.8 m
- b.1 mm or 1 km
Answer
- a.2000 mm is 2.000 m, which is larger than 1.8 m
- b.1 mm is 1/1000 m whereas 1 km is 1000 m, so the kilometre is larger.
Activity 3 (self-assessment)
- a.Which is the larger distance in each of the following pairs?
- i.50 cm or 0.45 m
- ii.100 μm or 0.1 mm
- b.In a photograph taken using a camera attachment with a particular microscope, features that are really 2 μm wide appear as 2 cm wide. What is the magnification? In other words, what factor does the lens multiply the 2 μm object size by in order to provide the 2 cm image size?
Answer
a.
- i.50 cm is 0.5 m, which is larger than 0.45 m.
- ii.100 μm and 0.1 mm are the same: 100 μm is 100 × 10−6, or 10−4m, and 0.1 mm is 0.1 × 10−3= 10−4m.
- b.The magnification is: