2.4 Bicycle structures
A bicycle consists essentially of a horizontal beam, to which is attached the wheels and a seat post. It is this beam which, structurally, is the most important part of the bicycle. There are forces acting on this beam when a cyclist simply sits on the machine, and they can be particularly large when the cyclist stands on the pedals going uphill, for example. This beam must provide stiffness for the bicycle: a wobbly bicycle isn't much use because the rider wants the downward force on a pedal to result in work that propels the bicycle forward, not into twisting and bending of the structure. A wobbly frame would also feel unstable to the rider. As has already been noted, the Brompton uses a low horizontal beam.
Many bicycles use a high beam, with diagonal posts to join this beam to the pedals and rear wheel in a twin triangle configuration known as a 'diamond frame' (Figure 24(a)). As we have discussed previously, what is required is a stiff structure that is as light as possible. The shape and size of the bars is critical as is the overall structure of the frame, for example the frame in Figure 24(a) being essentially a pair of triangles in a 'diamond' frame. The triangle is a potentially strong structure that is also light. Also, we have a choice of materials: aluminium, steel, or something more exotic such as carbon or titanium. Figure 24(b) shows a carbon-fibre composite bicycle. This material has a good stiffness with a low density (so low weight), and in addition the frame is designed to be particularly aerodynamically efficient. A bicycle similar to this, the Lotus Sport bike, was ridden by Chris Boardman when he shaved six seconds off the 4000 metres Individual Pursuit world record at the Olympic Games in Barcelona in 1992. This design represented a step-change innovation at the time; the implications are still being worked through in current designs.

A racing bicycle like that in Figure 24(b) is built regardless of cost and the suitability of the design for mass production. In our earlier terminology, it occupies a different design space from the folding bicycle, primarily because of the difference in function: to win races, rather than to be portable and affordable. Certainly such a bicycle has no requirement to be foldable. The frame of the Lotus Sport pursuit bicycle was moulded from woven sheets of aligned carbon fibre, layered in a mould with epoxy resin, which was then cured. It weighed 8.5 kg. Although the resulting composite has an excellent stiffness-to-weight ratio, weight is relatively unimportant in a pursuit race because only the first 125 m involve acceleration. The rest of the race takes place at a more or less constant speed – as fast as possible. So it is aerodynamic drag, which accounts for 96% of the total resistance to motion, that is the predominant design parameter for a pursuit bicycle. About one-third of the total drag is due to the bicycle.
However, the main criterion for the Brompton is foldability, with weight coming an important second; aerodynamics are not important at all. An ordinary bicycle weighs about 12 kg and is relatively easy to lift and use over short distances. Key components such as wheels, gears and handlebars are available in aluminium and are generally lightweight. The designs for these are mature and well optimised for the range of everyday uses.
Activity 12 (exploratory)
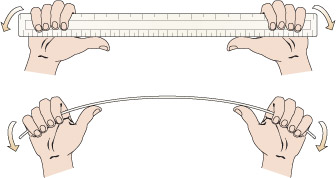
Find two rulers or long flat objects of similar sizes and thicknesses but made from different materials. Wood and plastic will do fine. I shall assume you have a wooden and a plastic ruler to hand, that they are the same length and have about the same cross-sectional dimensions – thickness and width. Approximately the same dimensions are required because you are going to look at differences between materials. Bend one of the rulers about both cross-sectional axes. You will find it very easy to bend one way, but not the other (Figure 25). From this you can observe that stiffness changes in different directions and according to where the loads are applied.
Having completed the experiment, answer the following:
- a.How would the ruler behave if it had a square cross-section.
- b.Which material was the stiffest when you bent the rulers?
Answer
- a.The ruler would bend the same extent in both directions, i.e. it is symmetrical.
- b.The wooden ruler is likely to be stiffer than the plastic one.