3.7 Looking at a standard: eye protectors
In many workplaces involved directly with manufacturing, there is the possibility of hazardous debris being flung around from various sources. Obvious examples are when components are being cut or otherwise machined, or if hot or toxic liquids are being handled.
A wide range of safety equipment is used in such environments. One of the most basic is for eye protection – that is, goggles or a visor to prevent any hazard from damaging the eyes of a worker (Figure 48).

Eye protection equipment is sufficiently important to have a standard dedicated to it (designated BS EN 166: BS means it is a British Standard, and EN means it is also applicable across Europe). This means that anyone purchasing protective eyewear, whether for a school chemistry laboratory or a production workshop, can check its label to see if the product conforms to this standard and, if so, be confident that it will indeed be suitable for the job for which it is intended.
Activity 20 (exploratory)
This activity introduces you to the standard BS EN 166:2002 (Personal eye-protection – Specifications), you can find part of this standard in the appendix to this course. Only extracts from the standard are provided here because the whole document is long and contains a lot of detail not needed here. However, read carefully Section 1 Scope and look at the headings to see what it contains.
- a.Is BS EN 166 applicable for the following products?
- i.A set of goggles worn by a welder.
- ii.Protective glasses worn by a worker at a nuclear reprocessing plant.
- iii.Sunglasses for use in cold weather.
- iv.Prescription glasses (i.e. glasses to correct for a vision problem like short-sightedness) supplied to a worker who operates a lathe.
- b.Is BS EN 166 the only standard in this field?
Answer
a.
- i.Yes, this is within the scope of the standard.
- ii.No, as the standard does not cover nuclear radiation.
- iii.No, it is indicated that sunglasses are covered by a separate standard.
- iv.Yes, this is covered by the standard, in the final paragraph of the 'Scope'
- b.No. The Scope indicates there are separate standards covering, for example, eye protectors for laser light.
Before we begin to examine BS EN 166 further, it would be useful to review Writing decimal numbers and Precision.
Writing decimal numbers
In the English-speaking world, fractional decimal numbers are conventionally written with a 'decimal point' after the whole number. So 2½ is written as 2.5. This is the notation that we have already used as the norm for this unit.
In some European countries, the decimal point is often replaced by a comma; so in this example 2.5 would be written as 2,5. Because BS EN 166 is a pan-European standard, the comma notations is used for decimal numbers where there is a figure after the decimal point.
Precision
It is not unusual in standards, or any other sort of engineering specification, to see a length quoted as something like: length = 20 mm ± 0.5 mm. The ± symbol is a combination of a plus and a minus sign, and is read as 'plus or minus'.
A specified length of, for example, 20 mm ± 0.5 mm (or (20 ± 0.5) mm) means that any length from 19.5 mm to 20.5 mm will meet the specification. The 'plus or minus' part of the specified length is sometimes called the tolerance. The part of the specification that comes before the tolerance is the nominal value. In this case the nominal value is 20 mm. Any dimensions, or other measurements, in a specification are likely to be given as a nominal value and a tolerance. There are at least two reasons for this:
- In practice, an exact nominal value is usually not required. For example, a range of sizes for a particular component may give perfectly satisfactory operation when the component is used in a machine. It is more useful to the manufacturer of the component to say what this range is than to stipulate an exact length without a tolerance.
- There would be no point stipulating an exact length anyway, since there is always a degree of uncertainty in any measurement. A manufacturer could never be certain that a component met the required specification if all that had been specified was a nominal value.
A tolerance of ± 0.5 mm on a nominal length of 20 mm would not be considered unusual in many undemanding applications. A tolerance of ± 2 mm on the same nominal length would be quite wide, as 2 mm is 10% of 20 mm. Sometimes the tolerance is not spread evenly on either side of the nominal value. For example, a particular speed might be given as:
This means that the speed can be faster than the nominal speed of 12 m s –1 by up to 0.6 m s –1 , but may not be less. This particular notation is fairly unusual, and you will not encounter it again in the course.
The BS EN 166 standard is quite broad in its coverage of the requirement for a set of eye protectors. Eye protectors might have to be exposed to flying objects, small particles, splashes of liquid metal, and flashes of light bright enough to cause blindness. All of these hazards are encompassed by the standard, although it is not necessary for a particular product to be safe against every single one of them.
The most important part of the eyewear is the ocular, which forms the lens of the protective eyewear; that is, the clear barrier in front of the eye. The physical strength or endurance of the ocular is defined in the standard by a criterion, aptly named as robustness. The test for robustness in the standard is as follows:
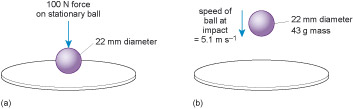
The requirement for minimum robustness is satisfied if the ocular withstands the application of a 22 mm nominal diameter steel ball with a force of (100 ± 2) N.
The above extract states the minimum robustness. There is also an enhanced robustness criterion. If the ocular is removed from the spectacle frame for testing, this criterion is:
The ocular shall withstand the impact of a 22 mm nominal diameter steel ball, of 43 g minimum mass, striking the ocular at a speed of approximately 5.1 m s −1.
In both cases, the ball must not penetrate the lens, and the lens must not fracture or be greatly deformed if the protectors are to pass the test. If the ball passes through the lens or the lens breaks, then clearly the protectors would not be doing their job. If the lenses are tested whilst mounted in their frames, then they must not be pushed out of the frame, even if they remain intact when doing so. Figure 49 illustrates the tests.
Activity 21 (self-assessment)
The volume, V , of a spherical object (a ball) is given by:
where r is the radius (which is half of the diameter) of the sphere (π see A fundamental constant (pi) ). The density of steel is 7800 kg m –3. Use this information to calculate the mass of the 22 mm diameter steel ball described above.
Answer
The volume of the ball is:
We can now use this to calculate the mass of the ball.
so
So you can see that a steel ball of the required diameter must have a mass of at least 43 g.
A fundamental constant (pi)
When dealing with circles and spheres, you will often see the symbol π cropping up. This is the Greek letter pi (pronounced pie ). It is used to represent the ratio between the circumference of a circle and its diameter. (The circumference of a circle is the distance you travel in one complete circuit of the edge of the circle.) The ratio of circumference/diameter is the same for every circle, and is about 3.14. This ratio is called π, and its exact value is impossible to determine because the decimal part of the number is infinitely long. It has been calculated to some millions of decimal places, and still it keeps going. However, for our purposes, the value of 3.14 for π is adequate.
Activity 22 (self-assessment)
Imagine you are going to test a spectacle lens against BS EN 166 for:
- a.minimum robustness
- b.enhanced robustness.
What quantities must you be able to measure accurately for each of these two sets of tests?
Answer
- a.For minimum robustness, it is necessary to know the ball's diameter and the force used to press it into the ocular.
- b.For enhanced robustness, rather than measuring force, it is necessary to measure speed, which, as we shall see, is actually done by measuring the height from which the ball is dropped.
From the introduction to this standard, and the answer to Activity 22, we can see that whilst any individual standard may appear self-contained, there is often subsidiary information that is needed by a manufacturer. BS EN 166 does not indicate how the measurements are to be performed, only what the requirements are. If the protective glasses are fitted with prescription lenses there are different standards that also need to be taken into account. In fact, the specifications for robustness given above specify that the test methods should be in accordance with the method given in another standard, BS EN 168. So, in addition to a standard on the requirements for protective lenses, there is also a standard that gives information on how the tests can be carried out for these requirements. One of the reasons for having standards is that they provide a way of disseminating advice and information on how to complete basic measurements, or use a particular product in a certain application.
Section 2: Normative references in BS EN 166 indicates other standards that are related to this one. Some of the related standards contain test methods (such as Personal eye protection – Non-optical test methods ); others cover eye protection for more specific use, such as for sun-glare filters. It soon becomes clear that no standard exists in isolation. The list of standards relating to eye protection is a good example. The standards for personal eye protection differ from those for spectacle lenses, and differ from those relating to protection from strong light sources – whether this is the sun or an artificial source of radiation (see Radiation, light and the visible spectrum ).
Activity 23 (self-assessment)
What are the units of π (pi)?
Answer
The ratio π is calculated by dividing circumference (a length) by diameter (another length). So these units cancel each other. Thus π has no units: it is just a number.
Radiation, light and the visible spectrum
In everyday speech, the word radiation is usually taken to mean the harmful emissions from radioactive material. However, in its correct scientific usage, radiation refers to various types of emission, only some of which are related to radioactivity, and only some of which are harmful. One of the commonest types of radiation is electromagnetic radiation, which is itself an entire spectrum of kinds of radiation, including for example light, microwaves, X-rays and some forms of damaging radioactivity. All varieties of electromagnetic radiation have the same fundamental nature, which is what the term 'electromagnetic' refers to. (Electromagnetic radiation is distinguished from particle radiation, which has a different nature.) We can use the example of light to illustrate properties that are common to all electromagnetic radiation.
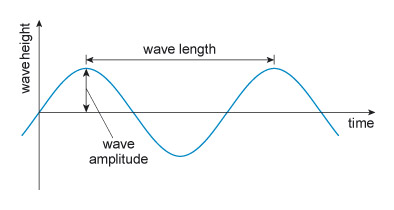
In simple terms, light can be envisaged as travelling as a wave, rather like the way the ripples in a pond travel out from their source. The distance between the peaks of the waves (Figure 50) is known as the wave length , or just wavelength.
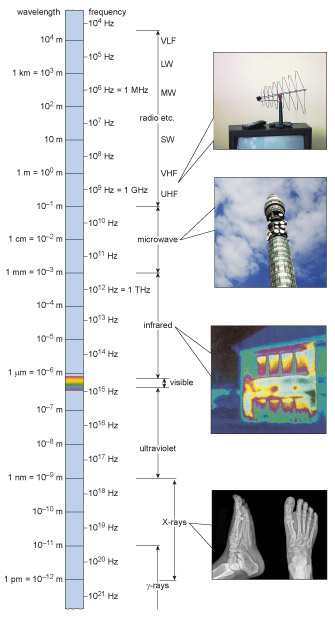
Wavelength can vary enormously, and as the wavelength changes so the properties of the radiation change. Since we classify various forms of electromagnetic radiation by their properties, the wavelength provides a useful way of specifying particular types of electromagnetic radiation. Figure 51 shows the electromagnetic spectrum. You can see that it ranges from gamma rays (one of the harmful types of radiation) at very short wavelength, through to radio waves at long wavelengths. Visible light comes somewhere in between. Here we see the use of a logarithmic scale for plotting data: the wavelengths shown on this figure range from 10 –13 m at the gamma-ray end (equivalent to a tenth of a thousandth of a billionth of a metre) to 10 6 m (one thousand kilometres) at the radio wave end.
Another useful way of characterising electromagnetic radiation (or any other wave phenomenon, such as sound) is by its frequency. This is the number of waves that pass a stationary point each second, measured by counting the peaks per second. Although frequency is a simple concept – a number per second – it is given its own unit, the hertz, abbreviated to Hz. A frequency of 10 Hz is ten complete waves per second.
Activity 24 (self-assessment)
From Figure 51:
- a.What is the approximate wavelength of visible light?
- b.What is the frequency of microwaves?
Answer
- a.Visible light falls in the range of wavelengths between 10 –6 m and 10 –7 m, and is typically 400–700 x 10 –9 m or 400–700 nm.
- b.Microwaves have a frequency between about 3 x 10 9 Hz and 3 x 10 11 Hz.
Let's now investigate the detailed procedure for the increased robustness test. BS EN 166 specifies that the test ball must strike the ocular with a certain speed: around 5.1 m s –1 (Figure 49). The standard also indicates that dropping the ball from a height of 1.3 m will provide this speed.
Of course the standard makes the assumption that the test is carried out on Earth, and that you haven't done something bizarre like cover the test rig in treacle! Gravity produces a force on everything at the Earth's surface, and when something is dropped this force causes the object to accelerate. You may also remember that the acceleration due to gravity is 9.8 m s –2.
Activity 25 (self-assessment)
If an object is dropped on Earth from rest, how fast will it be travelling:
- a.after 1 second?
- b.after 5 seconds?
Answer
Under Earth's gravity, an object will accelerate at 9.8 metres per second per second.
- a.After one second, it will be travelling at 9.8 m s –1. It's as easy as that!
- b.Every second, the object will speed up by a further 9.8 m s –1 , so after 5 seconds it will be travelling at (5 × 9.8) m s –1 = 49 m s –1. The velocity is simply the acceleration multiplied by the time for which it acts.
Activity 25 shows it is possible to calculate how fast an object would be travelling after it had been accelerating for a certain length of time. We can also calculate how fast an object would be travelling after it had been accelerating over a certain distance.
If we use symbols to represent speeds, acceleration and distance, we can make this relationship easier to write. If there is an acceleration a over a distance s , then something that starts with a speed of u will end up with a speed of v. The mathematical derivation of the relationship between all these is outside the scope of this course, but the answer turns out to be:
v2 = u2 + 2as
Thus if we know u , the starting speed of the object at a moment in time, we can work out what the final speed v will be after an accelerating or decelerating force acts upon it over the distance s.
In the case of a ball which is dropped, there is zero initial speed, so our equation becomes:
- v2 = 2as
which, if we take square roots of each side, can also be written as:
The term v is the final speed after the object has moved through the distance s (fallen this distance in the case of an object being dropped). The term a represents the acceleration that it experiences. Properly speaking, a represents the magnitude of the acceleration. You will recall that acceleration is a vector, and therefore incorporates both a magnitude and a direction. The above equation takes no account of the direction of the acceleration.
Activity 26 (self-assessment)
Confirm that a ball dropped from a height of 1.3 m will be travelling with a speed of 5.1 m s –1 when it hits the surface below if air resistance is ignored.
Answer
Using the equation
we find that:
This is just less than the 5.1 m s –1 expected.
Fortunately we have been able to use a bit of fundamental physics here to help us establish the speed of the ball – the fact that a ball dropped under Earth's gravity accelerates at a certain rate. If we had needed to measure the speed of the ball directly in order to prove that the test conditions were correct, it would have involved complicated and probably expensive equipment, all of which would have added to the final cost of the product. One of the key points that I want to convey here is that measurement methods are important. We have discussed already how the units of measurement are critical in ensuring compatibility of data. The way in which the measurements are made, in order to find values for specific quantities, is equally critical. This is why the eye protection standard has related standards concerned solely with the test methods.
You may have noticed, if you have looked at the standard, that impact resistance is not the only protection offered by eye protectors. They can also give protection against dust, and splashes of liquid metal, for example. Each of these elements of protection is tested in a particular way.
The consequence of all this is that as long as the conditions of the test, which are specified by the standard, are adhered to, the results for a particular make of eye protector should be the same no matter where the test is conducted. The fact that there is a standard for the test method as well as for the specific criteria for the protectors indicates the importance of the testing method. Without standardisation of this kind, it would be possible for manufacturers to claim that their product offered superior protection, whilst using non-rigorous testing methods to define their performance. As it is, eye protectors which conform to BS EN 166 will be labelled as having conformed to the relevant requirements.
Activity 27 (self-assessment)
A new apparatus for firing ball bearings horizontally has been developed for testing the lenses of eye protectors. The balls are accelerated at a rate of 80 m s –2 for 0.1 s, and then travel 2 m before hitting the lens. While they are travelling, there is a deceleration (a negative acceleration) of 6 m s –2 owing to air resistance. What will the horizontal velocity of the ball be when it reaches the lens? Is this consistent with the requirements of BS EN 166?
Answer
The ball is accelerated at 80 m s –2 for 0.1 s. The speed after this acceleration is just the acceleration multiplied by the time, so the speed will be:
The ball then slows down as it travels towards the lens. The final horizontal velocity can be derived from:
That is,
Note that the acceleration must be written as a negative number here, as the ball is being slowed by the air resistance.
This is above the speed recommended by the standard, so the test, although possibly more stringent than the requirements, would not conform. The machine could be adjusted to provide the correct speed.
This section has introduced you to the sorts of requirement that are aimed at in a standard for a particular product. The case we have examined, the standard for eye protectors, gives specific tests that the product must pass before it can claim to conform to the standard. This is typical of a standard for a product or a range of products. Such standards tend to define the function and performance of the product, and there may be tests the manufacturers must apply, or certain ranges of dimensions like length or weight, which the product must comply with.
This is just one type of standard. Examples of other types of standards are those dedicated to testing methods, and standards for processes or practices.