1.1 Modelling motion with perpendicular vectors
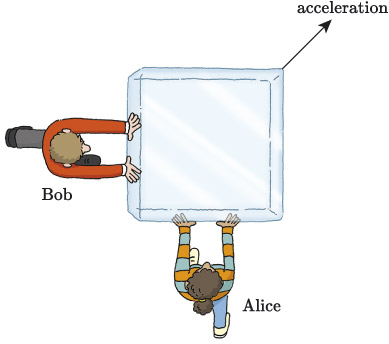
Let’s consider, where two people, Alice and Bob, are pushing a block of ice, which has a mass of a metric tonne (). Alice and Bob each push on a different face of the block, as illustrated in Figure 3, and the direction in which the block moves is a consequence of the combination of the forces they apply. If Bob applies a force of 130 N to the left face of the block, and Alice applies a force of 110 N to the bottom face, what is the combined force applied to the block, and what is the acceleration of the block?
1.1.2 Calculating the magnitude of a combined force
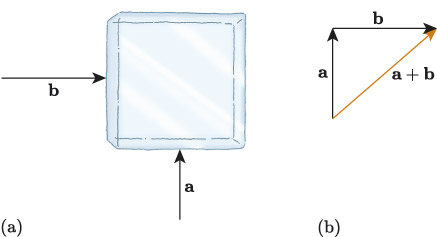
The net effect of these two forces by combining them visually using arrows, as illustrated in Figure 4. Figure 4(a) shows an abstraction of the drawing in Figure 3, with Alice and Bob replaced by arrows representing the forces applied by Alice and Bob to the block of ice. Here, represents the force applied by Alice, who is below the block, and represents the force applied by Bob, who is to the left of the block. Notice that the vectors are shown to be acting on the centres of the faces of the block. This is because if forces are applied away from the centres, this can create a rotation, and that is a more complicated situation to model. Such rotational effects are outside the scope of this module.
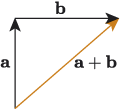
Figure 4(b) shows the result of visually adding the vectors and . . In this example, and are perpendicular, so the triangle formed by , and the resultant is a right-angled triangle, with as the hypotenuse. So we can use Pythagoras’ theorem to find the magnitude of , written , from the magnitudes of and , written and .
Activity 1
If is a positive vertical vector that has magnitude 110 N and is a positive horizontal vector that has magnitude 130 N, what is the magnitude of the resultant to two decimal places?
1.1.3 Calculating direction of motion of a combined force
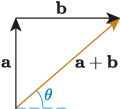
Using the fact that , and the resultant form a right-angled triangle, we can also use trigonometric functions to find the direction of . This is illustrated in Figure 4.5, where the direction of is represented by the angle . But is outside the triangle formed by , and , so we can’t directly calculate its size using trigonometry; we also need to use our knowledge of angles and triangles.
In particular, we can use the properties of angles on lines, as summarised here.
Opposite, corresponding and alternate angles
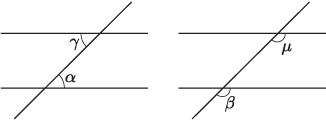
Where two lines intersect, opposite angles are equal. This is commonly referred to as the X-angles rule. For example, in the following diagram, .

Where a line intersects parallel lines:
- Alternate angles are equal. This is commonly referred to as the Z-angles rule. For example, in the diagram below, .
- Corresponding angles are equal. This is commonly referred to as the F-angles rule. For example, in the diagram below, .
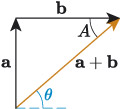
For example, to find the angle in Figure 5, we can use alternate angles (Z-angles). So in Figure 6, angles and are equal, and to find we use trigonometry, e.g. the tangent function.
Activity 2
In Figure 6, if is a positive vertical vector that has magnitude 110 N and is a positive horizontal vector that has magnitude 130 N, what is the direction of the resultant to one decimal place? Use the fact that and are alternate angles to help you.
1.1.4 Calculating acceleration from a combined force
With the magnitude and direction of the resultant vector now calculated, we can use Newton’s second law to determine the acceleration of the block. Recall that Newton’s second law states that
The block has a mass of a metric tonne () and because it is made of ice we will ignore any forces due to friction. The force applied by Alice and Bob is , which has the magnitude calculated in Activity 1 and the direction calculated in Activity 2.
Example 1 Finding acceleration from a combined force
A block of ice has a mass of a metric tonne (). If Bob applies a force of 130 N to the left face of the block while Alice applies a force of 110 N to the bottom face, what is the acceleration of the block? Give the magnitude of the acceleration to two decimal places and the angle to one decimal place.
Solution
Newton’s second law gives us
so acceleration is given by
In the following calculations we will use the vector to represent acceleration, to avoid confusion with the vector which is the force applied by Alice. The mass of the block of ice is and, when we ignore friction, the only force acting on the block is the resultant force due to Alice and Bob pushing the block, so
and the acceleration of the block is given by
Multiplying a vector by a positive scalar does not change the direction of the vector, so the direction of the acceleration is the same as the direction of , and is given by (to 1 d.p.).
We also know that when multiplying a vector by a positive scalar, its magnitude is changed through multiplication. So, the magnitude of the acceleration is
So, the block accelerates at (to 2 d.p.) in a direction that is (to 1 d.p.) from the positive horizontal direction.