2.3 Converting between vector forms

It is useful to be able to convert between the different forms of vectors, so that we can make use of the form that is most appropriate for a given situation. For example, the vector in Figure 18(a) represents the displacement of London from Milton Keynes, and direction and angle are the most intuitive description for this vector. London is approximately 65 km south-east of Milton Keynes. Similarly, the vector in Figure 18(b) represents the motion of an aircraft, and for describing the ground speed of the aircraft, a description of the vector in terms of horizontal and vertical components is required.

Figure 18 Examples of vectors: (a) displacement of London from Milton Keynes; (b) motion of an aircraft

Show description|Hide description

18(a): An example of a vector. The route from Milton Keynes to London is displayed on a map and can be thought of as a vector between two points.

18(b): The flight of a zeplin as defined by the vertical vector keeping it afloat, a horizontal vector as it flies through the sky and the resultant vector.

Figure 18 Examples of vectors: (a) displacement of London from Milton Keynes; (b) motion of an aircraft

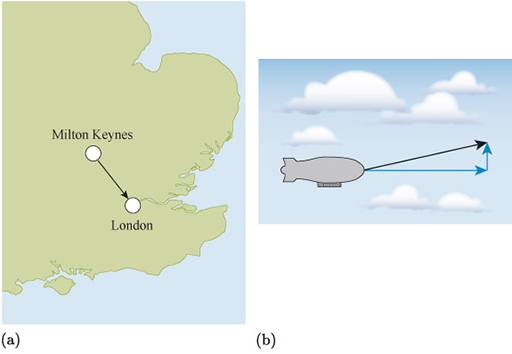
In both situations it is useful to be able to convert between vector forms. For example, it may be necessary to describe how far east London is from Milton Keynes, and how far south. To describe the direction in which the aircraft is flying, it is useful to use the resultant velocity.

The mathematics that allows us to convert between different forms of vectors.

Figure 19 A vector and its components

Show description|Hide description

A vector v and its components. Vector v is at an angle θ from the horizontal component and is made up of the horizontal component |v| cosθi and the horizontal component |v| sinθj.

Figure 19 A vector and its components

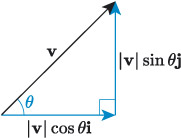
We have already identified how to calculate the magnitude of the component vectors of a vector. For example, the vector in Figure 19 has magnitude and direction , and its components are defined as and .

Putting these into component form we have the following result.

Figure 20 A vector

Show description|Hide description

A vector v at an angle θ to the horizontal component and is written as the sum of two vectors, ai and bj, so that v=ai+bj.

Figure 20 A vector MathJax failure: MathML - Unexpected text node: '

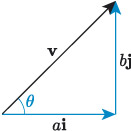
Going the other way, to find the magnitude and direction of a vector from its component form, the reasoning is the same as how to convert between Cartesian and polar coordinates. For example, the vector illustrated in Figure 20 has horizontal component of magnitude and vertical component of magnitude , and in component form is given by . To calculate the magnitude of , we can use Pythagoras’ theorem, and to calculate the angle , we can use the inverse tangent function.

Remember, when using the inverse tan function, care must be taken to ensure that the answer given by a calculator is correct.