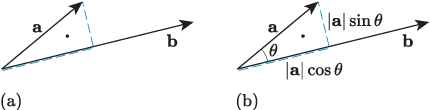4.2 Scalar product of a vector from magnitude and direction

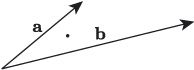
Another way to consider the scalar product is to consider how it is defined in terms of the magnitudes and directions of two vectors. Consider again the vectors and in Figure 29. We want to find out how much vector will grow vector . So again we want to identify how much the vectors interact – and one way to do this is to determine how much vector points in the direction of vector .

Figure 31 Finding the scalar product of and by comparing magnitudes and directions

Show description|Hide description

Finding the scalar product of two vectors, a and b by comparing the magnitude and the direction.

Figure 31 Finding the scalar product of MathJax failure: MathML - Unexpected text node: '

In Figure 31, the vectors are arranged so that their tails meet, and this makes it possible to compare their magnitudes and directions. To make this explicit, we can draw the components of , not in terms of horizontal and vertical directions, but in terms of the direction where  is pointing, as illustrated in Figure 32(a). Formally, the component of  that points in the direction of  is called the projection of  onto , and if the angle between and  is , then the length of the projection of  onto  is , as shown in Figure 32(b).

Figure 32 Projecting onto

Show description|Hide description

32(a): Projecting a onto b.

32(b): The angle between a and b is denoted by θ so that a has perpendicular components |a| cosθ and |a| sinθ

Figure 32 Projecting MathJax failure: MathML - Unexpected text node: '

Comparing the components of  with  will give us a measure of how much  and  interact, as illustrated in Figure 33. In the direction of , has a component of magnitude , and  has a component of magnitude , so the contribution to the value of is . Perpendicular to ,  has a component of magnitude , and  has a component of magnitude 0, so the contribution to the value of is 0.

Figure 33 Interacting component vectors in the scalar product of and

Show description|Hide description

Interacting component vectors in the scalar product of a and b. Left: If a and b are parallel vectors then the scalar product is given by |a| cosθ · |b|. Right: If a and b are perpendicular, the scalar product is zero.

Figure 33 Interacting component vectors in the scalar product of MathJax failure: MathML - Unexpected text node: '

So

and this is a measure of how much the scalar quantity grows the scalar quantity .

and are parallel, so

and the scalar product is given by

Scalar product of vectors in terms of magnitude and direction

The scalar product of two vectors and is

where is the angle between and .

Activity 20

Suppose that , and are vectors with magnitudes 4, 3 and 2 respectively, and directions as shown in the following figure.

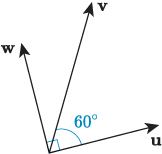
Find the following scalar products.

• a.

• b.

• c.